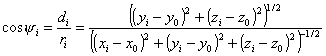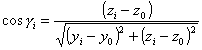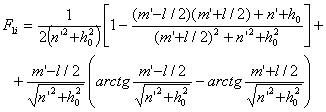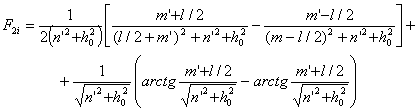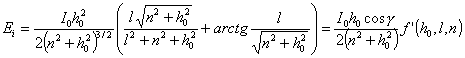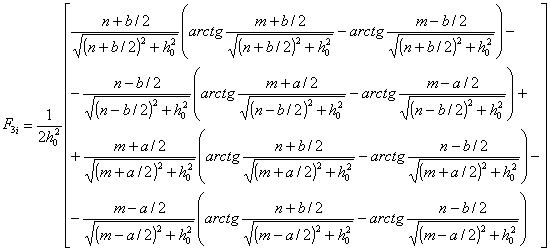РАГС - РОССИЙСКИЙ АРХИВ ГОСУДАРСТВЕННЫХ СТАНДАРТОВ, а также строительных норм и правил (СНиП)
и образцов юридических документов
Произвольная ссылка:
Пособие к МГСН 2.06-99 Расчет и проектирование искусственного освещения помещений общественных зданий.
ПРАВИТЕЛЬСТВО МОСКВЫ
МОСКОМАРХИТЕКТУРА
ПОСОБИЕ
к МГСН 2.06-99
расчет и проектирование
искусственного освещения
помещений общественных зданий
1999
ПРЕДИСЛОВИЕ
1. Разработано: Научно-исследовательским институтом строительной физики (НИИСФ) Российской академии архитектуры и строительных наук (РААСН) (к.т.н. Шмаров И.А., инж. Котлярова Н.И., к.т.н. Козлов В.А., инж. Исхакова Г.Р.); Обществом с ограниченной ответственностью «Всероссийским научно-исследовательским и проектно-конструкторским светотехническим институтом» (ООО «ВНИСИ») (д.т.н, проф. Айзенберг Ю.Б., к.т.н. Федюкина Г.В.); Товариществом с ограниченной ответственностью «Церера» (Орлов А.В.)
2. Подготовлено к утверждению и изданию Управлением перспективного проектирования и нормативов Москомархитектуры (инж. Щипанов Ю.Б., инж. Ионин В.А.)
3. Утверждено указанием Москомархитектуры от 28.10.99 № 43
СОДЕРЖАНИЕ
1. РАСЧЕТ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
1.1. Выбор метода расчета
1.1.1. Все применяемые методы расчета освещения можно свести к двум основным: точечному и методу светового потока, подразделяющемуся на метод коэффициента использования и метод удельной мощности.
В принципе, оба метода равноправны, области их применения в значительной степени пересекаются, но между ними есть существенные различия.
Точечный метод в основном предназначен для нахождения освещенности в точках, и, следовательно, он наиболее пригоден для расчета минимальной освещенности, регламентируемой нормами для большинства освещаемых объектов.
Метод коэффициента использования предназначен для определения средней освещенности и при расчете этим методом минимальная освещенность оценивается лишь приближенно, без выявления точек, в которых она имеет место. Средняя освещенность может быть рассчитана на как угодно расположенной поверхности, но наиболее употребительные формы этого метода предназначены для расчета только горизонтальной освещенности.
1.1.2. Точечный метод является предпочтительным к использованию и незаменим в случаях:
- необходимости учитывать возможные затенения;
- предъявления требований к равномерности распределения освещенности;
- определения освещенности наклонных поверхностей.
Применение точечного метода целесообразно для расчета осветительных установок (ОУ) с повышенной неравномерностью распределения освещенности (локализованное освещение светильниками прямого света, наружное освещение, рассчитываемое на минимальную освещенность, аварийное освещение и т.п.), а также для расчета освещения наклонных поверхностей, создаваемого светильниками прямого света.
1.1.3. Метод коэффициента использования целесообразен во всех случаях, когда расчет ведется по средней освещенности и, в частности, для расчета общего равномерного освещения.
1.1.4. Общее равномерное освещение помещений может быть рассчитано любым методом. Однако в ответственных случаях предпочтение следует отдавать точечному методу, так как он позволяет проанализировать распределение освещенности по площади помещения. При использовании светильников концентрированного светораспределения необходимо применять только точечный метод.
1.1.5. Имеются случаи, в которых ни один из указанных методов расчета в отдельности не дает точных результатов. К таковым относится расчет локализованного освещения или освещения наклонных поверхностей в помещениях, освещаемых светильниками, не относящихся к классу прямого света. В этих случаях прямую составляющую освещенности определяют точечным методом, а дополнительную отраженную - методом коэффициента использования.
1.2. Общие положения при расчете освещенности
1.2.1. Расчет искусственного освещения заключается в определении числа и мощности источников света, обеспечивающих нормированную (с учетом коэффициентов запаса) освещенность, либо в определении по заданному размещению светильников и мощности источников света, используемых в них, создаваемой ими освещенности на указанных в нормах рабочих поверхностях.
1.2.2. Освещенность Ер.п. на рабочей поверхности создается световым потоком, поступающим непосредственно от светильников (прямая составляющая освещенности Еп.с. и отраженным, падающим на расчетную поверхность в результате многократных отражений от стен, потолка, пола, оборудования (отраженная составляющая освещенности Ео.с.):
Ер.п. = Еп.с. + Ео.с.,
1.2.3. Прямая составляющая освещенности рассчитывается на основе кривой силы света светильника и расположения светильников относительно выбранной точки на рабочей поверхности и поэтому ее значения на отдельных участках рабочей поверхности могут быть различными.
1.2.4. Отраженная составляющая освещенности определяется световым потоком, падающим на отражающие поверхности непосредственно от светильников, т.е. определяется светораспределением светильников, отражающими свойствами ограждающих поверхностей, а также соотношением размеров освещаемого помещения.
1.2.5. Методика расчета прямой составляющей освещенности выбирается в зависимости от применяемых, в дальнейшем именуемых как излучатели, светящих элементов проектируемой осветительной установки. В зависимости от соотношения размеров излучателей и расстояний их до освещаемой поверхности все разновидности излучателей можно разделить на три группы: точечные, линейные и поверхностные.
Точечность светящего элемента определяется его относительными размерами по отношению к расстоянию до освещаемой точки пространства. Практически принято считать светящее тело точечным, если его размеры не превышают 0,2 расстояния до освещаемой точки.
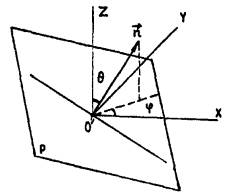
В практике расчета точечный светильник принимается за светящую точку с условно выбранным световым центром, характеризуемым силой света по всем направлениям в пространстве (рис. 1.1).
К точечным светящим элементам относятся прожекторы, светильники с ЛН и газоразрядными лампами типов ДРЛ, ДРИ, НЛВД, НЛНД и т.п.
Рис. 1.1. Ориентация расчетной плоскости Р в пространстве в сферической системе координат
1.2.6. К линейным светящим элементам относятся светящие элементы, имеющие несоизмеримо малые размеры по одной из осей по сравнению с размерами по другой оси.
В практике расчета к светящим линиям относятся излучатели, длина которых превышает половину расчетной высоты hр. К светящим линиям относятся люминесцентные светильники, расположенные непрерывными линиями или линиями с разрывами, а также протяженные светящие панели, длина которых соизмерима с расстоянием до освещаемой поверхности. Основной характеристикой линейных источников является удельная сила света, под которой понимают силу света, излучаемую единицей длины источника (1 м) в плоскости, перпендикулярной его оси, и кривые силы света в продольной и поперечной плоскостях.
1.2.7. К поверхностным излучателям, для которых нельзя применить закон квадратов расстояний из-за значительной погрешности, возникающей в расчете, относятся установки отраженного света в виде световых потолков или ниш; панели, перекрытые рассеивателями или экранирующими решетками. Размеры этих светящих элементов соизмеримы с расстоянием до расчетной точки. Светящие элементы этой группы характеризуются следующими показателями: формой и размером светящей поверхности, распределением яркости по различным направлениям пространства и по самой светящей поверхности. Световые потолки в установках отраженного света, а также световые потолки и панели, перекрытые рассеивателями, обладают практически одинаковой яркостью по всем направлениям пространства. Исключение составляют светящие поверхности, перекрытые экранирующими решетками, защитный угол которых может существенно влиять на распределение яркости в пространстве. При расчете осветительных установок этого типа можно принимать яркость светящей поверхности, равной ее среднему значению.
Использование поверхностных излучателей, требующих значительной установленной мощности, может быть оправданным в установках архитектурного освещения, когда кроме утилитарных требований, предъявляются также дополнительные архитектурно-художественные требования.
1.2.8. Необходимо иметь в виду, что в зависимости от условий применения излучатель может быть отнесен к определенной группе. Так, линейный излучатель может рассматриваться как точечный, если его длина в два раза меньше расстояния до точки, в которой определяется создаваемая им освещенность, при этом погрешность при расчете не превышает 5%. Аналогичное допущение может быть принято для поверхностного излучателя, если расстояние, на котором определяется освещенность, в 2,5 раза превышает наибольший размер поверхности.
Подход к расчету отраженной составляющей является общим для всех трех групп излучателей, он заключается в определении первоначально попавшего от светильников светового потока на отражающие поверхности ограждающих помещение конструкций.
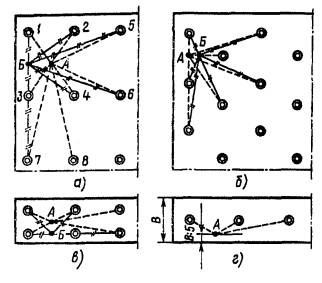
1.2.9. Характерные точки расчета для общего равномерного освещения показаны на рис. 1.2.
В принципе не следует выискивать точки абсолютного минимума освещенности у стен или в углах: если в подобных точках есть рабочие места, то доведение в них освещенности до требуемого значения может быть осуществлено увеличением мощности ближайших светильников или установкой дополнительных светильников.
Рис. 1.2. Расчетные точки освещенности
1.3. Светотехнические характеристики светильников. Кривые силы света светильников
1.3.1. В практике расчетов светильник принимается за излучатель (точку, линию, поверхность) с условно выбранным световым центром.
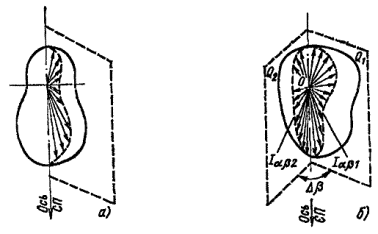
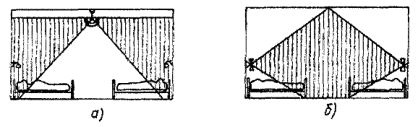
Светораспределение светильников определяется фотометрическим телом светильника, под которым понимается геометрическое место концов радиус-векторов, выходящих из светового центра, длина которых пропорциональна силе света светильника в соответствующем направлении (рис. 1.3).
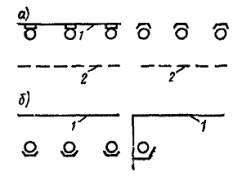
Рис. 1.3. Симметричные (а) и несимметричные (б) фотометрические тела световых приборов
Светораспределение светильников принято характеризовать кривыми силы света, представляющими зависимости силы света светильника от меридиональных a и экваториальных b углов, получаемых сечением фотометрического тела плоскостями. Преимущественно пользуются кривыми силы света I = I(a), получающимися сечением фотометрического тела вертикальными плоскостями при разных значениях углов b.
В зависимости от формы фотометрического тела светильника светильники подразделяются на симметричные, фотометрическое тело которых имеет ось или плоскость симметрии, и несимметричные (рис. 1.3). К первой группе относятся круглосимметричные светильники, кривая силы света которых одинакова при любых значениях углов b.
Кривые силы света представляются в виде графиков, таблиц или задаются в виде формул, аппроксимирующих кривые силы света.
Для светильников с симметричным фотометрическим телом ГОСТом 17677-82 «Светильники. Общие технические условия» кривые силы света представлены в виде графиков Ia = f(a) для светового потока светильника Ф = 1000 лм. По ГОСТ все светильники по типу кривой силы света подразделяют на семь классов: К, Г, Д, Л, Ш, М, С. Кроме того по типу светораспределения (доли излучения в верхнюю и нижнюю полусферы) светильники подразделяются на пять классов: П, Н, Р, В, О. Заводы-изготовители в паспортных данных на светильники указывают класс светораспределения и класс кривой силы света. Светильники отличные от данной классификации, считаются специальными, и на них указываются табличные или графические особые данные для характеристики светораспределения.
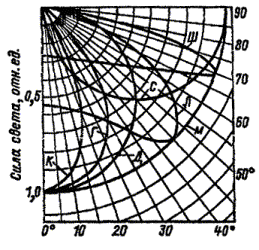
Отдельные стандартные классы светораспределения были детализованы (Д-1, Д-2; Г-1 ¸ Г-4; К-1 ¸ К-4; Л; Ш) и установлены поля допусков, в пределах которых реальное светораспределение светильника позволяет отнести его к тому или иному классу (рис. 1.4, табл. 1.3.1).
Рис. 1.4. Типовые кривые силы света по ГОСТ 17677-82 в относительных единицах
Таблица 1.3.1
ТИПОВЫЕ КРИВЫЕ СИЛЫ СВЕТА ОТЕЧЕСТВЕННЫХ КРУГЛОСИММЕТРИЧНЫХ СВЕТИЛЬНИКОВ (Ф = 1000 лм)
|
Ia = const |
Ia = I0 cos(na) |
Ia = I0 sin(na) |
Ia = I0 {cos(na)/cos[qsinm(Ca)]} |
||||||||||||||
|
- |
n=0,7841 |
n=1 |
n=1,0374 |
n=1,1038 |
n=1,2928 |
n=1,5109 |
n=1,65 |
n=1,7582 |
n=2,0402 |
n=2,3683 |
n=2,7471 |
n=2,91 |
n=1 |
q=70°; m=1,2; n=1,66 |
q=78,3°; m=1,4; n=1,39 |
q=84,4°; m=1,5; n=1,2 |
|
|
a, градусы |
м |
Д-1 |
Д |
Д-2 |
Д-3 |
Г-1 |
Г-2 |
Г |
Г-3 |
К-1 |
К-2 |
К-3 |
К |
С |
Л (Ш1) |
Л-Ш (Ш 2) |
Ш (Ш3) |
|
0 |
159,2 |
233,4 |
330,0 |
295,0 |
377,3 |
503,0 |
670,7 |
800,0 |
894,2 |
1192 |
1583 |
2120 |
2400 |
0 |
154,8 |
119,6 |
78,3 |
|
5 |
159,2 |
232,9 |
328,7 |
293,8 |
375,5 |
499,8 |
664,8 |
791,7 |
883,8 |
1173 |
1549 |
2062 |
2323 |
17,9 |
155,5 |
119,0 |
78,6 |
|
10 |
159,2 |
229,2 |
325,0 |
290,2 |
370,3 |
490,2 |
647,5 |
767,1 |
852,5 |
1118 |
1449 |
1893 |
2097 |
35,6 |
158,2 |
118,6 |
79,4 |
|
15 |
159,2 |
228,5 |
318,8 |
284,2 |
361,6 |
474,4 |
618,5 |
726,5 |
801,1 |
1026 |
1288 |
1595 |
1737 |
53,1 |
164,5 |
120,2 |
81,4 |
|
20 |
159,2 |
224,7 |
310,1 |
275,9 |
349,8 |
452,7 |
579,5 |
670,9 |
731,2 |
902 |
1052 |
1261 |
1265 |
70,1 |
175,5 |
126,0 |
81,7 |
|
25 |
159,2 |
220,0 |
299,1 |
265,3 |
334,3 |
425,1 |
530,2 |
601,5 |
643,8 |
750 |
810 |
832 |
712 |
86,6 |
190,7 |
134,0 |
83,3 |
|
30 |
159,2 |
214,1 |
285,8 |
252,5 |
316,0 |
392,1 |
471,4 |
519,6 |
541,3 |
574 |
515 |
249 |
113 |
102,5 |
210,8 |
145,0 |
87,2 |
|
35 |
159,2 |
207,1 |
270,3 |
237,7 |
294,7 |
354,1 |
404,7 |
426,9 |
439,9 |
380 |
196 |
0 |
0 |
117,6 |
235,1 |
159,6 |
94,8 |
|
40 |
159,2 |
199,3 |
252,8 |
221,0 |
270,7 |
311,7 |
330,9 |
325,4 |
301,0 |
174 |
0 |
0 |
0 |
131,8 |
261,8 |
180,4 |
105,4 |
|
45 |
159,2 |
190,6 |
233,3 |
202,4 |
244,2 |
265,3 |
251,4 |
217,2 |
168,8 |
0 |
0 |
0 |
0 |
145,0 |
281,6 |
209,7 |
121,3 |
|
50 |
159,2 |
180,0 |
212,1 |
182,1 |
215,4 |
215,5 |
167,3 |
104,4 |
32,6 |
0 |
0 |
0 |
0 |
157,0 |
282,1 |
243,3 |
137,1 |
|
55 |
159,2 |
170,5 |
189,3 |
160,4 |
184,6 |
162,9 |
81,8 |
0 |
0 |
0 |
0 |
0 |
0 |
168,0 |
257,2 |
269,7 |
162,0 |
|
60 |
159,2 |
159,2 |
165,0 |
137,4 |
152,0 |
108,3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
201,9 |
212,9 |
275,0 |
199,0 |
|
65 |
159,2 |
147,1 |
139,5 |
113,2 |
118,2 |
52,6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
185,8 |
161,7 |
247,6 |
230,0 |
|
70 |
159,2 |
134,3 |
112,9 |
88,1 |
83,1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
192,6 |
113,6 |
194,0 |
252,0 |
|
72 |
159,2 |
129,0 |
102,0 |
77,9 |
68,9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
195,0 |
95,9 |
167,0 |
243,2 |
|
74 |
159,2 |
123,6 |
91,0 |
67,5 |
54,6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
197,1 |
79,4 |
139,0 |
225,0 |
|
75 |
159,2 |
121,0 |
85,4 |
62,3 |
47,4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
198,0 |
71,5 |
125,2 |
212,3 |
|
76 |
159,2 |
118,1 |
79,8 |
57,1 |
40,2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
199,0 |
63,8 |
111,1 |
199,0 |
|
78 |
159,2 |
112,6 |
68,6 |
46,6 |
25,7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
199,0 |
49,1 |
84,5 |
165,5 |
|
80 |
159,2 |
106,9 |
57,3 |
36,0 |
11,2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
201,9 |
35,8 |
60,4 |
127,7 |
|
82 |
159,2 |
101,2 |
45,9 |
25,4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
203,0 |
23,8 |
39,5 |
89,1 |
|
84 |
159,2 |
95,4 |
34,5 |
14,7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
203,9 |
13,8 |
22,5 |
53,6 |
|
85 |
159,2 |
92,5 |
28,7 |
9,4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
204,2 |
10,0 |
16,2 |
39,0 |
|
86 |
159,2 |
89,6 |
23,0 |
4,0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
204,5 |
6,2 |
10,1 |
25,0 |
|
88 |
159,2 |
83,6 |
11,5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
204,9 |
1,6 |
2,5 |
6,4 |
|
90 |
159,2 |
77,7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
205,0 |
0 |
0 |
0 |
Типовые кривые силы света светильников, которые могут быть приняты за точечные излучатели могут быть представлены в аналитической форме, учитывая, что значения силы света относятся к источнику света с условным световым потоком Ф = 1000 лм.
для кривой типа «М»
I(a) = 159,2, (1.3.1)
для кривой типа «Д»
I(a) = 330cosa, (1.3.2)
для кривой типа «Д-1»
![]() , (1.3.3)
, (1.3.3)
для кривой типа «Д-2»
![]() , (1.3.4)
, (1.3.4)
для кривой типа «Д-3»
 (1.3.6)
(1.3.6)
для кривой типа «Г»
 (1.3.5)
(1.3.5)
для кривой типа «Г-1»
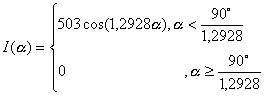 (1.3.7)
(1.3.7)
для кривой типа «Г-2»
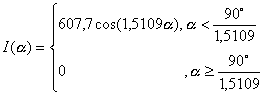 (1.3.8)
(1.3.8)
для кривой типа «Г-3»
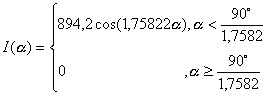 (1.3.9)
(1.3.9)
для кривой типа «К»
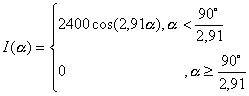 (1.3.10)
(1.3.10)
для кривой типа «К-1»
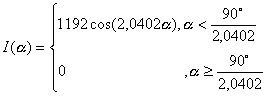 (1.3.11)
(1.3.11)
для кривой типа «К-2»
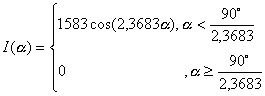 (1.3.12)
(1.3.12)
для кривой типа «К-3»
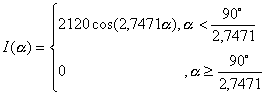 (1.3.13)
(1.3.13)
для кривой типа «С»
I(a) = 205sina, (1.3.14)
для кривой типа «Л»
![]() (1.3.15)
(1.3.15)
для кривой типа «Л-Ш»
![]() (1.3.16)
(1.3.16)
для кривой типа «Ш»
![]() (1.3.17)
(1.3.17)
1.3.2. Для точных вычислений можно аппроксимировать кривую силы света методом наименьших квадратов. Кривая силы света, как любая непрерывная функция может быть представлена полиномом n-ой степени.
![]() (1.3.18)
(1.3.18)
Степень полинома может быть определена из минимума среднеквадратичного отклонения.
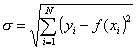 (1.3.19)
(1.3.19)
При низких степенях полинома велики отклонения значений полинома от паспортных значений кривой I(a), что приводит к большому среднеквадратичному отклонению s. При высоких степенях полинома его значения описывают более частные изменения, чем кривая I(a), что так же повышает значение среднеквадратичного отклонения s.
1.3.3. При использовании светильников с несимметричными кривыми сил света, параметры которых задаются 2-мя, 3-мя и более кривыми зависимости I(a) при разных углах b, для определения I(a; b) при углах b, паспортные данные для которых не приводятся, может быть использована интерполяция полиномами Лагранжа, если зависимость I(a; b) от углов b носит линейный характер.
При нелинейном характере зависимости I(a; b) = f(b) следует использовать нелинейные методы интерполяции.
При заданных в паспорте кривых сил света I = I(a) для двух углов b0 и b1 искомые значения можно определить по формуле:
![]() , (1.3.20)
, (1.3.20)
При заданных в паспорте кривых сил света I = I(a) для 3-х углов b: b0, b1, b2 искомые значения I(a; b) можно определить по формуле:
![]() , (1.3.21)
, (1.3.21)
где I1(a), I2(a), I3(a) - значения силы света для искомого угла по паспортным графикам.
При наличии большого числа графических зависимостей I = I(a) для различных значений b в паспорте или каталоге на светильник используются формулы:
![]() , (1.3.22)
, (1.3.22)
![]() (1.2.32)
(1.2.32)
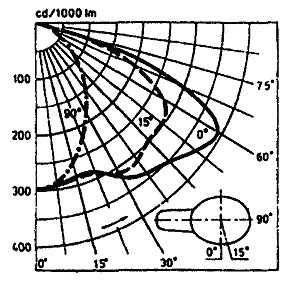
Пример 1. Определить значение условной силы света (Фл = 1000 лм) от светильника с КСС, приведенной на рис. 1.5 в направлении углов a = 30°, b = 45°.
![]()
Паспортное значение I(30°, 45°) = 420 кд. Ошибка в определении I(a; b) составляет 7,1%.
Рис. 1.5. Пример представления КСС несимметричного светильника в каталогах
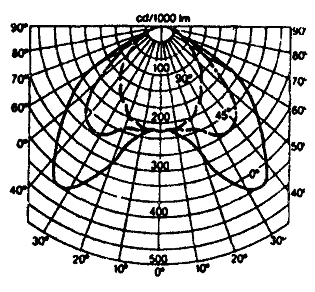
Рис. 1.6. Пример представления КСС несимметричного светильника в каталогах
Пример 2. Определить значение условной силы света (Фл = 1000 лм) от светильника с КСС, приведенной на рис. 1.6. в направлении углов a = 45°, b = 15° (рис. 1.6)
Исходя из паспортных данных на светильник, кривую силы света можно записать
![]()
Паспортное значение I(45°, 15°) = 300 кд. Следовательно, ошибка в определении I составила 10,6%.
1.4. Расчет прямой составляющей освещенности от точечного излучателя
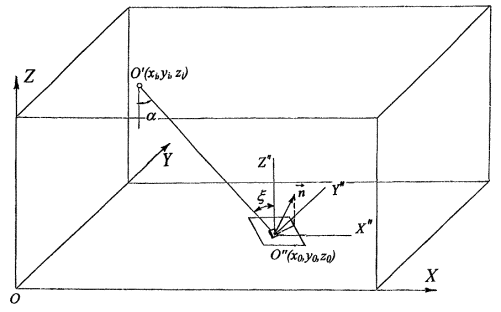
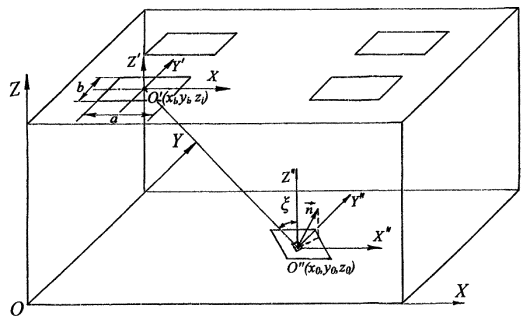
1.4.1. При расчете освещенности и равномерности ее распределения по помещению ориентация расчетной плоскости определяется в сферической системе координат в соответствии с существующими стандартными обозначениями углов полярным q и азимутальным j углами в сферической системе координат O"rqj, центр которой находится в расчетной точке (рис. 1.1). Случай q - q0 относится к горизонтально расположенной плоскости. Случай q = p/2 соответствует пучку вертикальных плоскостей, ориентированных азимутальным углом j .
Положение светильников определяется координатами (xb уb zb) в декартовой системе Oxyz, центр которой помещается в один из углов помещения (рис. 1.7).
Координаты расчетной точки О"(х0, у0, z0) определяются в той же системе координат Oxyz.
Рис. 1.7. Привязка помещения и светильников к осям координат
1.4.2. Расчет прямой составляющей начинается с расчета условной освещенности еn. При этом условно принимается, что суммарный световой поток источников света в светильнике равен 1000 лм. Расчет условной освещенности ведется по формуле:
где Ii(a) - сила света i-го светильника в направлении к точке расчета (тип применяемых светильников в строительном модуле обычно одинаков);
ri - расстояние от i-го светильника до расчетной плоскости;
xi - угол между лучом, падающим в расчетную точку от i-го светильника, и нормалью к расчетной плоскости в данной точке (рис. 1.7);
N - число светильников.
Косинус угла xi и ri определяется по формулам:
![]() . (1.4.3)
. (1.4.3)
где xi, yi, zi - координаты i-го светильника в декартовой системе координат с центром в одном из углов помещения или ячейки (рис. 1.7);
x0, у0, z0 - координаты точки расчета в той же системе.
1.4.3. Значения силы света Ii(a) определяются исходя из паспортных данных светильника (таблицы, графики, формулы), рассчитанных значений угла ai, значения которого определяются из формулы:
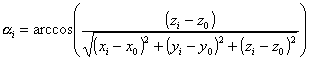 . (1.4.4)
. (1.4.4)
1.4.4. Экранирование светильников расчетной плоскостью учитывается через значение cosxi. При cosxi £ 0 световые лучи от i светильника не падают в расчетную плоскость и ei = 0.
1.4.5. Приведенные формулы (1.4.1) - (1.4.3) обобщают все возможные случаи ориентации расчетной плоскости и удобны для использования при расчете с помощью компьютера.
Частные случаи расположения расчетной плоскости вытекают из формул (1.4.1) - (1.4.3)
Условная освещенность горизонтальной плоскости от i-го светильника рассчитывается по формуле
Условная освещенность вертикальных плоскостей рассчитывается по формуле
![]() . (1.4.6)
. (1.4.6)
Условная освещенность наклонной плоскости только относительно оси Oz (когда j = 00)
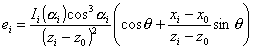 . (1.4.7)
. (1.4.7)
1.4.6. Освещенность в расчетной точке определяется по формуле:
![]() , (1.4.8)
, (1.4.8)
где ![]() - сумма прямой
и отраженной составляющей условной освещенности;
- сумма прямой
и отраженной составляющей условной освещенности;
Ф - суммарный поток источников света в светильнике;
![]() - коэффициент полезного действия светильника
для нижней полусферы.
- коэффициент полезного действия светильника
для нижней полусферы.
1.4.7. Для решения обратной задачи - нахождения светового потока лампы при заданной норме освещенности Ен - расчет светового потока ведется по формуле:
![]() , (1.4.9)
, (1.4.9)
где Ен - норма освещенности;
Кз - коэффициент запаса по действующему СНиП 23-05-96.
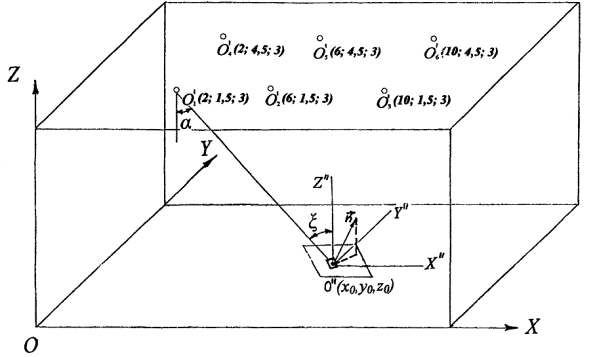
Пример. Помещение размером 12´6´3 м освещается шестью светильниками типа НСП 11-200-231, имеющими кривую силы света типа «Д» и h = 0,67. Источником света служит лампа накаливания Б-215-225-200, имеющая световой поток Фл = 2920 лм. Коэффициенты отражения потолка, стен и пола соответственно равны r = 0,7; 0,5; 0,1. Необходимо определить обеспечивает ли данная осветительная установка нормируемые параметры: освещенность Ен = 75 лк и неравномерность Emax/Emin =1,5.
Светильники располагаются в точках помещения, имеющих координаты: (2; 4,5; 3), (6; 4,5; 3), (10; 4,5; 3), (2; 1,5; 3), (6; 1,5; 3), (10; 1,5; 3) (рис. 1.8).
Исходя из расположения светильников минимальные и максимальные значения освещенности могут быть в следующих контрольных точках, расположенных под светильниками, между светильниками и на пересечении диагоналей: z1 (4; 3; 0,8), z2 (6; 1,5; 0,8), z3 (4; 1,5; 0,8), z4 (1; 3; 0,8), z5 (6; 3; 0,8).
Расчет по формуле (1.4.5) дает следующие значения условной горизонтальной освещенности:
z1 - e1 = 52,84 лк
z2 - e2 = 86,14 лк = emax
z3 - e3 = 51,72 лк
z4 - e4 = 51,53 лк = еmin
z5 - e5 = 74,39 лк
При равномерном освещении с небольшой степенью локализации согласно разделу 1.8 настоящего пособия отраженную составляющую можно считать равномерно распределенной по площади помещения. Индекс помещения равен i = 1,3, для которого hr = 0,33, hч = 0,18. Отсюда отраженная составляющая освещенности равна:
![]()
Минимальное значение прямой составляющей освещенности в помещении равна:
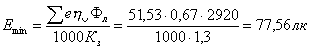
Рис. 1.8. К примеру расчета освещенности.
O - светильник
Неравномерность распределения освещенности будет равна:
![]() .
.
Таким образом, данная осветительная установка удовлетворяет нормам по освещенности, но не удовлетворяет нормам неравномерности распределения освещенности.
1.5. Расчет освещенности от точечного излучателя с несимметричным светораспределением
1.5.1. Методика расчета освещенности для точечного излучателя с несимметричным светораспределением зависит от представления характеристик светораспределения светового прибора и в общем случае идентична методике расчета освещенности, изложенной в разделе 1.4 настоящего пособия.
При известном значении Ii(a,b) расчет условной освещенности следует вести по формуле:
![]() , (1.5.1)
, (1.5.1)
Косинус угла xi и ri определяются по формулам (1.4.2) и (1.4.3), а Ii(a,b) определяется по паспортным данным и интерполяцией.
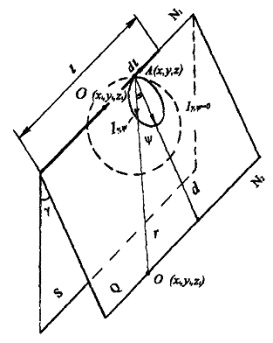
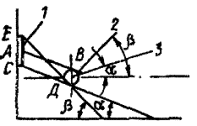
1.5.2. В других случаях кривые силы света некруглосимметричных световых приборов задаются в продольных плоскостях и в поперечных плоскостях в углах g и y (см. рис. 1.9).
Рис. 1.9. К расчету освещенности от точечного источника с несимметричным светораспределением
По углу y они даются в пределах от 0 - 90° при наличии двух плоскостей симметрии, в пределах 0 - 180° при одной плоскости симметрии и 0 - 360° при отсутствии плоскостей симметрии.
Условная освещенность для излучателей данного типа рассчитывается по формуле:
![]() , (1.5.2)
, (1.5.2)
где xi и ri определяются формулами (1.4.2) и (1.4.3). В этом случае угол a между оптической осью излучателя и лучом в расчетную точку может быть представлен в виде (см. рис. 1.9).
cos a = cos g / cos y, (1.5.3)
Если в соответствии с прежними обозначениями xi, yi, zi - координаты i-того светильника, а x0, у0, z0 - координаты расчетной точки А, то:
Тогда для горизонтальной плоскости q = 00, обозначив zi - z0 = h, при i = 1 мы приходим к общеизвестной из литературы формуле расчета освещенности в горизонтальной плоскости от некруглосимметричного излучателя:
![]() . (1.5.6)
. (1.5.6)
Существует несколько распространенных типов кривой силы света некруглосимметричных излучателей.
Первый тип светораспределения подчиняется закону I = I0 в поперечной плоскости и I = I0 cos g в продольной плоскости:
I(g, y) = I0 cos g, (1.5.7)
тогда
![]() . (1.5.8)
. (1.5.8)
Второй тип излучателей обладает светораспределением:
I(g, y) = I0 cos ng cos y, (1.5.9)
тогда
![]() . (1.5.10)
. (1.5.10)
Третий тип излучателей имеет светораспределение вида I = I0 (1 + cos g)/2 в поперечной и I = I0 cos y в продольной плоскости:
![]() , (1.5.11)
, (1.5.11)
тогда
![]() . (1.5.12)
. (1.5.12)
где cos y, cos g, cos x определяются по формулам (1.5.4), (1.5.5) и (1.4.2), а riг по формуле (1.4.3).
1.6. Расчет освещенности от линейных излучателей
1.6.1. За характеристику светораспределения излучателей условно принимают распределение силы света в поперечной плоскости от излучателей единичной длины, обычно I = 1 м. Распределение силы света в поперечной плоскости (перпендикулярной оси источника) может иметь вид: I(g) = I - светораспределение цилиндра; I(g) = I cos g -светораспределение полосы.
В любой продольной плоскости равнояркий линейный излучатель имеет косинусное распределение
I(g, y) = I0 cos g cos y, (1.6.1)
где g - угол в поперечной плоскости (угол между двумя продольными плоскостями, одна из которых соответствует g = 0, а другая проходит через расчетную точку О"(х0, у0, z0); j - угол в продольной плоскости g: между нормалью к оси излучателя и направлением падения светового луча в расчетную точку (рис. 1.10).
Рис. 1.10. К определению углов падения светового потока в расчетную точку
В других случаях светораспределение от линейного излучателя может быть представлено в виде:
I(g, y) = I0 cos g f(y), (1.6.2)
где
f(y) = A cos y + B cos3y + C cos5y. (1.6.3)
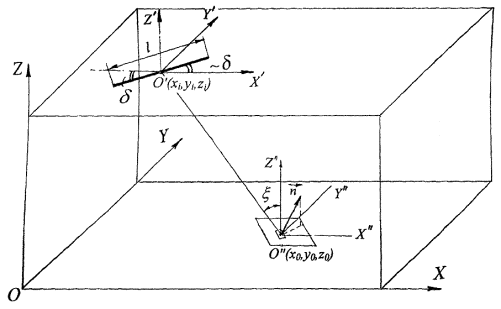
1.6.2. Ориентация расчетной плоскости - Р в пространстве по прежнему задается полярным q и азимутальным j углами в сферической системе координат с центром в расчетной точке О" (x0, y0, z0) (рис. 1.11). Координаты центра линейного O¢ (xi, yi, h) длиной l будем задавать в прямоугольной системе координат OXYZ с центром в одном из углов помещения или строительного модуля.
В общем случае светящаяся линия может быть повернута относительно оси ОХ на угол d (рис. 1.11).
Рис. 1.11. К расчету освещенности от линейного излучателя
1.6.3. Прямая составляющая освещенности при светораспределении I(g) = I0 cos g рассчитывается по формуле:
где m¢ = m cos d + n sin d; n¢ = m sin d - n cos d;
m = xi - x0; n = уi - y0; h0 = zi - z0
Если d = 0, то формула для расчета освещенности принимает вид:
![]() (1.6.7)
(1.6.7)
Значения F1i и F2i рассчитываются по формулам (1.6.5) и (1.6.6) при m¢ = m и n¢ = n.
Выражения (1.6.4) - (1.6.6) описывают освещенность поверхности ориентированной углами q и j в световом поле линейного излучателя, имеющего светораспределения I(g, y) = I0 cos g cos y.
Если светильники располагаются поперек помещения, то d = p/2 в формулах (1.6.5) и (1.6.6) принимаем m¢ = т и n¢ = n, и таким образом, m¢2 и n¢2 меняются местами.
1.6.4. Для горизонтальной плоскости q = q0 и формула для расчета освещенности имеет вид:
Кроме того при m¢ = т = xi - x0 = l/2 как частный случай получаем
общеизвестную формулу справедливую для светораспределения ![]() :
:
При расчете освещенности от реальных светильников делается допущение, что в продольных плоскостях светораспределение является косинусным, а в поперечной плоскости задается паспортной кривой Ig = f(g). В этом случае формула (1.6.9) для расчета освещенности будет иметь вид:
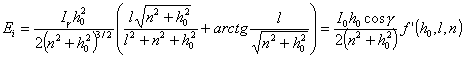 (1.6.10)
(1.6.10)
Пример. Помещение размером 6´3´3,5 м с коэффициентами
отражения потолка, стен и пола 0,7; 0,5; 0,3 освещается светильником с одной
люминесцентной лампой типа ЛБ 58, центр которой располагается в точке (3; 1,5; 3,5).
Необходимо определить освещенность и неравномерность распределения освещенности
в помещении. Источник света ЛБ 58 имеет световой поток Фл = 4800 лм,
длину lл = 1500 мм. Коэффициент полезного действия
светильника в нижнюю полусферу h = ![]() = 70%.
= 70%.
Принимая светильник за светящую линию определим силу света с единицы длины в плоскости перпендикулярной оси лампы:
![]() .
.
Прямая составляющая освещенности в контрольных точках, рассчитанная по формулам (1.6.8) и (1.6.9), равна:
zi (1; 0,75; 0,8) = 18,4 лк = (Еmin)п
z2 (3; 1,5; 0,8) = 50,2 лк = (Еmax)n
Расчет отраженной составляющей освещенности приводится в соответствии с разделом 1.8 настоящего пособия.
В данном случае прямая и отраженная составляющие освещенности распределены с одинаковой степенью неравномерности. Учитывая, что индекс данного помещения i = 0,57, значения коэффициентов использования для указанного помещения согласно справочной литературе hr = 0,28; , hч = 0,16.
Окончательно получаем значения освещенностей:
![]()
![]()
Неравномерность распределения освещенности составит
![]() .
.
1.7. Расчет освещенности от прямоугольных поверхностных излучателей равномерной яркости
1.7.1. Из всевозможных форм и светораспределений поверхностных излучателей в практических случаях наиболее часто встречаются прямоугольные излучатели, яркость которых в первом приближении может считаться равномерной. Это относится к светильникам с люминесцентными лампами, имеющими прямоугольное выходное отверстие, перекрытое светотехническим молочным (рассеивающим) оргстеклом. Светильники такого типа используются для освещения общественных производственных зданий. Поверхностные излучатели треугольной, круглой и более сложных форм используются редко, в основном, в области архитектурного освещения в индивидуальных проектах. В дальнейшем остановимся на решении задачи об определении освещенности произвольно ориентированной плоскости, помещенной в расчетную точку в световом поле равнояркого прямоугольного излучателя.
1.7.2. Ориентация расчетной плоскости в пространстве по прежнему задается полярным q и азимутальным j углами в сферической системе координат с центром в расчетной точке О"rqj (рис. 1.1). Координаты излучателя O¢(xi, yi, zi) будем задавать в прямоугольной системе координат OXYZ, расположенной в одном из углов помещения или строительного модуля, как это показано на рис. 1.12. При этом высоту подвеса излучателя считаем неизменной zi = h.
Рис. 1.12. К расчету освещенности от прямоугольного излучателя
1.73. Освещенность в точке О"(х0, у0, z0) в плоскости Р определяется по формуле:
Коэффициенты F1i, F2i, F3i определяются по формулам:
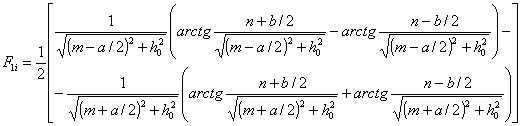 , (1.7.2)
, (1.7.2)
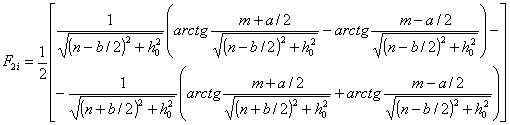 , (1.7.3)
, (1.7.3)
где m = xi - x0; n = yi - y0; h0 = zi - z0
Если прямоугольный излучатель повернут на угол a относительно оси Ох , то в формулах (1.7.1) - (1.7.4):
m = (xi - x0) cos a + (yi - y0) sin a;
n = -(xi - x0) sin a + (yi - y0) cos a
Формулы (1.7.1) - (1.7.4) позволяют рассчитывать освещенность в плоскости, ориентированной полярным q и азимутальными j углами, в световом поле равнояркого прямоугольного излучателя.
Все остальные формулы для расчета освещенности вытекают как частные случаи из выражений (1.7.1) - (1.7.4). Так в случае расчета освещенности от светящего прямоугольника плоскость которого параллельна расчетной плоскости: т = а/2; п = b/2; q = 0 и получается формула Ратнера:
 . (1.7.5)
. (1.7.5)
При q = p/2; j = 0; т = а/2; п = b/2 имеет случай светящего прямоугольника, плоскость которого перпендикулярна расчетной плоскости, и получаем другую формулу Ратнера.
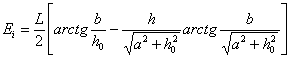 . (1.7.6)
. (1.7.6)
Пример. Помещение 6´4´3 м освещается светильниками типа ВЛВ 4´40, имеющими размер а = 1,2 м и в = 0,5 м и среднюю габаритную яркость L = 6000 кд/м2. Геометрические центры светильников расположены в точках (1,5; 1; 3), (4,5; 1; 3), (1,5; 3; 3), (4,5; 3; 3). Определить прямую составляющую, освещенности и неравномерность распределения освещения по помещению на уровне условной рабочей поверхности (0,8 м от пола).
Освещенность в контрольных точках равна:
![]()
- в точке 1 с координатами (3; 2; 0,8) - E1 = 452 лк
- в точке 2 с координатами (1,5; 1; 0,8) - Е2 = 474 лк
- в точке 3 с координатами (1; 2; 0,8) - Е3 = 432 лк
Неравномерность распределения освещенности будет равна:
![]()
1.8. Учет отраженной составляющей освещенности
1.8.1. При высоких коэффициентах отражения потолка, стен, пола, а также в тех случаях, когда светильники не относятся к классу прямого света, при точечном методе расчета необходимо учитывать отраженную составляющую освещенности. В данном случае удобно воспользоваться известными приближенными решениями.
1.8.2. При равномерном освещении или при небольшой степени локализации отраженную составляющую можно считать равномерно распределенной по площади помещения, равной:
где hr - коэффициент использования при заданных значениях коэффициентов отражения потолка, стен, расчетной поверхности или пола rп, rс, rр.
hч - коэффициент использования черного помещения rп = rс = rр = 0.
Ф - световой поток источника света с учетом к.п.д. светильника.
При расчете осветительной установки на нормируемую освещенность с учетом отраженной составляющей в формулу (1.8.1) вводится коэффициент запаса:
![]() . (1.8.2)
. (1.8.2)
1.8.3. В случае сильно выраженной
локализации освещения допустимо считать, что прямая и отраженная составляющие
освещенности распределены с одинаковой степенью неравномерности. В этом случае
суммарная освещенность умножается на коэффициент ![]() :
:
![]() . (1.8.3)
. (1.8.3)
1.9. Расчет осветительных установок методом коэффициента использования
1.9.1. Коэффициент использования Uoy определяется как отношение светового потока, падающего на расчетную плоскость, к световому потоку источников света. Он зависит от светораспределения светильников и их размещения в помещении; от размеров освещаемого помещения и отражающих свойств его поверхностей; от отражающих свойств рабочей поверхности.
Требуемый световой поток ламп в каждом светильнике находится по формуле:
где Ен - нормируемое значение освещенности; Кз - коэффициент запаса по СНиП 23-05-95; S - освещаемая площадь; z = Eср/Емин; Eср, Емин - среднее и минимальное значения освещенности; п - число светильников; Uoy - коэффициент использования светового потока.
Входящий в формулу (1.9.1) коэффициент z характеризует неравномерность освещения. В наибольшей степени z зависит от отношения расстояния между светильниками к расчетной высоте (L/hp). При L/hp, не превышающем рекомендуемых значений (L £ hp), принимается z = 1,15 для ЛН и ДРЛ и z = 1,10 для люминесцентных ламп при расположении светильников в виде светящихся линий. Для отраженного освещения принимается z = 1,0; при расчете на среднюю освещенность z не учитывается.
1.9.2. Соотношение размеров освещаемого помещения и высота подвеса светильников в нем характеризуются индексом помещения.
![]() , (1.9.2)
, (1.9.2)
где А - длина помещения; В - его ширина; hp - расчетная высота подвеса светильников.
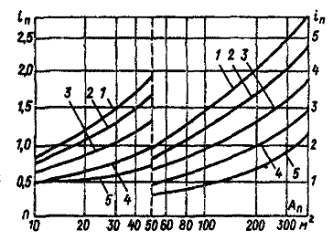
Упрощенно индекс помещений может быть определен с помощью табл. 1.9.1 и 1.9.2).
Индекс помещения in находится по известной площади помещения S и высоте подвеса светильника hp по табл. 1.9.1 при А/В £ 3. Для удлиненных помещений (когда А/В > 3), in определяется по табл. 1.9.2.
Таблица 1.9.1
ИНДЕКС ПОМЕЩЕНИЯ in ПРИ А/В £ 3
|
Площадь помещения S, м2 |
Значение in при расчетной высоте hр, м равной |
||||||||||||||
|
2,0 |
2,2 |
2,5 |
2,7 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
7,0 |
8,0 |
9,0 |
10,0 |
|
|
10 |
0,8 |
0,7 |
0,6 |
0,6 |
0,5 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
15 |
0,9 |
0,8 |
0,76 |
0,76 |
0,5 |
0,5 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
17 |
1,0 |
0,9 |
0,8 |
0,7 |
0,7 |
0,6 |
0,5 |
- |
- |
- |
- |
- |
- |
- |
- |
|
20 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,5 |
- |
- |
- |
- |
- |
- |
- |
|
25 |
1,2 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,5 |
- |
- |
- |
- |
- |
- |
|
30 |
1,2 |
1,2 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,5 |
- |
- |
- |
- |
- |
|
40 |
1,5 |
1,5 |
1,2 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,6 |
0,5 |
- |
- |
- |
- |
|
50 |
1,7 |
1,5 |
1,2 |
1,2 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,6 |
0,5 |
- |
- |
- |
|
60 |
1,7 |
1,7 |
1,5 |
1,5 |
1,2 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
- |
- |
- |
|
70 |
2,0 |
1,7 |
1,5 |
1,5 |
1,2 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,7 |
0,6 |
0,5 |
- |
- |
|
80 |
2,25 |
2,0 |
1,7 |
1,5 |
1,5 |
1,2 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
- |
- |
|
90 |
2,2 |
2,0 |
1,7 |
1,5 |
1,5 |
1,2 |
1,1 |
1,0 |
0,9 |
0,8 |
0,8 |
0,7 |
0,6 |
0,5 |
- |
|
100 |
2,5 |
2,2 |
2,0 |
1,7 |
1,5 |
1,5 |
1,2 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
- |
|
120 |
2,5 |
2,2 |
2,0 |
2,0 |
1,7 |
1,5 |
1,2 |
1,1 |
1,0 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
|
150 |
3,0 |
2,5 |
2,2 |
2,2 |
2,0 |
1,7 |
1,5 |
1,2 |
1,1 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
0,6 |
|
200 |
3,5 |
3,0 |
2,5 |
2,5 |
2,2 |
2,0 |
1,7 |
1,5 |
1,25 |
1,25 |
1,1 |
1,0 |
0,9 |
0,8 |
0,7 |
|
250 |
4,0 |
3,5 |
3,0 |
3,0 |
2,5 |
2,2 |
2,0 |
1,7 |
1,5 |
1,5 |
1,25 |
1,1 |
1,0 |
0,9 |
0,8 |
|
300 |
4,0 |
4,0 |
3,5 |
3,0 |
2,5 |
2,2 |
2,0 |
1,7 |
1,75 |
1,5 |
1,25 |
1,1 |
1,0 |
0,9 |
0,8 |
|
350 |
4,0 |
4,0 |
3,5 |
3,5 |
3,0 |
2,5 |
2,2 |
2,0 |
1,75 |
1,75 |
1,5 |
1,25 |
1,1 |
1,0 |
0,9 |
|
400 |
5,0 |
4,0 |
4,09 |
3,5 |
3,0 |
2,5 |
2,5 |
2,25 |
2,0 |
1,75 |
1,5 |
1,25 |
1,25 |
1,1 |
1,0 |
|
450 |
5,0 |
5,0 |
4,0 |
4,0 |
3,5 |
3,0 |
2,5 |
2,2 |
2,0 |
1,75 |
1,75 |
1,5 |
1,25 |
1,1 |
1,0 |
|
500 |
- |
5,0 |
4,0 |
4,0 |
3,5 |
3,0 |
2,5 |
2,5 |
2,0 |
2,0 |
1,75 |
1,5 |
1,25 |
1,2 |
1,1 |
|
600 |
- |
- |
5,0 |
4,0 |
4,0 |
3,5 |
3,0 |
2,5 |
2,25 |
2,0 |
2,0 |
1,75 |
1,5 |
1,2 |
1,1 |
|
700 |
- |
- |
5,0 |
5,0 |
4,0 |
3,5 |
3,0 |
3,0 |
2,50 |
2,25 |
2,0 |
1,75 |
1,5 |
1,5 |
1,25 |
|
800 |
- |
- |
- |
5,0 |
5,0 |
4,0 |
3,5 |
3,0 |
2,50 |
2,50 |
2,25 |
2,0 |
1,75 |
1,5 |
1,25 |
|
900 |
- |
- |
- |
- |
5,0 |
4,0 |
3,5 |
3,0 |
3,0 |
2,5 |
2,25 |
2,0 |
1,75 |
1,5 |
1,5 |
|
1000 |
- |
- |
- |
- |
5,0 |
4,0 |
4,0 |
3,5 |
3,0 |
3,0 |
2,5 |
2,25 |
2,0 |
1,7 |
1,5 |
|
1200 |
- |
- |
- |
- |
- |
5,0 |
4,0 |
3,5 |
3,5 |
3,0 |
2,5 |
2,25 |
2,0 |
1,7 |
1,75 |
|
1400 |
- |
- |
- |
- |
- |
5,0 |
4,0 |
4,0 |
3,5 |
3,5 |
3,0 |
2,5 |
2,25 |
2,0 |
1,75 |
|
1600 |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
4,0 |
3,5 |
3,0 |
2,5 |
2,5 |
2,0 |
2,0 |
|
1800 |
- |
- |
- |
- |
- |
- |
5,0 |
5,0 |
4,0 |
3,5 |
3,5 |
3,0 |
2,5 |
2,2 |
2,0 |
|
2000 |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
4,0 |
3,5 |
3,0 |
2,5 |
2,5 |
2,25 |
|
2500 |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
4,0 |
3,5 |
3,0 |
2,5 |
2,5 |
|
3000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
4,0 |
3,5 |
3,0 |
2,5 |
|
3500 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
5,0 |
4,0 |
3,5 |
3,0 |
3,0 |
|
4000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
4,0 |
3,5 |
3,0 |
|
4500 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
3,5 |
3,0 |
|
5000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
4,0 |
3,5 |
|
6000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
3,5 |
|
7000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
4,0 |
|
8000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
|
9000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
4,0 |
|
10000 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
5,0 |
1.9.3. Коэффициенты отражения поверхностей помещения: потолка rп и стен rс - можно приближенно оценить по табл. 1.9.3. Коэффициент отражения расчетной поверхности или пола как правило принимается rр = 0,1.
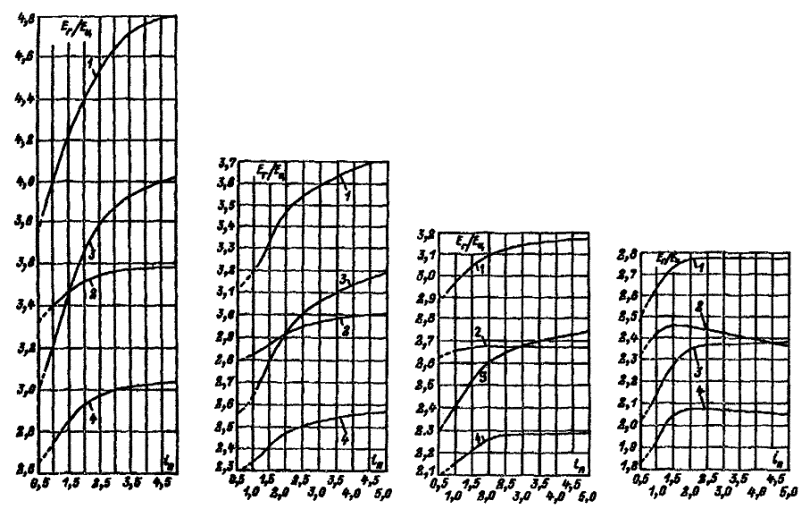
1.9.4. Коэффициент использования Uоу определяется по найденным значениям индекса помещения in и коэффициентов отражения rп, rс и rр для выбранного типа светильников. Значения коэффициентов использования для светильников с типовыми кривыми силами света приведены в табл. 1.9.4.
В тех случаях, когда в таблицах отсутствуют данные о коэффициенте использования светильников, например, новых модификаций, эти коэффициенты приближенно могут быть определены следующим путем: по форме кривой силы света в нижней полусфере определяется ее тип, по каталожным данным светильника определяются (в процентах потока лампы) потоки нижней Ф◡ и верхней Ф◠ полусфер; первый умножается на коэффициент использования по таблице 1.9.5, второй - по таблице 1.9.6. Сумма произведений дает общий полезный поток, делением которого на поток лампы (обычно 1000 лм) находится коэффициент использования.
Таблица 1.9.2
ИНДЕКС ПОМЕЩЕНИЯ in, ПРИ A/В > 3
|
Значение in при расчетной высоте hp, м. |
|||||||||||||||||
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,25 |
1,5 |
1,75 |
2,0 |
2,25 |
2,5 |
3,0 |
3,5 |
4,0 |
5,0 |
|
|
3 - 4 |
- |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,25 |
1,5 |
1,75 |
2,0 |
2,25 |
2,5 |
3,0 |
3,5 |
4,0 |
|
5 - 6 |
- |
0,5 |
0,5 |
0,6 |
0,7 |
0,8 |
0,8 |
0,9 |
1,1 |
1,25 |
1,5 |
1,75 |
2,0 |
2,25 |
2,5 |
3,0 |
4,0 |
|
7 - 9 |
- |
- |
0,5 |
0,5 |
0,6 |
0,7 |
0,7 |
0,8 |
1,0 |
1,1 |
1,25 |
1,5 |
1,75 |
2,0 |
2,25 |
2,5 |
3,5 |
|
10 |
- |
- |
- |
0,5 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,1 |
1,25 |
1,25 |
1,5 |
1,75 |
2,0 |
2,5 |
3,0 |
|
15 |
- |
- |
- |
- |
0,5 |
0,5 |
0,6 |
0,6 |
0,8 |
0,1 |
1,0 |
1,1 |
1,95 |
1,5 |
1,75 |
90 |
2,5 |
|
20 |
- |
- |
- |
- |
- |
- |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,25 |
1,5 |
1,75 |
2,25 |
|
30 |
- |
- |
- |
- |
- |
- |
- |
0,5 |
0,6 |
0,6 |
0,7 |
0,8 |
0,9 |
1,1 |
1,25 |
1,5 |
1,75 |
|
40 - 50 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,1 |
1,25 |
1,5 |
Таблица 1.9.3
ПРИБЛИЗИТЕЛЬНЫЕ ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ ОТРАЖЕНИЯ СТЕН И ПОТОЛКА
|
Коэффициент отражения, % |
|
|
Побеленный потолок; побеленные стены с окнами, закрытыми белыми шторами |
70 |
|
Побеленные стены при незанавешенных окнах; побеленный потолок в сырых помещениях; чистый бетонный и светлый деревянный потолок |
50 |
|
Бетонный потолок в грязных помещениях; деревянный потолок; бетонные стены с окнами; стены, оклеенные светлыми обоями |
30 |
|
Стены и потолки в помещениях с большим количеством темной пыли; сплошное остекление без штор; красный кирпич неоштукатуренный; стены с темными обоями |
10 |
Таблица 1.9.4
КОЭФФИЦИЕНТ ИСПОЛЬЗОВАНИЯ СВЕТИЛЬНИКОВ С ТИПОВЫМ КРИВЫМИ СИЛАМИ СВЕТА Uoy
|
Значение Uоу, % |
||||||||||||||||||||||||
|
при rп = 0,7; rс = 0,5; rр = 0,3 и in, равном |
при rп = 0,7; rс = 0,5; rр = 0,1 и in, равном |
при rп = 0,7; rс = 0,3; rр = 0,1 и in, равном |
при rп = rс = 0,5; rр = 0,3 и in, равном |
|||||||||||||||||||||
|
0,6 |
0,8 |
1,25 |
2 |
3 |
5 |
0,6 |
0,8 |
1,25 |
2 |
3 |
5 |
0,6 |
0,8 |
1,25 |
2 |
3 |
5 |
0,6 |
0,8 |
1,25 |
2 |
3 |
5 |
|
|
М |
35 |
50 |
61 |
73 |
83 |
95 |
34 |
47 |
56 |
66 |
75 |
86 |
26 |
36 |
46 |
56 |
67 |
80 |
32 |
45 |
55 |
67 |
74 |
84 |
|
Д-1 |
36 |
50 |
58 |
72 |
81 |
90 |
36 |
47 |
56 |
63 |
73 |
79 |
28 |
40 |
49 |
59 |
68 |
74 |
36 |
48 |
57 |
66 |
76 |
85 |
|
Д-2 |
44 |
52 |
68 |
84 |
93 |
103 |
42 |
51 |
64 |
75 |
84 |
92 |
33 |
43 |
56 |
74 |
80 |
76 |
42 |
51 |
65 |
71 |
90 |
85 |
|
Г-1 |
49 |
60 |
75 |
90 |
101 |
106 |
48 |
57 |
71 |
82 |
89 |
94 |
42 |
52 |
69 |
78 |
73 |
76 |
45 |
56 |
65 |
78 |
76 |
84 |
|
Г-2 |
58 |
68 |
82 |
96 |
102 |
109 |
55 |
64 |
78 |
86 |
92 |
96 |
48 |
60 |
73 |
84 |
90 |
94 |
55 |
66 |
80 |
92 |
96 |
103 |
|
Г-3 |
64 |
74 |
85 |
95 |
100 |
105 |
62 |
70 |
79 |
80 |
90 |
93 |
57 |
66 |
76 |
84 |
84 |
91 |
63 |
72 |
83 |
91 |
96 |
100 |
|
К-1 |
74 |
83 |
90 |
96 |
100 |
106 |
69 |
76 |
83 |
88 |
91 |
92 |
65 |
73 |
81 |
86 |
89 |
90 |
70 |
78 |
86 |
92 |
96 |
100 |
|
К-2 |
75 |
84 |
95 |
104 |
108 |
115 |
71 |
78 |
87 |
95 |
97 |
100 |
67 |
75 |
84 |
93 |
97 |
100 |
72 |
80 |
91 |
99 |
103 |
108 |
|
К-3 |
76 |
85 |
96 |
106 |
110 |
116 |
73 |
80 |
90 |
94 |
99 |
102 |
68 |
77 |
86 |
95 |
98 |
101 |
74 |
83 |
93 |
101 |
106 |
170 |
Продолжение таблицы 1.9.4
|
Тип КСС |
Значение Uоу, % |
||||||||||||||||||||||||
|
при rп = rс = 0,5; rр = 0,3 и in, равном |
при rп = 0,5; rс = 0,3; rр = 0,1 и in, равном |
при rп = 0,3; rс = rр = 0,1 и in, равном |
при rп = rс = rр = 0 и in, равном |
||||||||||||||||||||||
|
0,6 |
0,8 |
1,25 |
2 |
3 |
5 |
0,6 |
0,8 |
1,25 |
2 |
3 |
5 |
0,6 |
0,8 |
1,25 |
2 |
3 |
5 |
0,6 |
0,8 |
1,25 |
2 |
3 |
5 |
||
|
Л |
32 |
49 |
59 |
71 |
83 |
91 |
31 |
46 |
55 |
65 |
74 |
83 |
24 |
40 |
50 |
62 |
71 |
77 |
32 |
47 |
57 |
69 |
79 |
90 |
|
|
М |
31 |
43 |
53 |
63 |
72 |
80 |
23 |
36 |
45 |
56 |
65 |
75 |
17 |
29 |
38 |
46 |
58 |
67 |
16 |
28 |
38 |
45 |
55 |
65 |
|
|
Д-1 |
34 |
47 |
54 |
63 |
70 |
77 |
27 |
40 |
48 |
55 |
65 |
73 |
27 |
35 |
42 |
52 |
61 |
68 |
21 |
33 |
40 |
49 |
58 |
66 |
|
|
Д-2 |
40 |
48 |
61 |
74 |
82 |
84 |
33 |
42 |
52 |
69 |
75 |
86 |
28 |
36 |
48 |
63 |
75 |
81 |
25 |
33 |
47 |
61 |
70 |
78 |
|
|
Г-1 |
44 |
53 |
69 |
77 |
83 |
80 |
41 |
48 |
64 |
76 |
70 |
88 |
35 |
45 |
60 |
73 |
68 |
77 |
34 |
44 |
56 |
71 |
68 |
74 |
|
|
Г-2 |
53 |
63 |
76 |
85 |
90 |
94 |
48 |
58 |
72 |
83 |
86 |
93 |
43 |
54 |
68 |
79 |
85 |
90 |
43 |
53 |
66 |
77 |
82 |
86 |
|
|
Г-3 |
61 |
68 |
78 |
84 |
88 |
91 |
57 |
65 |
75 |
83 |
86 |
90 |
53 |
62 |
73 |
80 |
84 |
86 |
53 |
61 |
71 |
78 |
82 |
85 |
|
|
К-1 |
68 |
77 |
83 |
86 |
89 |
90 |
64 |
73 |
80 |
86 |
88 |
90 |
62 |
71 |
77 |
83 |
86 |
88 |
60 |
69 |
77 |
84 |
85 |
86 |
|
|
К-2 |
71 |
78 |
87 |
93 |
98 |
99 |
68 |
74 |
84 |
92 |
93 |
99 |
68 |
72 |
80 |
89 |
93 |
97 |
65 |
71 |
79 |
88 |
92 |
95 |
|
|
К-3 |
72 |
79 |
88 |
94 |
97 |
99 |
68 |
76 |
85 |
93 |
95 |
99 |
64 |
73 |
83 |
90 |
94 |
97 |
64 |
72 |
81 |
88 |
91 |
94 |
|
|
Л |
30 |
45 |
55 |
65 |
70 |
78 |
24 |
40 |
49 |
60 |
70 |
76 |
20 |
35 |
44 |
48 |
65 |
69 |
17 |
33 |
42 |
53 |
63 |
70 |
|
|
Л-Ш |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
12 |
26 |
35 |
47 |
58 |
68 |
|
|
Ш |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
9 |
17 |
25 |
36 |
49 |
62 |
|
1.9.5. Расчет средней освещенности помещения методом коэффициента использования проводится в следующей последовательности:
- определяется hp, тип и число светильников п в помещении, как указывалось выше;
- по таблицам СНиП 23-05-95 находятся коэффициент запаса Кз; поправочный коэффициент z; нормированную освещенность Ен определяют по МГСН 2.06-99; определяется индекс помещения in по таблицам 1.9.1 и 1.9.2;
- определяется коэффициент использования светового потока ламп Uоу;
- по формуле (1.9.1) находится необходимый световой поток ламп в одном светильнике;
- выбирается лампа с близким по величине световым потоком.
Таблица 1.9.5
КОЭФФИЦИЕНТ ИСПОЛЬЗОВАНИЯ СВЕТОВОГО ПОТОКА СВЕТИЛЬНИКОВ С ТИПОВЫМИ КРИВЫМИ СИЛЫ СВЕТА, ИЗЛУЧАЕМОГО В НИЖНЮЮ ПОЛУСФЕРУ
|
Равномерная М |
Конусная Л |
Глубокая Г |
||||||||||||||||||||||
|
rп % |
70 |
50 |
30 |
0 |
70 |
50 |
30 |
0 |
70 |
50 |
30 |
0 |
||||||||||||
|
rс % |
50 |
30 |
50 |
30 |
10 |
0 |
50 |
30 |
50 |
30 |
10 |
0 |
50 |
30 |
50 |
30 |
10 |
0 |
||||||
|
rр % |
30 |
10 |
30 |
10 |
10 |
10 |
0 |
30 |
10 |
30 |
10 |
К |
> 1 |
10 |
0 |
30 |
10 |
30 |
10 |
10 |
10 |
0 |
||
|
Значение in: |
Коэффициент использования, % |
|||||||||||||||||||||||
|
0,5 |
28 |
28 |
21 |
21 |
25 |
19 |
15 |
13 |
36 |
35 |
30 |
30 |
34 |
28 |
25 |
22 |
58 |
57 |
55 |
53 |
57 |
53 |
49 |
47 |
|
0,6 |
35 |
34 |
27 |
26 |
31 |
24 |
18 |
17 |
43 |
42 |
35 |
34 |
40 |
33 |
28 |
27 |
68 |
65 |
62 |
60 |
64 |
60 |
57 |
56 |
|
0,7 |
44 |
39 |
32 |
31 |
39 |
31 |
25 |
24 |
48 |
47 |
41 |
38 |
45 |
38 |
33 |
31 |
74 |
69 |
68 |
64 |
69 |
64 |
61 |
61 |
|
0,8 |
49 |
46 |
38 |
36 |
43 |
36 |
29 |
28 |
54 |
51 |
45 |
43 |
49 |
43 |
37 |
36 |
78 |
73 |
72 |
69 |
72 |
69 |
66 |
64 |
|
0,9 |
51 |
48 |
40 |
39 |
46 |
39 |
31 |
30 |
57 |
55 |
48 |
46 |
52 |
46 |
41 |
39 |
81 |
76 |
75 |
72 |
75 |
72 |
70 |
67 |
|
1,0 |
54 |
50 |
43 |
41 |
48 |
41 |
34 |
32 |
60 |
57 |
52 |
50 |
55 |
49 |
45 |
42 |
84 |
78 |
78 |
75 |
77 |
74 |
72 |
70 |
|
1,1 |
56 |
52 |
46 |
43 |
50 |
43 |
35 |
33 |
64 |
60 |
55 |
52 |
58 |
51 |
47 |
44 |
87 |
81 |
80 |
77 |
79 |
76 |
74 |
72 |
|
1,25 |
59 |
55 |
49 |
46 |
53 |
45 |
38 |
35 |
69 |
63 |
60 |
56 |
61 |
55 |
50 |
48 |
90 |
83 |
84 |
79 |
82 |
79 |
76 |
75 |
|
1,50 |
64 |
59 |
53 |
50 |
56 |
49 |
42 |
39 |
75 |
69 |
67 |
62 |
67 |
61 |
55 |
53 |
94 |
86 |
88 |
83 |
85 |
82 |
79 |
78 |
|
1,75 |
68 |
62 |
57 |
53 |
60 |
53 |
45 |
42 |
79 |
72 |
71 |
66 |
70 |
65 |
60 |
57 |
97 |
88 |
92 |
85 |
86 |
85 |
82 |
80 |
|
2,0 |
73 |
65 |
61 |
56 |
63 |
56 |
48 |
45 |
83 |
75 |
75 |
69 |
73 |
68 |
64 |
61 |
99 |
90 |
95 |
88 |
88 |
87 |
84 |
82 |
|
2,25 |
76 |
68 |
65 |
60 |
66 |
59 |
51 |
48 |
86 |
77 |
79 |
73 |
76 |
71 |
66 |
64 |
101 |
92 |
97 |
90 |
90 |
88 |
85 |
83 |
|
2,5 |
79 |
70 |
68 |
63 |
68 |
61 |
54 |
51 |
89 |
80 |
82 |
75 |
78 |
73 |
69 |
66 |
103 |
93 |
99 |
91 |
91 |
89 |
87 |
85 |
|
3,0 |
83 |
75 |
73 |
67 |
72 |
65 |
58 |
55 |
93 |
83 |
86 |
79 |
81 |
77 |
73 |
71 |
105 |
94 |
102 |
92 |
93 |
91 |
89 |
86 |
|
3,5 |
87 |
78 |
77 |
70 |
75 |
68 |
61 |
59 |
96 |
86 |
90 |
82 |
83 |
80 |
76 |
73 |
107 |
95 |
104 |
94 |
94 |
93 |
90 |
88 |
|
4,0 |
91 |
80 |
81 |
73 |
78 |
72 |
65 |
62 |
99 |
88 |
93 |
84 |
85 |
83 |
79 |
76 |
109 |
96 |
105 |
94 |
94 |
94 |
91 |
89 |
|
5,0 |
95 |
83 |
86 |
77 |
80 |
75 |
69 |
65 |
105 |
90 |
98 |
88 |
88 |
85 |
81 |
79 |
111 |
97 |
108 |
96 |
96 |
95 |
92 |
90 |
Таблица 1.9.6
КОЭФФИЦИЕНТ ИСПОЛЬЗОВАНИЯ СВЕТОВОГО ПОТОКА СВЕТИЛЬНИКОВ (ЛЮБОГО ТИПА), ИЗЛУЧАЕМОГО В ВЕРХНЮЮ ПОЛУСФЕРУ
|
Потолочные |
Подвесные |
||||||||||||||
|
rп % |
70 |
50 |
30 |
70 |
50 |
30 |
|||||||||
|
rс % |
50 |
30 |
50 |
30 |
10 |
50 |
30 |
50 |
30 |
10 |
|||||
|
rр % |
30 |
10 |
30 |
10 |
10 |
10 |
30 |
10 |
30 |
10 |
10 |
10 |
|||
|
Значение in: |
Коэффициент использования, % |
||||||||||||||
|
0,5 |
26 |
25 |
20 |
19 |
17 |
13 |
6 |
19 |
18 |
15 |
14 |
11 |
9 |
4 |
|
|
0,6 |
30 |
28 |
24 |
23 |
20 |
16 |
8 |
21 |
22 |
18 |
18 |
14 |
11 |
5 |
|
|
0,7 |
34 |
32 |
28 |
27 |
22 |
19 |
10 |
27 |
26 |
22 |
21 |
16 |
13 |
6 |
|
|
0,8 |
38 |
36 |
31 |
30 |
24 |
21 |
11 |
31 |
29 |
25 |
25 |
18 |
16 |
7 |
|
|
0,9 |
40 |
38 |
34 |
33 |
26 |
23 |
12 |
34 |
32 |
28 |
28 |
20 |
18 |
8 |
|
|
1,0 |
43 |
41 |
37 |
35 |
28 |
25 |
13 |
37 |
35 |
32 |
30 |
22 |
20 |
9 |
|
|
1,1 |
46 |
43 |
39 |
37 |
30 |
26 |
14 |
40 |
37 |
34 |
33 |
24 |
21 |
11 |
|
|
1,25 |
49 |
46 |
42 |
40 |
32 |
28 |
15 |
43 |
41 |
38 |
36 |
26 |
24 |
12 |
|
|
1,5 |
54 |
49 |
47 |
44 |
34 |
31 |
17 |
48 |
44 |
42 |
40 |
29 |
26 |
14 |
|
|
1,75 |
57 |
52 |
51 |
47 |
36 |
33 |
18 |
52 |
48 |
46 |
43 |
31 |
29 |
15 |
|
|
2,0 |
60 |
54 |
54 |
50 |
38 |
35 |
19 |
55 |
50 |
50 |
46 |
33 |
31 |
16 |
|
|
2,25 |
62 |
56 |
57 |
52 |
39 |
37 |
20 |
58 |
52 |
53 |
49 |
35 |
33 |
17 |
|
|
2,5 |
64 |
58 |
59 |
54 |
40 |
38 |
21 |
60 |
54 |
55 |
51 |
36 |
34 |
18 |
|
|
3,0 |
68 |
60 |
63 |
57 |
42 |
40 |
22 |
64 |
57 |
59 |
54 |
39 |
36 |
20 |
|
|
3,5 |
70 |
62 |
66 |
59 |
43 |
41 |
23 |
67 |
60 |
62 |
56 |
40 |
39 |
21 |
|
|
4,0 |
72 |
64 |
68 |
61 |
45 |
42 |
24 |
69 |
61 |
65 |
58 |
42 |
40 |
22 |
|
|
5,0 |
75 |
66 |
72 |
64 |
46 |
44 |
25 |
73 |
64 |
69 |
62 |
44 |
42 |
24 |
|
1.9.6. Световой поток светильника при выбранных лампах не должен отличаться от Фл больше чем на величину (-10 ¸ +20)%. В случае невозможности выбора ламп с таким приближением корректируется число светильников п либо высота подвеса светильников hp.
1.9.7. Расчет люминесцентного освещения начинается с выбора числа рядов светильников N, которые подставляются в формулу (1.9.1) вместо п. Первоначально определяется световой поток Фл от ряда светильников. Число светильников в ряду определяется как:
n = Фл/Ф1, (1.9.3)
где Ф1 - световой поток одного светильника.
Суммарная длина n светильников сопоставляется с длиной помещения, причем возможны следующие случаи:
1. Суммарная длина светильников превышает длину помещения: необходимо или применить более мощные лампы (у которых световой поток на единицу длины больше), или увеличить число рядов, или компоновать ряды из сдвоенных, строенных светильников.
2. Суммарная длина светильников равна длине помещения: задача решается установкой непрерывного ряда светильников.
3. Суммарная длина светильников меньше длины помещения: принимается ряд с равномерно распределенными вдоль него разрывами l между светильниками.
Из нескольких возможных вариантов на основе технико-экономических соображений выбирается наилучший.
Рекомендуется, чтобы l не превышала 0,5 расчетной высоты (кроме многоламповых светильников в помещениях общественных и административных зданий).
При заданном световом потоке ряда светильников Фл формула (1.9.1) решается относительно N.
Пример. В помещении габаритами 20 ´ 10 м, с индексом in = 1,25 установлены три продольных ряда светильников ЛСП02 (КСС типа Д-2) с лампами ЛБ и требуется обеспечить Е = 300 лк при К = 1,5. Задано rп = 50 %, rс = 30 %, rр = 10 % и z = 1,15. В табл. 1.9.4 этим условиям соответствует Uoy = 0,52. Световой поток ламп одного ряда светильников:
![]()
Если применить светильники с лампами 2 ´ 40 Вт (с общим световым потоком 6300 лм), то в ряду необходимо установить 63460 : 6300 » 11 светильников; если же светильники с лампами 2 ´ 65 Вт (с потоком 9600 лм), в ряду необходимы 6 светильников. Так как длина помещения не менее 20 м, то в обоих случаях светильники вмещаются в ряд. Некоторые преимущества имеет первый вариант, при котором разрывы между светильниками меньше.
1.10. Расчет освещенности методом удельной мощности
1.10.1. Удельная мощность осветительной установки определяется как частное от деления общей мощности установленных в помещении ламп на площадь помещения (Вт/м2).
где Рл - мощность одной лампы, Вт; п - число ламп; S - площадь помещенья, м2.
Формула (1.10.1) может быть получена путем преобразования формулы (1.9.1), если ввести в нее следующие величины: W - удельную мощность, Вт/м2; h - световую отдачу, лм/Вт. Учитывая, что Фл = h Рл, формулу (1.9.1) приводим к виду:
![]() , (1.10.2)
, (1.10.2)
откуда
![]() , (1.10.3)
, (1.10.3)
Подставляя полученное выражение для Рл в формулу (1.10.1), находим выражение для удельной мощности:
![]() . (1.10.4)
. (1.10.4)
Такая форма записи удельной мощности показывает, что W зависит от тех же показателей, которые оказывают влияние на коэффициент использования Uoy. В табл. 1.10.1 - 1.10.9 приводятся данные об удельной мощности для светильников прямого сета с типовыми кривыми силами света.
1.10.2. Удельная мощность является важнейшим энергетическим показателем осветительной установки, широко используемым для оценки экономичности решений и для предварительного определения осветительной нагрузки на начальных стадиях проектирования, нормируемым МГСН 2.01-99.
Допускается для общего равномерного освещения вместо полного светотехнического расчета определять мощность и число ламп по таблицам удельной мощности. Не следует рассчитывать по таблицам удельной мощности освещение таких помещений, как гардеробы и санузлы, по существу, являющиеся локализованными. Таблицами удельной мощности необходимо пользоваться в пределах данных, для которых они составлены.
Таблица 1.10.1
УДЕЛЬНАЯ МОЩНОСТЬ ОБЩЕГО РАВНОМЕРНОГО ОСВЕЩЕНИЯ СВЕТИЛЬНИКАМИ С ЛН МОЩНОСТЬЮ 60 ВТ
|
h, м |
S, м2 |
Удельная мощность W, Вт/м2, светильников с КСС. Освещенность 100 лк; условный КПД = 100 %; rп = 0,5; rс = 0,3; rр = 0,1; Кз = 1,3; z = 1,15 |
|||||
|
Д-1 |
Д-2 |
Д-3 |
Г-1 |
Г-2 |
Г-3 |
||
|
1,5 - 2,0 |
10 - 15 |
24,6 |
23,5 |
23,0 |
19,8 |
17,4 |
16,9 |
|
15 - 25 |
23,9 |
21,5 |
20,1 |
17,6 |
15,8 |
15,6 |
|
|
25 - 50 |
21,1 |
19,5 |
17,6 |
15,8 |
14,7 |
14,4 |
|
|
50 - 150 |
17,8 |
16,2 |
15,3 |
14,1 |
13,3 |
13,2 |
|
|
150 - 300 |
16,2 |
15,1 |
14,4 |
13,6 |
13,1 |
13,1 |
|
|
Свыше 300 |
15,4 |
14,4 |
13,6 |
13,2 |
12,8 |
12,8 |
|
|
2,0 - 3,0 |
10 - 15 |
34,2 |
30,2 |
28,8 |
23,9 |
20,8 |
20,1 |
|
15 - 25 |
27,5 |
24,4 |
24,4 |
20,8 |
18,1 |
17,6 |
|
|
25 - 50 |
24,4 |
21,8 |
20,8 |
18,1 |
16,2 |
15,2 |
|
|
50 - 150 |
20,1 |
18,1 |
16,4 |
15,1 |
14,2 |
13,9 |
|
|
150 - 300 |
17,6 |
16,0 |
15,3 |
13,9 |
13,3 |
13,3 |
|
|
Свыше 300 |
15,4 |
14,4 |
13,6 |
13,2 |
12,8 |
12,8 |
|
|
3,0 - 4,0 |
10 - 15 |
60,3 |
48,7 |
39,6 |
31,7 |
26,4 |
25,3 |
|
15 - 20 |
45,2 |
38,4 |
33,3 |
26,9 |
22,6 |
22,2 |
|
|
20 - 30 |
34,2 |
30,2 |
28,8 |
23,9 |
20,4 |
20,1 |
|
|
30 - 50 |
27,5 |
24,4 |
24,4 |
20,8 |
18,1 |
17,7 |
|
|
50 - 120 |
23,5 |
21,1 |
19,8 |
17,3 |
15,6 |
15,4 |
|
|
120 - 300 |
20,1 |
17,8 |
16,4 |
14,9 |
14,1 |
14,1 |
|
|
Свыше 300 |
16,0 |
15,1 |
14,4 |
13,5 |
13,1 |
13,1 |
|
Таблица 1.10.2
УДЕЛЬНАЯ МОЩНОСТЬ ОБЩЕГО РАВНОМЕРНОГО ОСВЕЩЕНИЯ СВЕТИЛЬНИКАМИ С ЛН МОЩНОСТЬЮ 100 - 200 ВТ
|
h, м |
S, м2 |
Удельная мощность W, Вт/м2, светильников с КСС. Освещенность 100 лк; условный КПД = 100 %; rп = 0,5; rс = 0,3; rр = 0,1; Кз = 1,3; z = 1,15 |
|||||
|
Д-1 |
Д-2 |
Д-3 |
Г-1 |
Г-2 |
Г-3 |
||
|
2 - 3 |
10 - 15 |
28,8 |
25,4 |
24,3 |
20,1 |
17,5 |
16,9 |
|
15 - 25 |
23,2 |
20,5 |
20,5 |
17,5 |
15,2 |
14,8 |
|
|
25 - 50 |
20,5 |
18,4 |
17,5 |
15,2 |
13,7 |
13,3 |
|
|
50 - 150 |
16,9 |
15,2 |
13,9 |
12,7 |
12,0 |
11,7 |
|
|
150 - 300 |
14,8 |
13,2 |
12,9 |
11,7 |
11,2 |
11,2 |
|
|
Свыше 300 |
13,0 |
12,1 |
11,5 |
11,1 |
10,8 |
10,8 |
|
|
3 - 4 |
10 - 15 |
50,8 |
41,1 |
33,4 |
26,7 |
22,2 |
21,3 |
|
15 - 25 |
38,1 |
32,3 |
28,1 |
22,7 |
19,1 |
18,7 |
|
|
20 - 30 |
28,8 |
25,4 |
24,3 |
20,1 |
17,2 |
16,9 |
|
|
30 - 50 |
23,2 |
20,5 |
20,5 |
17,5 |
15,2 |
14,9 |
|
|
50 - 120 |
19,8 |
17,8 |
16,7 |
14,6 |
13,2 |
13,0 |
|
|
120 - 300 |
16,9 |
15,0 |
13,9 |
12,6 |
11,9 |
11,9 |
|
|
Свыше 300 |
13,5 |
12,7 |
12,1 |
11,4 |
11,0 |
11,0 |
|
|
4 - 6 |
10 - 17 |
97,1 |
62,8 |
53,4 |
36,8 |
28,1 |
28,8 |
|
17 - 25 |
59,3 |
46,4 |
38,1 |
28,8 |
23,7 |
23,7 |
|
|
25 - 35 |
42,7 |
38,1 |
30,5 |
24,3 |
20,5 |
20,9 |
|
|
35 - 50 |
33,3 |
28,8 |
26,0 |
21,3 |
18,4 |
18,1 |
|
|
50 - 80 |
24,3 |
22,2 |
22,2 |
18,7 |
16,2 |
15,7 |
|
|
80 - 150 |
21,8 |
19,4 |
18,7 |
16,2 |
14,4 |
14,0 |
|
|
150 - 400 |
18,4 |
16,4 |
15,2 |
13,7 |
12,6 |
12,3 |
|
|
Свыше 400 |
14,4 |
13,3 |
12,7 |
11,7 |
11,4 |
11,1 |
|
Таблица 1.10.3
УДЕЛЬНАЯ МОЩНОСТЬ ОБЩЕГО РАВНОМЕРНОГО ОСВЕЩЕНИЯ СВЕТИЛЬНИКАМИ С ЛН МОЩНОСТЬЮ 300 ВТ
|
h, м |
S, м2 |
Удельная мощность W, Вт/м2, светильников с КСС. Освещенность 100 лк; условный КПД = 100 %; rп = 0,5; rс = 0,3; rр = 0,1; Кз = 1,3; z = 1,15 |
||||||
|
Д-1 |
Д-2 |
Д-3 |
Г-1 |
Г-2 |
Г-3 |
|||
|
3 - 4 |
10 - 15 |
46,5 |
37,6 |
30,5 |
21,4 |
20,3 |
19,5 |
|
|
15 - 20 |
34,9 |
29,6 |
25,7 |
20,8 |
17,4 |
17,1 |
||
|
20 - 30 |
26,4 |
23,3 |
22,2 |
18,4 |
15,8 |
15,5 |
||
|
30 - 50 |
21,2 |
18,8 |
18,8 |
16,0 |
13,9 |
13,7 |
||
|
50 - 120 |
18,1 |
16,3 |
15,3 |
13,4 |
12,1 |
11,9 |
||
|
120 - 300 |
15,5 |
13,8 |
12,7 |
11,5 |
10,8 |
10,8 |
||
|
Свыше 300 |
12,4 |
11,6 |
11,1 |
10,4 |
10,1 |
10,1 |
||
|
4 - 6 |
10 - 17 |
88,8 |
57,5 |
48,8 |
33,7 |
25,7 |
26,4 |
|
|
17 - 25 |
54,3 |
42,5 |
34,9 |
26,4 |
21,7 |
21,7 |
||
|
25 - 35 |
39,1 |
34,9 |
27,9 |
22,2 |
18,8 |
19,2 |
||
|
35 - 50 |
30,5 |
25,4 |
23,8 |
19,5 |
16,8 |
16,6 |
||
|
50 - 80 |
22,2 |
20,4 |
20,4 |
17,1 |
14,8 |
14,4 |
||
|
80 - 150 |
19,9 |
17,8 |
17,1 |
14,8 |
13,2 |
12,8 |
||
|
150 - 400 |
16,8 |
15,0 |
14,0 |
12,5 |
11,5 |
11,2 |
||
|
Свыше 400 |
13,2 |
12,2 |
11,6 |
10,7 |
10,4 |
10,2 |
||
|
6 - 8 |
25 - 35 |
75,2 |
54,3 |
42,5 |
30,5 |
24,4 |
23,8 |
|
|
35 - 50 |
51,4 |
42,5 |
34,9 |
25,7 |
21,2 |
20,8 |
||
|
50 - 65 |
40,7 |
34,9 |
27,9 |
22,7 |
18,8 |
18,4 |
||
|
65 - 90 |
32,6 |
27,9 |
24,4 |
20,3 |
17,1 |
16,8 |
||
|
90 - 135 |
24,4 |
21,7 |
21,2 |
17,8 |
15,3 |
15,0 |
||
|
135 - 250 |
20,3 |
18,1 |
18,1 |
15,5 |
13,6 |
13,2 |
||
|
250 - 500 |
17,8 |
16,0 |
15,0 |
13,2 |
11,9 |
11,8 |
||
|
Свыше 500 |
13,2 |
12,2 |
11,6 |
10,7 |
10,4 |
10,2 |
||
Таблица 1.10.4
УДЕЛЬНАЯ МОЩНОСТЬ ОБЩЕГО РАВНОМЕРНОГО ОСВЕЩЕНИЯ СВЕТИЛЬНИКАМИ С ЛН МОЩНОСТЬЮ 500 ВТ
|
h, м |
S, м2 |
Удельная мощность W, Вт/м2, светильников с КСС. Освещенность 100 лк; условный КПД = 100 %; rп = 0,5; rс = 0,3; rр = 0,1; Кз = 1,3; z = 1,15 |
|||||
|
Д-1 |
Д-2 |
Д-3 |
Г-1 |
Г-2 |
Г-3 |
||
|
4 - 6 |
10 - 17 |
82,4 |
53,3 |
45,3 |
31,2 |
23,8 |
24,5 |
|
17 - 25 |
50,3 |
39,4 |
32,4 |
24,5 |
20,1 |
20,1 |
|
|
25 - 35 |
36,2 |
32,3 |
25,9 |
20,6 |
17,4 |
17,8 |
|
|
35 - 50 |
28,3 |
24,5 |
22,1 |
18,1 |
15,6 |
15,3 |
|
|
50 - 80 |
20,6 |
18,9 |
18,9 |
15,9 |
13,7 |
13,3 |
|
|
80 - 150 |
18,5 |
16,5 |
15,9 |
13,7 |
12,2 |
11,9 |
|
|
150 - 400 |
15,6 |
13,9 |
12,9 |
11,6 |
10,6 |
10,4 |
|
|
Свыше 400 |
12,2 |
11,3 |
10,8 |
9,9 |
9,6 |
9,4 |
|
|
6 - 8 |
25 - 35 |
69,7 |
50,3 |
39,4 |
28,3 |
22,6 |
22,1 |
|
35 - 50 |
47,7 |
39,4 |
32,4 |
23,8 |
19,7 |
19,3 |
|
|
50 - 65 |
37,8 |
32,3 |
25,9 |
21,1 |
17,4 |
17,1 |
|
|
65 - 90 |
30,2 |
25,9 |
22,6 |
18,9 |
15,9 |
15,6 |
|
|
90 - 135 |
22,6 |
20,1 |
19,7 |
16,5 |
14,2 |
13,9 |
|
|
135 - 250 |
18,9 |
16,8 |
16,8 |
14,4 |
12,6 |
12,2 |
|
|
250 - 500 |
16,5 |
14,8 |
13,9 |
12,2 |
11,0 |
10,9 |
|
|
Свыше 500 |
12,2 |
11,3 |
10,8 |
10,0 |
9,6 |
9,4 |
|
|
8 - 12 |
50 - 70 |
78,8 |
50,3 |
43,1 |
29,2 |
23,8 |
22,6 |
|
70 - 100 |
50,3 |
39,4 |
32,3 |
24,5 |
20,1 |
19,7 |
|
|
100 - 130 |
39,4 |
32,4 |
26,6 |
21,1 |
17,8 |
17,1 |
|
|
130 - 200 |
28,3 |
24,5 |
22,1 |
18,1 |
15,6 |
15,4 |
|
|
200 - 300 |
21,6 |
18,9 |
18,9 |
15,9 |
13,9 |
13,5 |
|
|
300 - 600 |
18,5 |
16,5 |
16,2 |
13,9 |
12,2 |
11,9 |
|
|
600 - 1500 |
15,6 |
14,2 |
13,1 |
11,8 |
10,8 |
10,6 |
|
|
Свыше 1500 |
12,2 |
11,3 |
10,8 |
10,0 |
9,6 |
9,4 |
|
Таблица 1.10.5
УДЕЛЬНАЯ МОЩНОСТЬ ОБЩЕГО РАВНОМЕРНОГО ОСВЕЩЕНИЯ СВЕТИЛЬНИКАМИ С ЛН МОЩНОСТЬЮ 1000 ВТ
|
h, м |
S, м2 |
Удельная мощность W, Вт/м2, светильников с КСС. Освещенность 100 лк; условный КПД = 100 %; rп = 0,5; rс = 0,3; rр = 0,1; Кз = 1,3; z = 1,15 |
|||||||
|
Д-1 |
Д-2 |
Д-3 |
Г-1 |
Г-2 |
Г-3 |
К-1 |
К-2 |
||
|
4 - 6 |
10 - 17 |
75,5 |
49,0 |
41,6 |
28,7 |
21,9 |
22,4 |
18,9 |
16,6 |
|
17 - 25 |
46,1 |
36,1 |
29,7 |
22,5 |
18,5 |
18,5 |
16,3 |
14,3 |
|
|
25 - 35 |
33,3 |
29,7 |
23,7 |
18,9 |
16,0 |
16,3 |
14,3 |
13,0 |
|
|
35 - 50 |
26,0 |
22,5 |
20,3 |
16,6 |
14,3 |
14,1 |
13,0 |
11,9 |
|
|
50 - 80 |
18,9 |
17,3 |
17,3 |
14,6 |
12,6 |
12,2 |
11,7 |
10,9 |
|
|
80 - 150 |
17,0 |
15,1 |
14,6 |
12,6 |
11,2 |
10,9 |
10,8 |
9,9 |
|
|
150 - 400 |
14,3 |
12,8 |
11,9 |
10,7 |
9,8 |
9,6 |
9,6 |
9,1 |
|
|
Свыше |
11,2 |
10,4 |
9,9 |
9,1 |
8,9 |
8,6 |
8,8 |
8,5 |
|
|
6 - 8 |
25 - 35 |
64,0 |
46,2 |
96,2 |
26,0 |
20,8 |
20,3 |
18,5 |
16,0 |
|
35 - 50 |
43,8 |
36,2 |
29,6 |
21,9 |
18,1 |
17,7 |
16,0 |
14,3 |
|
|
50 - 65 |
34,7 |
29,7 |
23,7 |
19,4 |
16,0 |
15,7 |
14,3 |
13,0 |
|
|
65 - 90 |
27,8 |
23,7 |
20,8 |
17,3 |
14,6 |
14,3 |
13,2 |
12,0 |
|
|
90 - 135 |
20,8 |
18,5 |
18,1 |
15,1 |
13,0 |
12,8 |
12,2 |
11,2 |
|
|
135 - 250 |
17,4 |
15,4 |
15,4 |
13,2 |
11,5 |
11,2 |
10,9 |
10,1 |
|
|
250 - 500 |
15,1 |
13,6 |
12,8 |
11,2 |
10,1 |
10,0 |
10,0 |
9,3 |
|
|
Свыше |
11,2 |
10,4 |
9,9 |
9,1 |
8,9 |
8,6 |
8,8 |
8,5 |
|
|
8 - 12 |
50 - 70 |
72,3 |
46,2 |
39,6 |
26,8 |
21,9 |
20,8 |
18,9 |
16,3 |
|
70 - 100 |
46,2 |
36,1 |
29,7 |
22,4 |
18,5 |
18,1 |
16,3 |
14,3 |
|
|
100 - 130 |
36,1 |
29,7 |
24,4 |
19,3 |
16,3 |
15,7 |
14,3 |
13,2 |
|
|
130 - 200 |
26,0 |
22,4 |
20,2 |
16,6 |
14,3 |
14,1 |
13,0 |
11,7 |
|
|
200 - 300 |
19,8 |
17,3 |
17,3 |
14,6 |
12,8 |
12,4 |
11,9 |
10,9 |
|
|
300 - 600 |
16,9 |
15,1 |
14,8 |
12,8 |
11,2 |
10,9 |
10,8 |
10,0 |
|
|
600 - 1500 |
14,3 |
13,0 |
12,0 |
10,8 |
9,9 |
9,8 |
9,7 |
9,1 |
|
|
Свыше |
11,2 |
10,4 |
9,9 |
9,1 |
8,8 |
8,6 |
8,7 |
8,5 |
|
Таблица 1.10.6
УДЕЛЬНАЯ МОЩНОСТЬ ОБЩЕГО РАВНОМЕРНОГО ОСВЕЩЕНИЯ СВЕТИЛЬНИКАМИ С ЛП ТИПА ЛБ40
|
h, м |
S, м2 |
Удельная мощность W, Вт/м2, светильников с КСС. Освещенность 100 лк; условный КПД = 100 %; Кз = 1,5; z = 1,1 |
|||||||||
|
Д-1 |
Д-2 |
Д-3 |
Г-1 |
||||||||
|
при rп, rс, rр |
|||||||||||
|
0,7; 0,5; 0,1 |
0,5; 0,3; 0,1 |
0,7; 0,5; 0,1 |
0,5; 0,3; 0,1 |
0,7; 0,5; 0,1 |
0,5; 0,3; 0,1 |
0,7; 0,5; 0,1 |
0,5; 0,3; 0,1 |
||||
|
2 - 3 |
10 - 15 |
4,9 |
6,1 |
4,4 |
5,2 |
4,3 |
5,0 |
3,7 |
4,1 |
||
|
15 - 25 |
4,0 |
4,8 |
3,7 |
4,2 |
3,7 |
4,2 |
3,3 |
3,6 |
|||
|
25 - 50 |
3,6 |
4,2 |
3,3 |
3,8 |
3,2 |
3,6 |
2,9 |
3,1 |
|||
|
50 - 150 |
3,1 |
3,5 |
2,8 |
3,1 |
2,7 |
2,9 |
2,5 |
2,6 |
|||
|
150 - 300 |
2,7 |
3,0 |
2,6 |
2,8 |
2,5 |
2,6 |
2,4 |
2,5 |
|||
|
Свыше 300 |
2,5 |
2,7 |
2,4 |
2,5 |
2,3 |
2,5 |
2,2 |
2,3 |
|||
|
3 - 4 |
10 - 15 |
7,6 |
10,5 |
6,7 |
8,5 |
5,6 |
4,9 |
6,9 |
5,5 |
||
|
15 - 20 |
7,8 |
5,4 |
6,7 |
4,9 |
5,8 |
4,2 |
4,7 |
4,7 |
|||
|
20 - 30 |
4,9 |
5,9 |
4,4 |
5,2 |
4,2 |
5,0 |
3,7 |
4,2 |
|||
|
30 - 50 |
4,0 |
3,7 |
4,6 |
3,7 |
3,7 |
4,2 |
3,2 |
3,6 |
|||
|
50 - 120 |
3,5 |
4,1 |
3,2 |
3,7 |
3,1 |
3,4 |
2,8 |
3,0 |
|||
|
120 - 300 |
3,0 |
3,5 |
2,8 |
3,1 |
2,7 |
2,9 |
2,5 |
2,6 |
|||
|
Свыше 300 |
2,6 |
2,8 |
2,5 |
2,6 |
2,4 |
2,3 |
2,2 |
2,3 |
|||
|
4- 6 |
10 - 17 |
10,5 |
20,0 |
9,6 |
12,9 |
8,1 |
11,0 |
6,3 |
7,6 |
||
|
17 - 25 |
8,5 |
12,2 |
7,1 |
9,6 |
6,5 |
7,8 |
5,1 |
5,9 |
|||
|
25 - 35 |
7,1 |
8,8 |
5,9 |
7,8 |
5,1 |
6,3 |
4,4 |
5,0 |
|||
|
35 - 50 |
5,5 |
6,9 |
4,9 |
5,9 |
4,5 |
5,4 |
3,8 |
4,4 |
|||
|
50 - 80 |
4,2 |
5,0 |
3,8 |
4,6 |
4,0 |
4,6 |
3,4 |
3,8 |
|||
|
80 - 150 |
3,8 |
4,5 |
3,4 |
4,0 |
3,4 |
3,8 |
3,1 |
3,3 |
|||
|
150 - 400 |
3,3 |
3,5 |
3,1 |
3,4 |
2,9 |
3,1 |
2,6 |
2,8 |
|||
|
Свыше 400 |
2,7 |
3,0 |
2,6 |
2,8 |
2,5 |
2,6 |
2,3 |
2,4 |
|||
Таблица 1.10.7
УДЕЛЬНАЯ МОЩНОСТЬ ОБЩЕГО РАВНОМЕРНОГО ОСВЕЩЕНИЯ СВЕТИЛЬНИКАМИ С ЛАМПАМИ ТИПА ДРЛ
|
h, м |
S, м2 |
Удельная мощность W, Вт/м2, светильников с КСС. Освещенность 100 лк; условный КПД = 100 %; rп = 0,5; rс = 0,3; rр = 0,1; Кз = 1,5; z = 1,15 |
|||||||
|
Д-1 |
Д-2 |
Д-3 |
Г-1 |
Г-2 |
Г-3 |
К-1 |
К-2 |
||
|
3 - 4 |
10 - 15 |
14,9 |
12,0 |
9,8 |
7,8 |
6,5 |
- |
- |
- |
|
15 - 20 |
11,2 |
9,5 |
8,2 |
6,7 |
5,6 |
- |
- |
- |
|
|
20 - 30 |
8,5 |
7,4 |
7,1 |
5,9 |
5,0 |
- |
- |
- |
|
|
30 - 50 |
6,8 |
6,0 |
6,0 |
5,1 |
4,5 |
- |
- |
- |
|
|
50 - 120 |
5,8 |
5,2 |
4,9 |
4,3 |
3,9 |
- |
- |
- |
|
|
120 - 300 |
4,9 |
4,4 |
4,1 |
3,7 |
3,5 |
- |
- |
- |
|
|
Свыше 300 |
3,9 |
3,7 |
3,5 |
3,4 |
3,2 |
- |
- |
- |
|
|
4 - 6 |
10 - 17 |
28,5 |
18,4 |
15,7 |
10,8 |
8,2 |
8,5 |
- |
- |
|
17 - 25 |
17,4 |
13,6 |
11,2 |
8,5 |
7,0 |
7,0 |
- |
- |
|
|
25 - 35 |
12,5 |
11,2 |
8,9 |
7,1 |
6,0 |
6,1 |
- |
- |
|
|
35 - 50 |
9,8 |
8,5 |
7,6 |
6,2 |
5,4 |
5,3 |
- |
- |
|
|
50 - 80 |
7,1 |
6,5 |
6,5 |
5,5 |
4,7 |
4,6 |
- |
- |
|
|
80 - 150 |
6,4 |
5,7 |
5,5 |
4,7 |
4,2 |
4,1 |
- |
- |
|
|
150 - 400 |
5,4 |
4,8 |
4,5 |
4,0 |
3,7 |
3,6 |
- |
- |
|
|
Свыше 400 |
4,2 |
3,9 |
3,7 |
3,4 |
3,3 |
3,3 |
- |
- |
|
|
6 - 8 |
50 - 65 |
13,0 |
11,2 |
9,0 |
7,3 |
6,0 |
5,9 |
5,4 |
- |
|
65 - 90 |
10,4 |
8,9 |
7,8 |
6,5 |
5,5 |
5,4 |
5,0 |
- |
|
|
90 - 135 |
7,8 |
6,9 |
6,8 |
5,7 |
4,9 |
4,8 |
4,6 |
- |
|
|
135 - 250 |
6,5 |
5,8 |
5,8 |
5,0 |
4,3 |
4,2 |
4,1 |
- |
|
|
250 - 500 |
5,7 |
5,1 |
4,8 |
4,2 |
3,8 |
3,8 |
3,8 |
- |
|
|
Свыше 500 |
4,2 |
3,9 |
3,7 |
3,4 |
3,3 |
3,8 |
3,3 |
- |
|
|
6 - 12 |
70 - 100 |
17,4 |
13,6 |
11,2 |
8,5 |
7,0 |
6,8 |
6,1 |
- |
|
100 - 130 |
13,6 |
11,2 |
9,2 |
7,3 |
6,1 |
5,9 |
5,4 |
- |
|
|
130 - 200 |
9,8 |
8,5 |
7,6 |
6,3 |
5,4 |
5,3 |
4,9 |
- |
|
|
200 - 300 |
7,5 |
6,5 |
6,5 |
5,5 |
4,8 |
4,7 |
4,4 |
- |
|
|
300 - 600 |
6,4 |
5,7 |
5,6 |
4,8 |
4,2 |
4,1 |
4,1 |
- |
|
|
600 - 1500 |
5,4 |
4,9 |
4,5 |
4,1 |
3,7 |
3,7 |
3,6 |
- |
|
|
Свыше 1500 |
4,2 |
3,9 |
3,7 |
3,4 |
3,3 |
3,3 |
3,3 |
- |
|
|
12 - 16 |
130 - 200 |
- |
13,6 |
11,2 |
8,4 |
7,0 |
6,8 |
6,3 |
5,4 |
|
200 - 350 |
- |
9,5 |
8,0 |
6,8 |
5,7 |
5,5 |
5,1 |
4,6 |
|
|
350 - 600 |
- |
6,6 |
6,7 |
5,6 |
4,8 |
4,7 |
4,5 |
4,2 |
|
|
600 - 1300 |
- |
5,6 |
5,4 |
4,7 |
4,2 |
4,1 |
4,0 |
3,7 |
|
|
1300 - 4000 |
- |
4,6 |
4,3 |
3,8 |
3,6 |
3,5 |
3,5 |
3,3 |
|
|
Свыше 4000 |
- |
3,9 |
3,7 |
3,4 |
3,3 |
3,3 |
3,3 |
3,2 |
|
Таблица 1.10.8
УДЕЛЬНАЯ МОЩНОСТЬ ОБЩЕГО РАВНОМЕРНОГО ОСВЕЩЕНИЯ СВЕТИЛЬНИКАМИ С ЛАМПАМИ ТИПА ДРИ
|
h, м |
S, м2 |
Удельная мощность W, Вт/м2, светильников с КСС. Освещенность 100 лк; условный КПД = 100 %; rп = 0,5; rс = 0,3; rр = 0,1; Кз = 1,5; z = 1,15 |
|||||||
|
Д-1 |
Д-2 |
Д-3 |
Г-1 |
Г-2 |
Г-3 |
К-1 |
К-2 |
||
|
3 - 4 |
10 - 15 |
9,7 |
7,8 |
6,3 |
5,1 |
4,2 |
4,0 |
- |
- |
|
15 - 20 |
7,2 |
6,1 |
5,3 |
4,3 |
3,6 |
3,6 |
- |
- |
|
|
20 - 30 |
5,5 |
4,8 |
4,6 |
3,8 |
3,3 |
3,2 |
- |
- |
|
|
30 - 50 |
4,4 |
3,9 |
3,9 |
3,3 |
2,9 |
2,8 |
- |
- |
|
|
50 - 120 |
3,7 |
3,4 |
3,2 |
2,8 |
2,5 |
2,5 |
- |
- |
|
|
120 - 300 |
3,2 |
2,8 |
2,6 |
2,4 |
2,2 |
2,2 |
- |
- |
|
|
Свыше 300 |
2,6 |
2,4 |
2,3 |
2,2 |
2,1 |
2,1 |
- |
- |
|
|
4 - 6 |
10 - 17 |
18,4 |
11,9 |
10,1 |
7,0 |
5,3 |
5,5 |
- |
- |
|
17 - 25 |
11,3 |
8,8 |
7,2 |
5,5 |
4,5 |
4,5 |
- |
- |
|
|
25 - 35 |
8,1 |
7,2 |
5,8 |
4,6 |
3,9 |
4,0 |
- |
- |
|
|
35 - 50 |
6,3 |
5,5 |
4,9 |
4,1 |
3,5 |
3,4 |
- |
- |
|
|
50 - 80 |
4,6 |
4,2 |
4,2 |
3,6 |
3,1 |
3,0 |
- |
- |
|
|
80 - 150 |
4,1 |
3,7 |
3,6 |
3,1 |
2,7 |
2,7 |
- |
- |
|
|
150 - 400 |
3,5 |
3,1 |
2,9 |
2,6 |
2,4 |
2,3 |
- |
- |
|
|
Свыше 400 |
2,7 |
2,5 |
2,4 |
2,2 |
2,2 |
2,1 |
- |
- |
|
|
6 - 8 |
50- 65 |
8,4 |
7,2 |
5,8 |
4,7 |
3,9 |
3,8 |
3,5 |
- |
|
65 - 90 |
6,8 |
5,8 |
5,1 |
4,2 |
3,6 |
3,5 |
3,2 |
- |
|
|
90 - 135 |
5,1 |
4,5 |
4,4 |
3,7 |
3,2 |
3,1 |
3,0 |
- |
|
|
135 - 250 |
4,2 |
3,8 |
3,8 |
3,2 |
2,8 |
2,7 |
2,7 |
- |
|
|
250 - 500 |
3,7 |
3,3 |
3,1 |
2,7 |
2,5 |
2,4 |
2,4 |
- |
|
|
Свыше 500 |
2,7 |
2,5 |
2,4 |
2,2 |
2,2 |
2,1 |
2,1 |
- |
|
|
6 - 12 |
70 - 100 |
11,8 |
8,8 |
7,2 |
5,5 |
4,5 |
4,4 |
4,0 |
- |
|
100 - 130 |
8,2 |
7,2 |
6,0 |
4,7 |
4,0 |
3,8 |
3,5 |
- |
|
|
130 - 200 |
6,3 |
5,5 |
4,9 |
4,0 |
3,5 |
3,4 |
3,2 |
- |
|
|
200 - 300 |
4,8 |
4,2 |
4,2 |
3,6 |
3,1 |
3,0 |
2,9 |
- |
|
|
300 - 600 |
4,1 |
3,7 |
3,8 |
3,4 |
2,7 |
2,7 |
2,6 |
- |
|
|
600 - 1500 |
3,5 |
3,2 |
2,9 |
2,6 |
2,4 |
2,4 |
2,3 |
- |
|
|
Свыше 1500 |
2,7 |
2,4 |
2,4 |
2,2 |
2,1 |
2,1 |
2,1 |
3,5 |
|
|
12 - 16 |
150 - 200 |
- |
8,8 |
7,2 |
5,5 |
4,5 |
4,4 |
4,1 |
3,0 |
|
200 - 350 |
- |
6,1 |
5,2 |
4,4 |
3,7 |
3,6 |
3,3 |
2,7 |
|
|
350 - 600 |
- |
4,3 |
4,8 |
3,6 |
3,4 |
3,0 |
2,9 |
2,4 |
|
|
600 - 1300 |
- |
3,6 |
3,5 |
3,0 |
2,7 |
2,8 |
2,6 |
2,2 |
|
|
1300 - 4000 |
- |
3,0 |
2,5 |
2,5 |
2,3 |
2,3 |
2,3 |
2,1 |
|
|
Свыше 4000 |
- |
2,5 |
2,2 |
2,2 |
2,1 |
2,1 |
2,1 |
- |
|
Таблица 1.10.9
УДЕЛЬНАЯ МОЩНОСТЬ ОБЩЕГО РАВНОМЕРНОГО ОСВЕЩЕНИЯ СВЕТИЛЬНИКАМИ С ЛАМПАМИ ТИПА ДНаТ
|
h, м |
S, м2 |
Удельная мощность W, Вт/м2, светильников с КСС. Освещенность 100 лк; условный КПД = 100 %; rп = 0,5; rс = 0,3; rр = 0,1; Кз = 1,5; z = 1,15 |
|||||||
|
Д-1 |
Д-2 |
Д-3 |
Г-1 |
Г-2 |
Г-3 |
К-1 |
К-2 |
||
|
3 - 4 |
10 - 15 |
9,1 |
7,4 |
6,0 |
4,8 |
3,8 |
3,8 |
- |
- |
|
15 - 20 |
6,8 |
5,8 |
5,0 |
4,1 |
3,4 |
3,4 |
- |
- |
|
|
20 - 30 |
5,2 |
4,6 |
4,4 |
3,6 |
3,1 |
3,0 |
- |
- |
|
|
30 - 50 |
4,2 |
4,0 |
3,7 |
3,1 |
2,7 |
2,7 |
- |
- |
|
|
50 - 120 |
3,5 |
3,2 |
3,0 |
2,6 |
2,4 |
2,3 |
- |
- |
|
|
120 - 300 |
3,0 |
2,7 |
2,5 |
2,3 |
2,1 |
2,1 |
- |
- |
|
|
Свыше 300 |
2,4 |
2,2 |
2,0 |
2,0 |
2,0 |
2,0 |
- |
- |
|
|
4 - 6 |
10 - 17 |
17,4 |
11,3 |
9,6 |
6,6 |
5,0 |
5,2 |
- |
- |
|
17 - 25 |
10,6 |
8,3 |
6,8 |
5,2 |
4,3 |
4,3 |
- |
- |
|
|
25 - 35 |
7,7 |
6,8 |
5,5 |
4,4 |
3,7 |
3,8 |
- |
- |
|
|
35 - 50 |
6,0 |
5,2 |
4,7 |
3,8 |
3,3 |
3,2 |
- |
- |
|
|
50 - 80 |
4,3 |
4,0 |
4,0 |
3,4 |
2,9 |
2,8 |
- |
- |
|
|
80 - 150 |
3,9 |
3,5 |
3,4 |
2,9 |
2,6 |
2,5 |
- |
- |
|
|
150 - 400 |
3,3 |
2,9 |
2,7 |
2,5 |
2,3 |
2,2 |
- |
- |
|
|
Свыше 400 |
2,6 |
2,4 |
2,3 |
2,1 |
2,0 |
2,0 |
- |
- |
|
|
6 - 8 |
50 - 65 |
8,0 |
6,8 |
5,5 |
4,5 |
3,7 |
3,6 |
3,3 |
- |
|
65 - 90 |
6,4 |
5,5 |
4,8 |
4,0 |
3,4 |
3,3 |
3,0 |
- |
|
|
90 - 135 |
4,8 |
4,3 |
4,2 |
3,5 |
3,0 |
2,9 |
2,8 |
- |
|
|
135 - 250 |
4,0 |
3,5 |
3,5 |
3,0 |
2,7 |
2,6 |
2,5 |
- |
|
|
250 - 500 |
3,5 |
3,1 |
2,9 |
2,6 |
2,3 |
2,3 |
2,3 |
- |
|
|
Свыше 500 |
2,6 |
2,4 |
2,3 |
2,1 |
2,0 |
2,0 |
2,0 |
- |
|
|
8 - 12 |
70 - 100 |
10,6 |
8,3 |
6,8 |
5,2 |
4,3 |
4,2 |
3,8 |
- |
|
100 - 130 |
8,3 |
6,8 |
5,6 |
4,5 |
3,8 |
3,6 |
3,3 |
- |
|
|
130 - 200 |
6,0 |
5,2 |
4,7 |
3,8 |
3,3 |
3,2 |
3,0 |
- |
|
|
200 - 300 |
4,6 |
4,0 |
4,0 |
3,4 |
2,9 |
2,9 |
2,7 |
- |
|
|
300 - 600 |
3,9 |
3,5 |
3,4 |
2,9 |
2,6 |
2,5 |
2,5 |
- |
|
|
600 - 1500 |
3,3 |
3,0 |
2,8 |
2,5 |
2,3 |
2,2 |
2,2 |
- |
|
|
Свыше 1500 |
2,6 |
2,4 |
2,3 |
2,1 |
2,0 |
2,0 |
2,0 |
- |
|
1.103. При пользовании таблицами (1.10.1 - 1.10.9) следует учитывать следующие особенности:
- если коэффициент запаса, принятый для расчета, отличается от указанных в соответствующей таблице, то допускается пропорциональный перерасчет удельной мощности.
- табличные значения удельной мощности соответствуют номинальному напряжению 220 В.
- в таблицах приведены W для условного КПД = 100%; расчетное значение W для освещенности 100 лк от реально применяемых светильников определяется делением табличного значения W100% на выраженный в долях единицы КПД светильников.
- при составлении таблиц удельной мощности не учитывалась форма помещения и коэффициент использования определялся по формуле:
![]() , (1.10.5)
, (1.10.5)
- что является достаточно точным при А/В £ 3.
Приводимые в таблицах W для Е = 100 лк изменяются пропорционально при рассчитываемых ЕН.
Табл. 1.10.1 - 1.10.9 рассчитывались для светильников прямого света при отношении расстояний между ними или между их рядами к высоте подвеса L : h = 0,4 для КСС типов Г-3, К-1, К-2; L : h = 1,0 для КСС типов Д-3, Г-1, Г-2 и L : h = 1,5 для КСС типов Д-1, Д-2, а также при полном совпадении данных, для которых составлены эти таблицы.
Порядок расчета по удельной мощности при лампах накаливания и лампах типа ДРЛ:
- определяется hp, тип и число светильников п в помещении;
- по таблицам МГСН 2.06-99 находится нормированная освещенность для данного вида помещений ЕН;
- по соответствующей таблице находится удельная мощность W;
- определяется мощность лампы по формуле:
Pл = WS/n, (1.10.6)
и подбирается ближайшая стандартная лампа.
Если расчетная мощность лампы оказывается большей, чем в принятых светильниках, следует определить необходимое число светильников, приняв мощность лампы, приемлемую для данного светильника.
1.10.4. При применении светильников с люминесцентными лампами сохраняется прежний порядок расчета освещения помещений, включая определение числа рядов светильников N и типа лампы.
- По соответствующей таблице находится удельная мощность W для ламп данной мощности или нескольких возможных к применению мощностей.
- Определяется необходимое число светильников в ряду:
n = WS/Pл, (1.10.7)
и осуществляется их компоновка.
Пример. В помещении площадью S = A ´ В = 16 ´10 = 160 м2 с rп = 0,5; rс = 0,3; rр = 0,1 на расчетной высоте hр = 3,2 м предполагается установить светильники типа ЛСП02-2´40-10 (КСС типа Д-3, КПД - 60%) с ЛЛ типа ЛБ. Определить число светильников, необходимое для создания освещенности Е = 300 лк при коэффициенте запаса Кз = 1,8 и коэффициенте неравномерности z = 1,1.
По табл. 1.10.6 находится W100% = 2,9 Вт/м2. Но так как в табл. 1.10.6 Е = 100 лк; Кз = 1,5 и КПД = 100%, пропорциональным пересчетом определяется значение:
![]() .
.
Число светильников
n = WS/Pл = (17,4×160)/80 » 35 шт.
Таким образом, предусматривается 3 ряда по 12 светильников в каждом.
1.11. Инженерный метод расчета качественных показателей осветительных установок
Коэффициент пульсации
1.11.1. Коэффициент пульсации светового потока источников света определяется по формуле.
![]() , (1.11.1)
, (1.11.1)
где Фmax и Фmin - соответственно максимальное и минимальное значения светового потока за период колебания; Фср - среднее значение светового потока за тот же период.
Значения Кп.и для наиболее распространенных источников света приведены в табл. 1.11.1 и 1.11.2.
Как видно из табл. 1.11.1, 1.11.2, ограничение значений Кп.и может быть достигнуто применением специальных схем включения источников света в светильнике или расфазированием светильников в ОУ.
Таблица 1.11.1
|
Значение Кп.и, % от |
||||
|
одной лампы |
установленных в одной световой точке |
|||
|
двух ламп при схеме питания отстающим и опережающим током |
двух ламп, питаемых от разных фаз |
трех ламп, питаемых от разных фаз |
||
|
ЛБ, ЛТБ |
25 |
10,5 |
10 |
2,2 |
|
ЛХБ |
35 |
15 |
15 |
3,1 |
|
ЛДЦ |
40 |
17 |
17 |
3,5 |
|
ЛД |
55 |
23 |
23 |
5,0 |
Таблица 1.11.2
|
Значение Кп.и, % от |
|||
|
одной лампы |
установленных в одной световой точке |
||
|
двух ламп, питаемых от разных фаз |
трех ламп, питаемых от равных фаз |
||
|
ДРЛ |
65 |
32 |
5,2 |
|
ДРИ (двухкомпонентные) |
45 |
23 |
3,5 |
|
ДНаТ |
80 |
39,5 |
6,3 |
|
ДКсТ |
130 |
65 |
5,0 |
Этими же средствами обеспечивается ограничение коэффициента пульсации освещенности Кп на рабочих местах, определяемого по формуле:
где Еmax и Еmin - соответственно, максимальное и минимальное значения освещенности за период колебания; Еср - среднее значение освещенности за тот же период.
Таблица 1.11.3
|
Нормированное значение Кп, %, не более |
||||
|
10 |
15 |
20 |
30 |
|
|
При любом расположения светильников: число ламп в светильнике, кратное трем, с равномерным распределением между фазами сети |
+ |
+ |
+ |
+ |
|
Число ламп в светильнике, кратное двум, с включением половины ламп по схеме опережающего и половины - по схеме отстающего тока: |
|
|
|
|
|
лампы ЛБ и ЛТБ |
+ |
+ |
+ |
+ |
|
лампы ЛХБ |
- |
+ |
+ |
+ |
|
лампы ЛДЦ |
- |
- |
+ |
+ |
|
лампы ЛД |
- |
- |
+ |
+ |
|
Любое число ламп в светильнике и любая схема включения: лампы ЛБ и ЛТБ |
- |
- |
- |
+ |
|
При сплошных линиях светильников и высоте подвеса hp ³ 2 м трехфазные линии с поочередным включением светильников на разные фазы сети |
|
|
|
|
|
любые лампы и схемы |
|
|
|
|
|
то же, но двухфазные линии: |
+ |
+ |
+ |
+ |
|
лампы ЛБ и ЛТБ |
+ |
+ |
+ |
+ |
|
лампы ЛХБ |
- |
+ |
+ |
+ |
|
лампы ЛДЦ и ЛД |
- |
- |
+ |
+ |
|
Двухфазные линии с поочередным включением светильников на разные фазы сети, число ламп в светильнике, кратное двум, с включением половины ламп по схеме опережающего и половины - по схеме отстающего тока, лампы всех типов |
+ |
+ |
+ |
+ |
* Условия, при которых соблюдаются нормированные значения коэффициента пульсации, отмечены знаком «+».
Ограничение Кп достигается:
в двух- и четырехламповых светильниках с ЛЛ применением компенсированных пускорегулирующих аппаратов (ПРА), когда питание одной половины ламп в светильнике осуществляется отстающим током, а другой половины - опережающим;
поочередным присоединением соседних светильников в ряду или соседних рядов к разным фазам сети;
установкой в одной световой точке двух или трех светильников с ГЛВД типов ДРЛ, ДРИ, ДнаТ, присоединенных к разным фазам сети;
питанием различных ламп в многоламповых светильниках с ЛЛ от разных фаз сети.
В табл. 1.11.3 приведены условия, при которых нормированные значения Кп соблюдаются, и проверка их выполнения в ОУ с ЛЛ не требуется.
1.11.2. Для наиболее распространенных светильников с ГЛВД типа ДРЛ в табл. 1.11.4 и 1.11.5 указаны различные случаи расположения и расфазировки светильников и предельные значения отношения расстояния между светильниками lсв к расчетной высоте hp, при которых соблюдаются нормированные значения Кп (через b, в таблице обозначено расстояние между рядами светильников; если численное значение величины lсв/hр приведено в виде дроби, то числитель относится к полям прямоугольной формы, а знаменатель - к шахматному расположению светильников).
В случаях, не указанных в табл. 1.11.3 - 1.11.5, производится вычисление значения Ки в той точке расположения рабочих мест, где Кп имеет максимальное значение. Для этого в указанной точке отдельно определяются относительные освещенности, создаваемые светильниками, питаемыми от каждой из трех фаз.
Таблица 1.11.4
|
Количество светильников в световой точке, подключенных к разным фазам |
Нормированное значение Кп % не более |
||||
|
10 |
15 |
20 |
30 |
||
|
ДРЛ |
2 |
- |
- |
- |
+ |
|
3 |
+ |
+ |
+ |
+ |
|
|
ДРИ (двухкомпонентная) |
2 |
- |
- |
- |
+ |
|
3 |
+ |
+ |
+ |
+ |
|
|
ДнаТ |
2 |
- |
- |
- |
- |
|
3 |
+ |
+ |
+ |
+ |
|
Примечание. То же, что к табл. 1.11.3.
Таблица 1.11.5
|
Расположение и расфазировка светильников |
b/hp |
Наибольшие значения lсв/hp, при которых обеспечивается Кп, % не более |
||||||
|
10 |
15 |
20 |
30 |
|||||
|
Светильники с типовой кривой Д (СД2, УПД и т.д.) |
||||||||
|
1 |
Одиночные светильники |
- |
0,45 |
0,6 |
0,7 |
0,9 |
||
|
А-В-С-А-В-С |
||||||||
|
Сдвоенные светильники |
- |
0,8 |
1,1 |
1,3 |
1,8 |
|||
|
АВ-СА-ВС-АВ-СА-ВС |
||||||||
|
2 и более |
Одиночные светильники: |
0,3 |
0,7/0,9 |
1,0/1,1 |
1,2/1,4 |
1,8 |
||
|
первый ряд |
0,6 |
0,6 |
0,9 |
1,1 |
1,6 |
|||
|
А-В-С-А-В-С |
0,9 |
0,35/0,5 |
0,7 |
0,95 |
1,2/1,3 |
|||
|
второй ряд |
1,2 |
0,3/0,5 |
0,65 |
0,8 |
1,1 |
|||
|
В-С-А-В-С-А |
1,8 |
0,2/0,45 |
0,6 |
0,75 |
1,0 |
|||
|
Сдвоенные светильники: |
0,3 |
0,8/0,4 |
1,2/1,4 |
1,8 |
1,8 |
|||
|
первый ряд |
0,6 |
0,8/0,4 |
1,2 |
1,8 |
1,8 |
|||
|
АВ-СА-ВС-АВ-СА-ВС |
0,9 |
0,8/0,4 |
1,15 |
1,7/1,8 |
1,8 |
|||
|
второй ряд |
1,2 |
0,8/0,4 |
1,1 |
1,6/1,7 |
1,8 |
|||
|
ВС-АВ-СА-ВС-АВ-СА |
1,8 |
0,8/0,4 |
1,1 |
1,4/1,6 |
1,8 |
|||
|
Светильники с типовой кривой Г (ГсР, С34 и т.д.) |
||||||||
|
1 |
Одиночные светильники: |
- |
0,45 |
0,5 |
0,6 |
0,7 |
||
|
А-В-С-А-В-С |
||||||||
|
Сдвоенные светильники: |
- |
0,55 |
0,75 |
0,95 |
1,2 |
|||
|
АВ-СА-ВС-АВ-СА-ВС |
||||||||
|
2и более |
Одиночные светильники: |
0,3 |
0,55/0,75 |
0,7/0,9 |
0,9/1,0 |
1,2 |
||
|
первый ряд |
0,45 |
0,5/0,65 |
0,65/0,75 |
0,8/0,9 |
1,2 |
|||
|
А-В-С-А-В-С |
0,6 |
0,5 |
0,65 |
0,75 |
1,1 |
|||
|
второй ряд |
0,75 |
0,45 |
0,6 |
0,7 |
0,85 |
|||
|
В-С- А- В-С-А |
0,9 |
0,4 |
0,5 |
0,65 |
0,8 |
|||
|
и т.д. |
1,2 |
0,4 |
0,45 |
0,6 |
0,7 |
|||
|
Сдвоенные светильники: |
0,3 |
0,6/0,5 |
0,9/0,7 |
1,2/1,0 |
1,2 |
|||
|
первый ряд |
0,45 |
0,6/0,5 |
0,85/0,7 |
1,2/1,0 |
1,2 |
|||
|
АВ-СА- ВС- АВ-СА- ВС |
0,6 |
0,6/0,5 |
0,85/0,7 |
1,2/1,0 |
1,2 |
|||
|
второй ряд |
0,9 |
0,6/0,5 |
0,8/0,7 |
1,1/1,0 |
1,2 |
|||
|
ВС-АВ-СА- ВС- АВ-СА |
1,2 |
0,6/0,5 |
0,7 |
1,0 |
1,2 |
|||
*А, В, С - фазы питающего напряжения..
Наибольшее из значений принимается за 100 %, а остальные два выражаются в долях от него. Соответственно полученным долям по табл. 1.11.6 для ОУ с ЛЛ и по табл. 1.11.7 для ОУ с ГЛВД определяется Кп.табл., которое представляет собой пульсацию освещенности в ОУ, если лампы имеют условный Кп.и. = 100%. Коэффициент пульсации в ОУ с источником света, имеющим реальную пульсацию светового истока Кп.и. ¹ 100 %, определяется по соотношению:
Кп = Кп.и. Кп.табл./100% (1.11.3)
Пример. Помещение освещается одноламповыми светильниками с ЛЛ типа ЛБ, включенными поочередно в три фазы (Кп.и. = 25 %). Определить Кп в расчетной точке ОУ, если лампы, включенные в разные фазы питающей сети, создают в этой точке соответственно освещенности 300, 120 и 60 лк.
Выражая освещенности в процентах от наибольшего значения (300), получаем: 100, 40 и 20%. По табл. 1.11.6 находим для источника света с Кп.и. = 100% значение Кп.табл. = 49,6 %. Коэффициент пульсации освещенности в ОУ с ЛЛ типа ЛБ находим по соотношению (1.11.2): Кп. = 25% ´ 49,6%100% = 12,4%.
Таблица 1.11.6
|
Значение Кп.табл. в ОУ с ЛЛ при освещенности от ламп второй фазы, % |
|||||||||||
|
100 |
90 |
80 |
70 |
60 |
50 |
40 |
30 |
20 |
10 |
0 |
|
|
0 |
42,3 |
45,0 |
48,0 |
51,2 |
54,5 |
59,9 |
64,9 |
71,5 |
79,3 |
88,5 |
100 |
|
10 |
37,4 |
39,4 |
41,8 |
44,9 |
47,8 |
52,3 |
56,9 |
62,6 |
69,0 |
77,1 |
- |
|
20 |
32,3 |
34,4 |
36,8 |
39,4 |
41,5 |
45,2 |
49,5 |
54,8 |
68,8 |
- |
- |
|
30 |
27,8 |
30,0 |
32,3 |
34,8 |
36,9 |
40,2 |
44,2 |
48,9 |
- |
- |
- |
|
40 |
23,4 |
25,9 |
27,9 |
30,2 |
32,6 |
35,4 |
39,2 |
- |
- |
- |
- |
|
50 |
19,8 |
23,2 |
24,2 |
26,3 |
28,5 |
31,4 |
- |
- |
- |
- |
- |
|
60 |
17,2 |
19,2 |
21,2 |
23,4 |
25,7 |
- |
- |
- |
- |
- |
- |
|
70 |
14,8 |
16,6 |
18,4 |
20,9 |
- |
- |
- |
- |
- |
- |
- |
|
80 |
12,4 |
14,2 |
16,3 |
- |
- |
- |
- |
- |
- |
- |
- |
|
90 |
10,4 |
12,3 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
100 |
8,9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Таблица 1.11.7
|
Значение Кп.табл. в ОУ с ГЛВД при освещенности от ламп второй фазы, % |
|||||||||||
|
100 |
90 |
80 |
70 |
60 |
50 |
40 |
30 |
20 |
10 |
0 |
|
|
0 |
49,9 |
50,3 |
50,9 |
52,4 |
53,9 |
56,5 |
61,0 |
67,1 |
74,2 |
88,5 |
100 |
|
10 |
40,0 |
40,5 |
41,0 |
41,5 |
43,0 |
46,0 |
51,0 |
56,0 |
62,5 |
69,9 |
- |
|
20 |
33,3 |
33,5 |
34,0 |
35,3 |
37,1 |
39,5 |
43,1 |
48,4 |
55,5 |
- |
- |
|
30 |
28,1 |
28,3 |
28,6 |
29,2 |
30,4 |
31,9 |
35,4 |
41,6 |
- |
- |
- |
|
40 |
22,8 |
23,0 |
23,5 |
24,5 |
26,0 |
28,1 |
31,0 |
- |
- |
- |
- |
|
50 |
18,0 |
18,4 |
19,4 |
20,5 |
22,4 |
24,5 |
- |
- |
- |
- |
- |
|
60 |
15,0 |
15,2 |
15,5 |
16,5 |
19,6 |
- |
- |
- |
- |
- |
- |
|
70 |
11,6 |
12,0 |
12,6 |
13,7 |
- |
- |
- |
- |
- |
- |
- |
|
80 |
9,3 |
9,7 |
10,6 |
- |
- |
- |
- |
- |
- |
- |
- |
|
90 |
8,8 |
9,0 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
100 |
7,9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Показатель дискомфорта
1.11.3. Проверка ОУ общественных зданий на соответствие регламентируемым значениям показателя дискомфорта М по МГСН 2.06-99 производится согласно табл. 1.11.8 и 1.11.9 в зависимости от светораспределения светильника (рис. 1.12) и распределения светового потока светильника в верхнюю и нижнюю полусферы, а также его геометрических размеров.
Определение соответствия OУ требованиям норм по М осуществляется в следующей последовательности.
По светораопределению светильника устанавливается группа светильника. По табл. 1.11.8 по доле светового потока, падающего в нижнюю полусферу, определяется подгруппа светильника. При этом коэффициент Км определяется по формуле:
![]() (11.1.4)
(11.1.4)
Таблица 1.11.8
|
ФÈ/Фсв |
Км |
Под группа |
Группа светильников и светораспределение |
|||
|
I |
II |
III |
IV |
|||
|
I = I0 cos a |
I = I0 cos1,43 a |
I = I0 cos2 a |
I = I0 cos3 a |
|||
|
0,76 - 1,00 |
1,1 |
а |
- |
- |
Л201Б420-01 |
- |
|
1,2 |
б |
Л201Б420-03, Л201Б420-18, Л201Б420-24 |
Л201Г220-22, Л201Б420-22, ЛПО13-2Х40/П-01, ЛВО13-2Х40/П-01, ЛПО02-4Х20/П-01, УСП-35-2Х20 |
- |
- |
|
|
1,3 |
в |
Л201Б420-04, Л201Б420-05, Л201Б440-22, Л201Г220-24, ЛП013-4+40/П-01, ЛВ013-4Х40Л1-01 |
Л201Б420-02 |
Л201Б440-01, УСП-35-4Х20 |
|
|
|
1,4 |
г |
Л201Б640-18, Л201Г220-23, Л201Г240-04М, Л201Г240-15М, УСП-11-4X20, ЛПО28-2Х40, ЛВО01-2Х40 |
Л201Б440-02, УСП-4-2Х20, УСП-4-4Х20, УСП-5-4Х20, УСП-9-4Х20, УСП-18-4X20 |
ЛВО01-4X40, УСП-35-6Х20, УСП-35-6Х20 |
- |
|
|
0,76 - 1,00 |
1,5 |
д |
Л201Г240-03М, Л201Б465-03М, Л201Б440-04М, Л201Г265-16М, ЛПО13-2Х65/П-01, ЛПО13-4Х65/П-01, ЛПО02-2Х20/П-01, ЛПО28-2Х65, ЛВО13-2Х65/П-01, ЛВО13-4Х65/П-01, УСП-4-6Х20, УСП-9-2Х20, УСП-11-2X20, УСП-11-6X20 |
Л201Г240-02М, УСП-5-6Х20, УСП-18-2X20, УСП-18-4Х20 |
- |
- |
|
0,76 - 1,00 |
1,2 |
е |
Л201Б440-03М, Л201Г265-15М, Л201Б440-15М, Л201Б640-15М, ЛВО01-1Х40, ЛВО03-2Х40-001, ЛВО03-2Х40-002, ЛВО03-2Х65-002 |
Л201Г265-01М, Л201Г265-02М |
Л201Б640-01, Л201Б440-01М, УСП-5-2Х40, ЛВО31-2Х80Б/П-03, ЛВО03-4Х40-001, ЛВО03-4Х40-002 |
- |
|
1,7 1,8 |
ж |
Л201Б440-03, Л201Б640-04, Л201Б440-04М, Л201Б440-05, Л201Г265-03М, Л201Б465-04М, Л201Б240-21, Л201Б440-21, Л201Б465-19М, Л201Б465-15М, |
Л201Б465-16М, Л201Б440-02М, Л201Б640-02М, УСП-4-2Х40 УСП-4-4Х40, УСП-4-6Х40 УСП-5-4Х40, УСП-5-6Х40 |
Л201Б640-01М, Л201Б465-01М, ЛПО02-4Х40/П-01, ЛПО02-4Х40/П-02, УСП-9-2Х40, УСП-9-4Х40, УСП-9-6Х40, УСП-11-4X40, УСП-11-6X40 УСП-35-2Х40, |
- |
|
|
0,76 - 1,00 |
|
|
Л201Г240-22, Л201Б420-23, УСП-11-2X40, УСП-18-2Х40, УСП-18-4X40, УСГМ8-6Х40, ЛПО02-2Х40/П-01 |
|
УСП-35-4Х40, УСП-35-6Х40, ЛВО03-4Х65-002 |
|
|
1,9 |
з |
Л201Б465-03М, ЛПО02-2Х40/П-02 |
Л201Б465-02М |
- |
- |
|
|
2,4 |
и |
- |
- |
- |
СВП 1X200 |
|
|
0,51 - 0,75 |
2,9 |
к |
- |
- |
- |
НВ-1Х100 |
|
3,3 |
л |
- |
- |
- |
СВП 1X100 |
|
|
3,6 |
м |
- |
- |
- |
СВП 1X500 |
|
|
1,2 |
н |
- |
- |
ШОД-2Х40, ШОД-2Х80, ЛСО02-2Х40/Р-01, ЛСО02-2Х40/Р-02, ЛСО02-2Х65/Р-01 |
- |
|
|
0,51 - 0,75 |
|
|
ЛСО02-2Х65/Р-С2 |
- |
ЛСО02-2Х65/Р-02, ЛСО02-4Х40/Р-02, ЛСО02-2Х40-003, ЛСО04-2Х40-004, ЛСО04-2Х65-003, ЛСО04-2Х65-004, ЛСО04-4Х40-003, ЛСО04-4Х40-004 |
- |
|
1,3 |
о |
- |
- |
ЛСО02-2Х40/Р-03, ЛСО04-2Х40-002, ЛСО04-2Х40-055 |
- |
|
|
1,4 |
п |
- |
- |
ЛСО02-2Х65/Р-03, ЛСО04-2Х65-002, ЛСО04-2Х65-005 |
- |
|
|
0,5 и менее |
0,9 1,1 |
р |
ПКР-300, СК-300 |
- |
- |
- |
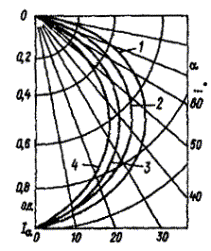
Рис. 1.12. Типовые кривые силы света светильников Ia
1 - I = I0 cos a;2 - I = I0 cos1,43 a; 3 - I = I0 cos2 a; 4 - I = I0 cos3 a
Рис. 1.13. Зависимость индекса помещения от его площади при различной расчетной высоте hp, м
1 - 1,8; 2 - 2,1; 3 - 2,7; 4 - 3,6; 5 - 4,5
где ФÈ - световой поток светильника в нижнюю полусферу, тыс. л, s - площадь выгодного отверстия светильника, м2 (подсчитывается по фактическим размерам светильника),
Согласно рис. 1.13 по площади и высоте помещения определяется индекс помещения in.
На табл. 1.11.9 согласно группе и подгруппе светильников, коэффициентам отражения стен rс и пола rп определяется значение индекса помещения in, при котором обеспечивается регламентируемое максимальное допустимое значение показателя дискомфорта М.
Оценка соответствия ОУ требованиям по ограничению слепящего действия по дискомфорту производится сравнением значений iT и in. При in < iT ОУ соответствует требованиям по дискомфорту; при in > iT - не соответствует.
Табл. 1.11.9 составлена для помещений с коэффициентом отражения потолка 0,5 и 0,7. Нормируемое значение показателя дискомфорта M = 90 обеспечивается при условиях, для которых составлена таблица. Нормируемое значение М, равное 60, обеспечивается при всех сочетаниях rс и rп кроме rс = 0,3 и rп = 0,1. Нормируемое значение М = 15 не обеспечивается при сочетаниях rс и rп, равных 0,3 и 0,1 (кроме подгруппы светильников 1 м, для которых iT = 1,1).
Таблица 1.11.9
|
Значение индекса помещения iT |
|||||||||||
|
Максимально допустимое значение М |
|||||||||||
|
15 |
25 |
40 |
60 |
||||||||
|
Рс |
0,5 |
0,5 |
0,5 |
0,5 |
0,3 |
0,3 |
0,5 |
0,5 |
0,3 |
0,3 |
0,3 |
|
Рп |
0,3 |
0,1 |
0,3 |
0,1 |
0,3 |
0,1 |
0,3 |
0,1 |
0,3 |
0,1 |
0,1 |
|
Iб |
- |
- |
2,2 |
1,5 |
1,1 |
1,0 |
+ |
+ |
4,2 |
2,4 |
+ |
|
Iв |
- |
- |
1,5 |
1,3 |
1,0 |
- |
+ |
+ |
2,6 |
2,1 |
+ |
|
Iг |
- |
- |
1,3 |
1,2 |
- |
- |
+ |
4,2 |
2,2 |
1,4 |
+ |
|
Iд |
- |
- |
1,2 |
1,1 |
- |
- |
+ |
3,1 |
1,4 |
1,3 |
+ |
Продолжение таблицы 1.11.9
|
Группа и подгруппа светильников |
Значение индекса помещения iT |
||||||||||
|
Максимально допустимое значение М |
|||||||||||
|
15 |
25 |
40 |
60 |
||||||||
|
Iе |
- |
- |
1,2 |
1,2 |
- |
- |
4,2 |
2,5 |
1,3 |
1,2 |
3,8 |
|
Iж |
- |
- |
1,1 |
1,0 |
- |
- |
2,6 |
2,2 |
1,2 |
1,1 |
2,5 |
|
Iз |
- |
- |
1,1 |
1,0 |
- |
- |
1,9 |
1,5 |
1,2 |
1,1 |
2,2 |
|
Iм |
1,6 |
1,4 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
IР |
1,4 |
1,1 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
IIб |
1,0 |
- |
+ |
2,4 |
1,2 |
1,1 |
+ |
+ |
+ |
+ |
+ |
|
IIв |
- |
- |
2,7 |
2,0 |
1,1 |
1,0 |
+ |
+ |
+ |
+ |
+ |
|
IIг |
- |
- |
2,1 |
1,4 |
1,0 |
- |
+ |
+ |
+ |
2,4 |
+ |
|
IIд |
- |
- |
1,4 |
1,2 |
- |
- |
+ |
+ |
+ |
1,5 |
+ |
|
IIе |
- |
- |
1,2 |
1,0 |
- |
- |
+ |
+ |
2,1 |
1,3 |
+ |
|
IIж |
- |
- |
1,1 |
1,0 |
- |
- |
+ |
3,5 |
1,4 |
1,2 |
+ |
|
IIз |
- |
- |
1,1 |
1,0 |
- |
- |
+ |
2,3 |
1,2 |
1,1 |
4,0 |
|
IIIa |
- |
- |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
IIIв |
- |
- |
+ |
+ |
+ |
1,1 |
+ |
+ |
+ |
+ |
+ |
|
IIIг |
- |
- |
+ |
+ |
1,1 |
- |
+ |
+ |
+ |
+ |
+ |
|
IIIe |
- |
- |
1,2 |
1,1 |
- |
- |
+ |
+ |
2,3 |
1,4 |
+ |
|
IIIж |
- |
- |
+ |
1,1 |
- |
- |
+ |
+ |
+ |
+ |
+ |
|
IIIн |
4,5 |
1,2 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
III |
1,2 |
1,0 |
4,0 |
2,4 |
1,3 |
1,1 |
+ |
+ |
+ |
3,9 |
+ |
|
IIIп |
1,0 |
- |
2,4 |
1,6 |
1,2 |
1,1 |
+ |
+ |
+ |
2,4 |
+ |
|
IVи |
- |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
+ |
|
IVк |
- |
- |
- |
- |
- |
- |
2,0 |
1,1 |
- |
- |
1,3 |
|
IVл |
- |
- |
- |
- |
- |
- |
+ |
+ |
+ |
- |
+ |
|
IVм |
- |
- |
- |
- |
- |
- |
+ |
- |
- |
- |
- |
Примечание. Знак «+» означает, что М не превышает регламентируемого значения при любых in; знак «-» - М превышает регламентируемое значение при любых in.
Пример. Для освещения конструкторского бюро размером 6 ´ 18 м, высотой 3 м коэффициенты отражения стен, потолка и пола которого, соответственно равны 0,5; 0,3 и 0,1, выбраны люминесцентные светильники типов Л201Б465-03М и ЛСО02-2х65/Р-01. Требуется оценить возможность использования указанных светильников для данной ОУ, исходя из требований к ограничению слепящего действия по дискомфорту. Регламентируемое значение М = 40.
По табл. 1.11.8 определяем группу и подгруппу светильников, соответственно, Iз и IIIн.
По табл. 1.11.9 определяем максимально допустимые значения индекса помещения in = 1,5 для светильников типа Л201Б465-03М, а для ЛСО02-2х65/Р-01. Значение М не превышает нормируемого значения при любых размерах помещения.
По рис. 1.13 определяем in = 2,05. Так как in > iT, то светильники типа Л201Б465-03М не обеспечивают регламентируемого значения М в данной ОУ.
Цилиндрическая освещенность
1.11.4. Цилиндрическая освещенность Ец есть средняя плотность светового потока на боковой поверхности вертикально расположенного цилиндра, размеры которого стремятся к нулю.
Цилиндрическая освещенность от отдельных светильников легко определяется делением вертикальной освещенности Ев в плоскости, перпендикулярной проекции луча на p:
Расчет цилиндрической освещенности производится инженерными методами. Значение Ец определяется на расстоянии 1 м от торцевой стены на центральной продольной оси помещения на высоте 1,5 м от пола.
В инженерном методе расчета для определения значения Ец принимаются следующие допущения.
1. Ограждающие поверхности помещения (пол, потолок, стены) принимаются диффузными, равнояркими по всей поверхности,
2. Светильники заменяются равнояркой поверхностью, каждый элемент которой имеет светораспределение, соответствующее светораспределению светильника.
3. Светораспределение светильника аппроксимилируется формулой:
I = I0 cosm a,
где I0 - сила света в направлении вертикали; Ia - сила света под углом a с вертикалью.
Значение m определяется по формуле
![]() ,
,
где ФÈ - световой поток светильника в нижнюю полусферу, равный для светильников прямого света 1000 лм.
Для расчета цилиндрической освещенности используются графики зависимости отношения средней горизонтальной освещенности к цилиндрической освещенности от индекса помещения, построенные для светильников с различным светораспределением.
Индекс помещения определен по высоте расположения светильников над расчетной плоскостью, на которой нормирована горизонтальная освещенность.
Кривые построены для различных сочетаний коэффициентов отражения стен и пола помещения.
Рис. 1.14. Графики для расчета цилиндрической освещенности
a) m = 1; б) m = 1,43; в) т = 2; г) т = 3
На всех графиках рис. 1.14. кривая I соответствует rст = 0,3, rр = 0,1; кривая 2 - rст = 0,3, rр = 0,3; кривая 3 - rст = 0,5; rр = 0,1; кривая 4 - rст = 0,5; rр = 0,3
Инженерный метод расчета справедлив при световых потоках в верхнюю полусферу менее 15 %, в других случаях применение этого метода может привести к значительным погрешностям.
Пример. В читальном зале размером 32 ´ 20 м, высотой 3,8 м на потолке установлены люминесцентные светильники прямого света, имеющие к.п.д. 70 % и силу света I0 = 270 кд. Коэффициенты отражения стен и пола соответственно равны 0,5 и 0,3.
Требуется определить, на какую горизонтальную освещенность должно быть рассчитано освещение помещения, чтобы получить цилиндрическую освещенность 150 лк. Для данного светильника
![]() = 6,28 - 270/700 - 1 » 1,4.
= 6,28 - 270/700 - 1 » 1,4.
Индекс помещения in = 640/(3,8(32+20)) = 3,2. На рис. 1.14 находим ЕГ/Ец = 2,52, откуда ЕГ = 2,52×150 = 378 лк. Коэффициент запаса учтен при составлении графиков.
2. ИСКУССТВЕННОЕ ОСВЕЩЕНИЕ ПОМЕЩЕНИЙ ОБЩЕСТВЕННЫХ ЗДАНИЙ
2.1. Общие положения
2.1.1. Основные требования к ОУ помещений общественных зданий должны определяться исходя из нормированных показателей освещения и функционального назначения помещения.
Конкретные приемы освещения помещений должны выбираться совместно светотехником и архитектором.
2.1.2. Совместная работа архитектора и светотехника должна осуществляться в следующей последовательности:
в соответствии с общим архитектурным замыслом выбираются система освещения и тип источников света, ориентировочно определяется мощность ламп и рассматривается ряд возможных для использования типов светильников и вариантов их размещения (применение нестандартных специальных светильников возможно только в исключительных случаях для уникальных объектов или при отсутствии подходящих стандартных светильников);
производится окончательный выбор типа, светильников и их размещение.
2.1.3. Технико-экономические сопоставления проводятся при необходимости выбора одного из вариантов ОУ и могут служить основанием для принятия решения только при равных осветительных условиях, обеспечивающих одинаковую работоспособность в основных рабочих помещениях и равных условиях восприятия интерьеров в помещениях с повышенными требованиями к архитектурно-художественному оформлению интерьера.
2.1.4. Для освещения помещений общественных зданий предусматривается рабочее, аварийное, эвакуационное и дежурное освещение.
2.1.5. Аварийное освещение следует предусматривать в помещениях диспетчерских, операторских, киноаппаратных, узлов связи, электрощитовых, здравпунктов, аккумуляторных, дежурных пожарных постов, на постах постоянной охраны, в гардеробах с числом мест хранения 300 и более, а также в главных кассах, в детских комнатах и дебаркадерах крупных магазинов, в помещениях торговых залов магазинов самообслуживания, в вестибюлях гостиниц, залах ресторанов и помещениях спасательного фонда гостиниц.
В помещениях насосных, тепловых пунктов и бойлерных аварийное освещение предусматривается только при постоянном пребывании дежурного персонала или если токоприемники данных помещений относятся к нагрузкам I категории надежности электроснабжения.
2.1.6. Эвакуационное освещение предусматривается в проходах и на лестницах, предназначенных для эвакуации людей из зданий, где пребывает одновременно свыше 50 человек, а также из здравпунктов, книго- и архивохранилищ, независимо от числа лиц, пребывающих там; в плавательных бассейнах, спортивных и актовых залах, рекреациях, гардеробных, проходных помещениях, коридорах и на лестницах общеобразовательных школ, профтехучилищ и средних специальных учебных заведений; в групповых, игральных, столовых, приемных, раздевальных, коридорах и на лестничных клетках, а также в кухнях и стирально-разборочных помещениях детских дошкольных учреждений; в ожидальных, раздевальных, мыльных, душевых помещениях бассейнов и парильных бань; в помещениях, где одновременно могут находиться свыше 100 чел. (большие аудитории, обеденные залы, актовые залы и т.п.); в торговых залах и на путях выхода из них, в магазинах с торговыми залами общей площадью 90 м2 и более, в транспортных туннелях торговых предприятий; в помещениях с постоянно работающими в них людьми, если вследствие отключения рабочего освещения и продолжения при этом работы производственного оборудования может возникнуть опасность травматизма (производственные помещения предприятий общественного питания, бытового обслуживания населения и т.п.).
2.1.7. Световые указатели «Выход» должны быть установлены у выходов из помещений обеденных и актовых залов, больших аудиторий, конференц-залов и других помещений, рассчитанных на одновременное пребывание свыше 100 чел., а также коридоров, к которым примыкают помещения, где могут одновременно находиться свыше 50 чел., у выходов из торговых залов общей площадью 180 м2 и более, во всех магазинах и из торговых залов общей площадью 110 м2 и более.
2.1.8. В помещениях общественных зданий, как правило, следует применять систему общего освещения.
Допускается применение системы комбинированного освещения в помещениях общественных зданий, где выполняется зрительная работа разрядов А-В по СНиП 23-05-95 (например, кабинеты, рабочие комнаты, читальные залы библиотек и архивов и т.п.) В производственных помещениях общественных зданий (ремонт одежды, часов, телевизоров, радиоаппаратуры и т.д.) следует применять систему комбинированного освещения (общее + местное).
2.1.9. Для повышения энергоэффективности осветительных установок следует, как правило, предусматривать в проектах разрядные источники света.
Световая отдача разрядных источников света для общего искусственного освещения помещений общественных зданий при минимально допустимых индексах цветопередачи не должна быть меньше значений, приведенных в табл. 2.1.1.
Таблица 2.1.1
|
Световая отдача, лм/Вт, не менее при минимально допустимых индексах цветопередачи |
||||
|
Rа > 80 |
Rа > 60 |
Rа > 45 |
Ra > 25 |
|
|
Люминесцентные лампы |
50 |
75 |
|
|
|
Компактные люминесцентные лампы |
70 |
|
|
|
|
Металлогалогенные лампы |
|
75 |
|
|
|
Дуговые ртутные лампы |
|
|
50 |
|
|
Натриевые лампы высокого давления |
|
75 |
|
85 |
Основные цветовые и энергетические характеристики разрядных источников света приведены в табл. 2.1.2.
Таблица 2.1.2
|
Световая отдача, лм/Вт |
Индекс цветопередачи, Rа, не менее |
Цветовая температура, Тцб, К |
||||
|
Люминесцентные лампы* |
||||||
|
ЛБ |
80 |
57 |
3500 |
|||
|
ЛБЦТ |
75 |
83 |
4000 |
|||
|
ЛХБ |
75 |
62 |
4300 |
|||
|
ЛДЦ |
55 |
92 |
6000 |
|||
|
ЛЕЦ |
54 |
85 |
3900 |
|||
|
ЛХЕ |
48 |
92 |
5200 |
|||
|
ЛДЦУФ |
40 |
92 |
6000 |
|||
|
Компактные люминесцентные лампы |
||||||
|
КЛТБЦ |
65 - 80** |
85 |
2800 |
|||
|
Разрядные лампы высокого давления |
||||||
|
ДРИ |
66 - 99** |
65 |
4700 - 6500 |
|||
|
ДнаТ |
85 - 120** |
25 |
2100 |
|||
|
ДРЛ (10 - 15)*** |
50 - 54** |
40 |
3800 |
|||
|
Лампы накаливания |
||||||
|
Общего назначения |
15,3 |
100 |
2800 |
|||
|
Галогенные |
22,0 |
100 |
2800 |
|||
* - данные приведены для мощности 40 Вт,
** - данные приведены в зависимости от мощности,
*** - красное соотношение.
2.1.10. Общее освещение помещений разрядов А-В (СНиП 23-05-95) следует выполнять преимущественно люминесцентными лампами, в том числе компактными.
Разрядные лампы высокого давления типов ДРИ, ДНаТ, ДРЛ с улучшенной цветопередачей рекомендуется применять для освещения:
- помещений с осветительными установками отраженного света,
- помещений высотой более 7 м,
- помещений, в осветительных установках которых используются полые цилиндрические и плоские световоды,
- производственных помещений, приравненных к промышленным (например, цехов, прачечных).
2.1.11. Общее освещение помещений разрядов Г-Е (СНиП 23-05-95) при невысоких требованиях к цветопередаче допускается выполнять лампами типов ДРИ, ДНаТ, а также ДРИ совместно с ДНаТ в специально разработанных для них светильниках.
2.1.12. Общее освещение вспомогательных помещений разрядов Д-Ж (СНиП 23-05-95) (вестибюлей, фойе, парадных лестниц) рекомендуется выполнять люминесцентными лампами, в том числе компактными и лампами типов ДРИ, ДНаТ и ДРЛ с улучшенной цветопередачей.
2.1.13. Местное освещение помещений административных зданий (кабинетов, рабочих комнат, читальных залов библиотек и т.п.) следует выполнять люминесцентными лампами, в т.ч. компактными. Допускается использование в светильниках местного освещения ламп накаливания, в т.ч. галогенных.
2.1.14. Лампы накаливания следует применять для общего освещения:
- помещений, где по технологическим требованиям недопустимо применение разрядных ламп (например, в помещениях для работы с материалами, которые под воздействием излучения разрядных ламп теряют свои свойства, и в помещениях, где радиопомехи, создаваемые светильниками с разрядными лампами, недопустимы для работы технологического оборудования) - киноаппаратные, помещения для звукозаписи,
- помещений, где для оформления интерьера требуется применение ламп накаливания (залы ресторанов, кафе, баров, фойе и т.п.),
- спальных и веранд используемых только в летнее время,
- вспомогательных помещений - кладовых, машинных отделений лифтов, электрощитовых, техподполий,
- моечных, душевых и парильных в банях,
- охлаждаемых помещений и холодильных камер.
Основные цветовые и энергетические характеристики ламп накаливания приведены в табл. 2.1.2.
2.1.15. Общее освещение помещений общественных зданий при отсутствии специальных требований к цветопередаче и комфортности следует выполнять люминесцентными лампами типа ЛБ.
Общее освещение помещений, где производится:
- сопоставление цветов с высокими требованиями к цветоразличению и выбор цвета (например, специализированные магазины «Ткани», «Одежда») следует выполнять люминесцентными лампами типов ЛДЦ, ЛХЕ,
- сопоставление цветов с высокими требованиями к цветоразличению (например, выставочные и демонстрационные залы, кабинеты рисования, парикмахерские и т.д.) следует выполнять люминесцентными лампами типов ЛБЦТ, ЛЕЦ, ЛХЕ,
- различение цветных объектов при невысоких требованиях к цветоразличению (например, универсамы, ателье химической чистки одежды и т.д.) следует выполнять люминесцентными лампами типов ЛБ, ЛТБЦТ, КЛЛ.
2.1.16. Выбор типов светильников общего освещения следует проводить с учетом их светотехнических параметров, внешнего вида, экономической эффективности и условий окружающей среды. Характеристика помещений по условиям окружающей среды дана в табл. 2.1.3, рекомендации по выбору исполнения светильников в зависимости от характеристики помещений по условиям среды приведены в табл. 2.1.4.
Во взрывоопасных и пожароопасных зонах следует применять светильники, удовлетворяющие требованиям раздела 6 ПУЭ.
Таблица 2.1.3
|
Наименование помещений и зон |
|
|
Пожароопасные: |
|
|
класса П-I |
Закрытые автостоянки, расположенные под зданиями Столярные мастерские |
|
класса П- II |
Фонды открытого доступа к книгам, книгохранилища |
|
класса П-IIа |
Архивы, переплетные и макетные мастерские, печатные отделения офсетной печати, светокопировальные, киноаппаратные, перемоточные, помещения для нарезки тканей, рекламно-декарационные мастерские, витрины с экспозицией из горючих материалов, помещения для хранения бланков, упаковочных материалов и контейнеров, отделения приема и выдачи белья и одежды, отделения разборки, починки и упаковки белья, пошивочные цехи, закройные отделения, отделения подготовки прикладных материалов, помещения ремонта одежды, ручной и машинной вязки, изготовления и ремонта головных уборов, скорняжных работ, фонотек, кладовые продуктов в сгораемой упаковке, кладовые в непродовольственных магазинах, кладовые пункты проката и спецодежды, чердаки, кладовые и подсобные помещения квартир и домов усадебного типа |
|
Пыльные |
Отделы электрофотографирования |
|
Влажные |
Фотолаборатории, дистилляторные, автоклавные, горячие, доготовочные и заготовочные цехи, загрузочные, кладовые и моечные тары, кладовые овощей, раздевальные в банях, душевые, сушильно-гладильные отделения, прачечные с самообслуживанием, утюжные, декатировочные, санитарные узлы, тепловые пункты, охлаждаемые камеры |
|
Сырые |
Моечные кухонной и столовой посуды, отделения механической стирки, приготовления стиральных растворов, насосные, бассейны |
|
Особо сырые |
Отделения ручной стирки, душевые, моечные, парильные |
|
Жаркие |
Горячие цехи предприятий общественного питания, парильные, моечные |
|
Химически активные |
Отделения химической чистки |
Примечание. В каждом конкретном случае характеристика помещения (зоны) по условиям среды уточняется в проекте. Характеристика помещений, не указанных в таблице, также определяется в проекте здания.
Таблица 2.1.4
|
Степень защиты светильников по ГОСТ 14254-80 ГОСТ 17677-82 |
Тип источника |
Характеристика помещений по условиям среды |
||||||
|
нормальные |
влажные |
сырые |
особо сырые |
с химически активной средой1,4 |
пыльные7 |
жаркие |
||
|
IP20 |
ЛЛ |
+ |
x |
- |
- |
- |
х8 |
+10 |
|
|
ЛН, ГЛВД |
+ |
х |
х2 |
- |
- |
х8 |
+ |
|
IP23 |
ЛЛ, ЛН, ГЛВД |
(-) |
+ |
х3 |
х3 |
х3,12 |
х8 |
х |
|
2¢0 |
ЛЛ |
+ |
x |
(-) |
- |
- |
- |
х10 |
|
|
ЛН, ГЛВД |
+ |
x |
(-) |
- |
- |
- |
х11 |
|
5¢0 |
ЛН, ГЛВД |
(-) |
(-) |
x2 |
- |
x |
+9,13 |
+ |
|
5¢3 |
ЛН, ГЛВД |
(-) |
(-) |
х3 |
х3 |
х3 |
+9,13 |
x |
|
IP51 |
ЛН |
(-) |
(-) |
+6 |
+6 |
х6 |
+ |
x11 |
|
5¢4 |
ЛЛ |
(-) |
(-) |
+ |
+ |
+ |
+ |
+10 |
|
IP53 |
ЛН, ГЛВД |
(-) |
(-) |
+3 |
+3 |
+3 |
+ |
х11 |
|
IP54 |
ЛЛ |
(-) |
(-) |
+ |
+ |
+ |
+ |
х10 |
|
|
ЛН |
(-) |
(-) |
+ |
+ |
+5 |
+ |
х11 |
|
|
ГЛВД |
(-) |
(-) |
+ |
+ |
+ |
+ |
x |
Условные обозначения: + - светильники рекомендуются; х - допускаются; -запрещаются; (-) - применение светильников возможно, но нецелесообразно.
1 Предпочтительны светильники с корпусами и отражателями из влагостойкой пластмассы, фарфора, покрытые силикатной эмалью.
2 Допускается при отсутствии капель воды, падающих на светильники при наличии фарфорового патрона.
3 При наличии брызг воды (растворов), падающих на светильник под углом более 60° к вертикали установка светильников со степенями защиты IP23 и 5¢3 с JIH и ГЛВД запрещается.
4 Рекомендуются светильники, специально предназначенные для химически активной среды.
5 Светильники, которые могут сверху заливаться водой или раствором, должны иметь боковой ввод проводов.
6 При наличии брызг воды (растворов), падающих на светильник под углом более 15° к вертикали, светильники с нетермостойким стеклом допускаются при условии установки в них ламп меньшей мощности, чем номинальная для данного светильника.
7 В пыльных помещениях рекомендуется применение в светильниках ламп с внутренним отражающим слоем и не рекомендуется применение светильников с экранирующими решетками, сетками и подобными элементами, способствующими запылению.
8 Светильники допускаются при ограниченном количестве пыли в зоне их установки.
9 Светильники со степенью защиты 5¢Х (например, 5¢3) предпочтительнее светильников со степенью защиты IP5X (например, IP53), в частности в следующих случаях: количество пыли мало, пыль светлая, светильники располагаются в местах, неудобных для обслуживания, помещение жаркое.
10 В светильниках рекомендуется устанавливать амальгамные люминесцентные лампы типа ЛБА.
11 Рекомендуется установка в светильниках с лампами накаливания указанных степеней защиты ламп меньшей мощности, чем номинальная для данного светильника.
12 Допускаются при условии выполнения деталей светильников, контактов патронов и цоколей ламп из материала, не подверженного коррозии в данной химически активной среды.
13 Преимущественно с лампами-светильниками или рефлекторными ЛЛ.
2.1.17. В помещениях общественных зданий следует отдавать предпочтение светильникам с коэффициентом полезного действия не менее 55%.
2.1.18. В рабочих помещениях целесообразно использовать светильники преимущественно прямого и рассеянного света с кривой силы света типа Л в нижней полусфере.
2.1.19. В помещениях со светлыми потолками административных и учебных зданий для уменьшения контрастов яркости в поле зрения должны применяться, как правило, светильники, направляющие в верхнюю полусферу не менее 10 - 15% излучаемого ими светового потока.
2.1.20. Для создания наибольшего уровня вертикальной освещенности в осветительной установке общего равномерного освещения следует применять светильники с кривыми силы света типов Л, Д и М.
2.1.21. При устройстве акцентирующего освещения следует использовать светильники со значительной концентрацией светового потока с кривыми силы света К и Г.
2.1.22. Для создания мягкого, бестеневого и неслепящего освещения следует применять настенные или напольные светильники отраженного света с галогенными лампами накаливания мощностью до 300 Вт и металлогалогенными лампами мощностью 70, 150, 250 Вт с несимметричными зеркальными отражателями.
2.1.23. Для создания в помещении высокой равномерности освещения, а также при необходимости варьирования спектра излучения рекомендуется использование полых цилиндрических и плоских световодов.
2.1.24. Освещение рабочих поверхностей, обладающих направленным, направленно-рассеянным или смешанным отражением, должно предусматриваться с учетом мер по ограничению отраженной блескости согласно СНиП 23-05-95.
2.1.25. Для соблюдения нормируемых СНиП 23-05-95 и МГСН 2.06-99 значений коэффициентов пульсации в рабочих помещениях следует применять многоламповые светильники с ПРА, состоящих из равного числа опережающих и отстающих ветвей и равного числа ламп. Предпочтительно использование светильников с электронными ПРА.
2.1.26. При устройстве комбинированного освещения в помещениях административных зданий, где выполняется зрительная работа А-В разрядов по СНиП 23-05-95, светильники местного освещения должны удовлетворять требованиям ГОСТ 8607. Отдавать предпочтение следует светильникам с компактными люминесцентными лампами и галогенными лампами накаливания.
2.1.27. В учебных классах, спортивных и актовых залах учебных заведений, помещений детских дошкольных учреждений, в конструкторских бюро следует предусматривать либо отключение светильников рядами, параллельными световым проемам, либо плавное или ступенчатое регулирование в зависимости от естественного освещения.
2.1.28. Освещение лестниц, холлов, коридоров должно иметь автоматическое или дистанционное управление, обеспечивающее отключение части светильников или ламп в ночное время с таким расчетом, чтобы освещенность в этих помещениях была не ниже норм эвакуационного освещения.
2.1.29. Для уменьшения контрастов яркости в поле зрения коэффициенты отражения ограждающих поверхностей и мебели должны иметь следующие значения: потолка 0,7 - 0,75; стен 0,4 - 0,5; пола 0,3, мебели 0,4.
2.1.30. Светильники отраженного света по условиям ограничения слепящего действия являются наилучшими, так как полностью исключают блескость и не создают теней. Эксплуатация установок отраженного освещения значительно дороже и сложнее, чем установок прямого и рассеянного света. Потребляемая мощность при отраженном освещении возрастает в два-три раза по сравнению с мощностью прямого освещения.
2.1.31. Локализованное размещение светильников применяется в торговых залах магазинов, книгохранилищах, архивах, выставочных помещениях с постоянно фиксированными плоскостями экспозиции и т.п.
2.1.32. Для основных помещений общественных зданий размещение светильников прежде всего определяется отношением расстояния между светильниками к высоте подвеса l = lсв/ hcв. Уменьшение этой величины удорожает устройство и обслуживание освещения и часто приводит к применению ламп с пониженной световой отдачей, а чрезмерное увеличение ведет к резкой неравномерности освещенности и возрастанию расхода электроэнергии.
В табл. 2.1.5 приведены рекомендуемые значения l для светильников с типовыми кривыми силы света (КСС).
Таблица 2.1.5
|
lс |
lэ |
|
|
Косинусная |
1,4 |
1,6 |
|
Полуширокая |
1,6 |
1,8 |
|
Равномерная |
2,0 |
2,6 |
Если увеличение расстояния между светильниками не сопровождается повышением единичной мощности и световой отдачи ламп, следует руководствоваться значениями lс (светотехнически наивыгоднейшее расположение), а в остальных случаях - lэ (энергетически наивыгоднейшее расположение).
При размещении светильников общего освещения для сохранения равномерности распределения освещенности по помещению расстояние от крайнего ряда светильников до стен не должно превышать 0,25 - 0,3 расстояния между рядами светильников.
2.1.33. В помещениях с повышенными требованиями к оформлению интерьера размещение светильников должно быть увязано с архитектурным ритмом, который определяется оконными проемами, простенками между ними, колоннами, кессонами и т.п. Размещение осветительных приборов должно подчеркивать этот ритм, т.е. они должны размещаться, например, между колоннами, простенками и т.д.
2.1.34. Архитектурно-художественное освещение помещений может быть выполнено:
светильниками (встраиваемыми, потолочными, подвесными, настенными и напольными);
светящими потолками и панелями (рис. 2.1).
2.1.35. При освещении архитектурных элементов интерьера следует учитывать, что в зависимости от способа освещения архитектурная форма воспринимается совершенно различно. Например, плоская поверхность (потолок, пол) только тогда воспринимается плоской, когда она освещается равномерно. Уменьшение яркости в центре потолка создает впечатление его провисания, а потолок, имеющий повышенную яркость в центре, воспринимается в виде свода.
Рис. 2.1. Основные светотехнические схемы светящих потолков
1 - отражающая поверхность; 2 - рассеивающая светопропускающая поверхность; а - рассеивающие светящие потолки; б - отражающие светящие потолки
Усилением яркости в центре можно придать куполу кажущуюся большую кривизну, создать иллюзию повышения высоты помещения. Увеличение яркости по периметру, наоборот, вызовет ощущение понижения купола (обычно результат неправильного устройства световых карнизов).
Вертикально вогнутые членения (каннелюры, ниши и др.) также не должны освещаться равномерно. Односторонние мягкие тени способствуют правильному восприятию их формы. Так при системе отраженного освещения пилястры почти незаметны и дорогостоящая отделочная работа оказывается бесполезной. При использовании в том же помещении редко расположенных подвесных светильников создаются односторонние тени, блики, что хорошо выявляет раскреповку пилястр, и способствует восприятию их формы и фактуры. Освещение системы крупных кессонов решается удовлетворительно, когда число светильников принимается равным числу кессонов. Размещение светильников через два-три кессона (в случае мелких кессонов) приводит к образованию в промежуточных кессонах неприятных теней. В этом случае наилучший результат может быть достигнут при освещении кессонированного потолка напольными светильниками, установленными в соответствии с модулем кессонов. Для освещения настенного декора (фризов, лепки) рекомендуется создавать неравномерное распределение яркости, снижающееся сверху вниз, поэтому при наличии декоративных поясов в верхней части стен светильники следует располагать непосредственно у потолков или применять систему отраженного освещения. Однако необходимо учитывать, что при мелком рельефе лепной отделки отраженное освещение ухудшает восприятие лепки. Особые требования предъявляются к помещениям, в которых располагается скульптура: для правильного выявления формы и фактуры скульптурных произведений освещение должно создавать мягкие односторонние тени, направленные под некоторым углом сверху вниз.
2.1.36. При использовании светильников художественный эффект может быть достигнут соответствующим их расположением в композиционные схемы и применением в одном помещении различных осветительных приборов.
2.1.37. Используемые в практике освещения светящие поверхности равномерной яркости могут быть выполнены в виде установок отраженного света (рис. 2.2) или светящих панелей. Основные требования, предъявляемые к ним, заключаются в обеспечении заданной освещенности в расчетной плоскости, равномерном распределении яркости по светящей поверхности и в поле зрения. Соблюдение этих требований определяется размещением светящих поверхностей в поле зрения, а также расположением источников света или светильников относительно отражающей поверхности в установках отраженного света или относительно рассеивателя в светящих панелях.
2.1.38. В ОУ отраженного света со световыми карнизами основными отражающими поверхностями являются потолок и часть стен, расположенная выше карниза. Основное требование к таким установкам заключается в обеспечении равномерного распределения яркости вдоль светящего карниза, значительно меньшие требования предъявляются к распределению яркости в плоскости, перпендикулярной к светящему карнизу. Источники света и отражатели светильников, расположенные в карнизе, должны быть полностью экранированы от поля зрения наблюдателя, находящегося в освещаемом помещении. Установки отраженного света могут быть выполнены не только в виде светящего потолка, но и в виде отдельных светящих ниш, расположенных в плоскости потолка или стен. В первом случае световые карнизы с осветительными средствами размещаются вдоль всех четырех стен помещения или вдоль двух продольных стен на определенном расстоянии от потолка.
Значение КПД ОУ отраженного света зависит от значений коэффициентов отражения карниза, потолка и стен помещения, расположенных выше карниза, а также формы карниза (карниз должен быть достаточно широким и по возможности неглубоким). При этом лампы и другое оборудование карниза следует располагать ниже визирной линии (рис. 2.3), проведенной через верхний край козырька карниза и глаза человека, расположенного на наибольшем удалении от карниза. Кроме того, козырек карниза не должен экранировать прямых лучей, падающих на потолок от лампы или светильника, т.е. не должен быть выше створной линии, соединяющей нижнюю точку светящего элемента лампы или светильника (трубки люминесцентной лампы, нити лампы накаливания) с противоположным краем потолка или при наличии двухсторонних карнизов - с продольной осевой линией потолка.
Рис. 2.2. Способы устройства отраженного освещения
а - напольные светильники отраженного света; б - «парящий» потолок; в - накладной и вырезанный потолки; г - ступенчатый потолок: д - падуги
Рис. 2.3. Световой карниз
1 - створная линия; 2 - визирная линия; 3 - дополнительный створ
Рис. 2.4. Расположение зеркальной вставки
1 - зеркало; 2 - направление к четверти ширины потолка; 3 - направление на удаленный край или центр потолка
Равномерность распределения яркости по отражающей поверхности зависит от типа источника света (светильника) и их размещения в световом карнизе, ширины помещения bп высоты размещения потолка над световыми карнизами (над световым центром лампы) hк, от типа светового карниза (одно-двухсторонний, замкнутый), расстояния центра ближайшей лампы до стены а, расстояния между световыми центрами соседних ламп lл, расстояния между рядами люминесцентных ламп (между осями ламп) с, максимального расстояния карниза от стены f, расстояния между люминесцентными лампами lлл (рис. 2.3, 2.5). Люминесцентные лампы обычно монтируются на панелях, на которых размещаются ПРА, патроны и стартеродержатели. Отражателями являются панель, поверхность карниза, стена и потолок. Требуемая равномерность распределения яркости обеспечивается при bn/hk £ 5 при двухстороннем и bn/hk £ 2 - при одностороннем карнизе. Эти условия трудно осуществимы, поэтому для увеличения соотношений используют плоские зеркальные вставки, которые позволяют увеличить значение bn/hk соответственно до 7 и 3. Расположение и размер зеркальной вставки определяются согласно рис. 2.4. Створная линия составляет угол a с горизонталью, проведенной через центр лампы. Края зеркальной вставки определяются построением, указанным на рис. 2.4, на котором углы a и b образуются пересечением касательной к лампе с основанием карниза. При этом минимальная ширина зеркала определяется параллельными прямыми АВ и CD, максимальная СЕ - углом b. Увеличение размера зеркальной вставки до СЕ означает, что сила света будет усилена в пределах большего угла. При этом зеркальная вставка не должна быть видна из любых точек наблюдения в помещении. Так, лучшие результаты достигаются при использовании криволинейных зеркал или зеркальных ламп. Значительно проще создать требуемое распределение яркости при наличии сферических или цилиндрических сводов. При таких условиях удовлетворительное распределение яркости наблюдается при любых значениях hk. Достаточная равномерность распределения яркости при этом обеспечивается при hk/a £ 3,5. Даже при увеличении этого соотношения распределение яркости может считаться допустимым, однако в этом случае коэффициент использования резко снизится. Практика показала, что значения расстояния от лампы до стены (а) при однорядном расположении ламп должно находиться в пределах 120 - 150 мм, при многорядном - составлять не менее 75 мм. Чтобы избежать при многорядном расположении ламп возможного снижения яркости стены напротив разрыва между лампами используется сдвиг рядов ламп на 80 - 100 мм по длине карниза (рис. 2.5).
Зеркальные лампы концентрированного светораспределения нашли применение при карнизном освещении. Они позволяют создавать равномерное распределение яркости по поверхности потолка освещаемого помещения ближе к его центру, что особенно важно для широких помещений. Недостатком применения таких ламп является наличие ярких пятен, создаваемых на потолке вблизи карниза, для исключения которых необходимо располагать карниз возможно дальше от потолка (hk ³ 1,5 м). Для сокращения ширины карниза f лампы следует устанавливать возможно ближе к стене. Ось лампы должна быть направлена на противоположный край потолка как при одностороннем, так и при двухстороннем расположении карнизов (рис. 2.6); соотношение bn/hk, при зеркальных лампах и двухстороннем расположении карниза увеличивается до 7,5. Зеркальные лампы устанавливаются со значительными разрывами, достигающими 2 м, поэтому чаще всего при их использовании применяется одиночная установка патронов на скобах, обеспечивающих регулирование угла наклона лампы.
Рис. 2.5. Двухрядное размещение люминесцентных ламп в карнизе
Рис. 2.6. Использование зеркальных ламп в снеговых карнизах
Лампы накаливания общего назначения также используются в карнизах. Требования по применению ЛЛ справедливы и для ЛН. Расстояние от стены а желательно по возможности увеличивать, минимальное значение а = 150 мм. Применение ЛН в матированной колбе незначительно повышает равномерность распределения яркости. Максимальное отношение l/hк не должно превышать 1,5. При горизонтальном расположении ламп в карнизе l/hк допускается увеличивать до 2 при лампах в прозрачной колбе. Минимальная мощность ламп, применяемых в карнизе 40 - 60 Вт.
Коэффициент использования ОУ карнизного освещения Ко.у.к. при расчете освещенности на полу или на любой горизонтальной поверхности определяется по формуле:
Ко.у.к. = hк Кп.р., (2.1.1)
где Ко.у.к. - коэффициент использования установки карнизного освещения; Кп.р. - коэффициент использования светового потока карниза, hк - КПД карниза.
КПД карниза с JIH или с ЛЛ определяется с учетом формы свода по формуле
![]() , (2.1.2)
, (2.1.2)
где x - доля светового потока источников, падающая на отражающую поверхность карниза, равная отношению значения двухгранного угла в градусах, в пределах которого поток падает на эту поверхность, к 360°; r - коэффициент отражения поверхности карниза; Асв - площадь выходного отверстия карниза; Аотр - площадь отражающей поверхности карниза.
Практика расчета и эксплуатации карнизов показала, что КПД карнизов имеет значение, близкое к 60 %. Значение r рекомендуется принимать равным 0,5, учитывая в карнизах наличие проводов и плохо отражающих конструктивных частей. При карнизном освещении коэффициент z, характеризующий неравномерность освещения, не учитывается, так как этот вид освещения создает достаточно высокую равномерность и рассчитывается по средней освещенности.
2.1.39. В настоящее время нашли применение световые потолки рассеянного света, через которые в светлое время суток осуществляется естественное освещение помещения, а в вечернее и ночное - искусственное от светильников, расположенных в полости фонарей. Часто встречаются световые потолки только искусственного света, выполненные светильниками с люминесцентными лампами или только одними лампами, расположенными за плоскостью светового потолка.
2.1.40. Световые потолки могут выполняться в виде сплошной поверхности или световых полос. Для светящих потолков используются источники света, установленные в коробе, перекрытом рассеивателем (молочным органическим стеклом), или светильники, расположенные в технической полости над рассеивателем такого же типа.
При ширине светящей панели, превышающей 2 м, и достаточной высоте над рассеивателем целесообразно использовать светильники, так как это увеличивает КПД светового устройства. Основное требование к светящим потолкам заключается в равномерном распределении яркости по светящей поверхности. Предельно допустимым значением яркости для светящего потолка следует считать 2000 кд/м2 в высоких и 1000 кд/м2 - в низких помещениях (при высоте менее 6 м). Чем равномернее распределение яркости по светящему потолку, тем благоприятнее он воспринимается глазом.
При наличии над световым потолком высокой технической полости применяются светильники прямого света с ЛЛ, реже с ЛН, подвешиваемые над светящей поверхностью. Расположение светильников или рядов светильников должно быть таким, чтобы обеспечивалось равномерное распределение яркости по светящему потолку. Для выполнения этого условия наибольшее относительное расстояние между соседними излучателями или их сплошными рядами не должно превышать значений, указанных в табл. 2.1.6.
При подвесных потолках лампы обычно устанавливаются без отражателей, роль отражателя играет побеленная поверхность несущего перекрытия. Такое устройство удобно применять с ЛЛ. Для светящего потолка или светящих полос следует использовать светильники-блоки прямого света с открытыми ЛЛ, например, серии ЛПО09. Светильники с ЛЛ следует устанавливать сплошными рядами над рассеивающим стеклом панели. На чердаке светильники могут крепиться непосредственно к кровле, подвешиваться на тросах или устанавливаться на металлических стойках, используемых для натяжки проводов электрической сети.
Таблица 2.1.6
|
Тип кривой силы света излучателя |
Значения отношения lСВ/hCB |
||
|
рекомендуемое |
допустимое |
||
|
Точечный |
Глубокая |
0,7 |
0,9 |
|
Точечный |
Косинусная |
1,0 |
1,5 |
|
Точечный |
Равномерная |
1,2 |
1,8 |
|
Линейный |
Косинусная |
1,2 |
1,8 |
|
Линейный |
Равномерная |
1,4 |
2,4 |
2.1.41. Для обслуживания ОУ на чердаках, над остеклением устраиваются переходные мостики, по которым можно подойти к светильнику. Мостики, расположенные близко к остеклению, могут создавать затенения под ними, а расположенные на достаточной высоте над остеклением, мало удобны для обслуживания светильников, поэтому для обслуживания светильников используются передвижные мостики или укладываются доски на время обслуживания светильников. При обслуживании со стороны помещения стекло рассеивателя, имеющее малую массу, легко сдвигается в сторону. Кроме молочного органического стекла находят широкое применение рифленые рассеиватели.
При большой мощности ламп, размещенных в световом потолке, выделяется значительное количество тепла, для устранения которого необходимо устройство вентиляции чердака или полости, где размещены лампы.
2.1.42. Световые устройства, встроенные в стены (окна, ниши и т.п.), выполняются на тех же основаниях, которые выше рассмотрены для световых потолков.
С помощью световых окон с ЛЛ легко имитировать дневное освещение в помещениях без естественного света. Глубина световых окон обычно ограничена строительными решениями, а слепящее действие их сказывается значительно больше, чем при устройстве светового потолка той же яркости, поэтому яркость световых окон не должна превышать 250 - 500 кд/м2 и лишь в отдельных наиболее благоприятных случаях (светлый окружающий фон) - 1000 кд/м2. Наиболее благоприятное равномерное распределение яркости по светящему окну достигается при соблюдении требований п. 2.1.40. Хороший результат получается при использовании ниш отраженного света.
2.1.43. Наряду с рассеивающим органическим стеклом в световых потолках применяются экранирующие решетки, использование которых приводит к значительному снижению температуры воздуха в зоне расположения ламп. Решетки изготавливаются литьем из пластмасс или собираются из различных элементов. Для литья используется прозрачный, или замутненный полистирол, литьевое оргстекло или другие материалы. Решетку отливают в виде отдельных секций.
Экономичность осветительного устройства мало зависит от материала решетки и соотношения его коэффициентов пропускания и отражения. Значение имеет только коэффициент поглощения.
Определяющим при расчете размеров элементов решетки является заданный защитный угол. Для помещений общественных зданий защитный угол принимается равным 30° и 45°. Решетки с защитным углом 45° лучше экранируют лампы и другие монтажные элементы, поэтому имеют более декоративный вид, хотя несколько снижают КПД установки. Так как защитный угол в основном определяется отношением высоты и ширины элемента решетки, то при изменении этих элементов в равном отношении значение защитного угла остается постоянным, КПД светового потолка также не изменяется. Это позволяет выбирать размеры решеток по архитектурным и конструктивным показателям. Отметим, что мелкие ячейки создают концентрированное светораспределение, более крупные и высокие - широкое.
Основным требованием к взаимному расположению ламп и решеток, является равномерное распределение яркости по поверхности решетки, для этого необходимо, чтобы каждая планка решетки была освещена с двух сторон. При соблюдении этого требования и защитных углов решетка может иметь любой произвольный рисунок, что предоставляет широкие возможности архитекторам для создания разнообразных решеток.
2.1.44. Расчет светового потолка начинается с определения коэффициента использования светового потока источников света h, установленных над световым потолком, по формуле
где ho - коэффициент полезного действия светильников, расположенных над рассеивателем светового потолка; hТ - коэффициент использования светового потока светильников относительно отражающих поверхностей, ограничивающих пространство расположения светильников; s - отношение светопрозрачной части потолка к его общей площади, включая непрозрачные части переплетов; t - коэффициент пропускания светопрозрачного материала; hр - коэффициент использования светового потока, прошедшего через световой потолок относительно горизонтальной расчетной поверхности; hc - относительно стен.
Рис. 2.7. График зависимости коэффициента первичного использования
Для определения hр и hc пользуются графиком зависимости коэффициента первичного использования hр¢ от индекса помещения i (рис. 2.7), построенные для различных показателей т, характеризующих светораспределение элементов потолка. Кривая т = 1 предназначена для потолков из рассеивающих стекол, т = 2 - при решетках с защитным углом 30° и т = 4 - при решетках с защитным углом 45°.
Коэффициент первичного использования светового потока относительно стен hc¢ определяется по формуле:
hc¢ = 1-hр¢ (2.1.4)
Для определения значений hр и hc пользуются следующими формулами:
где hр - коэффициент первичного использования светового потока относительно расчетной поверхности; Кр.р. - коэффициент использования светового потока, падающего на расчетную поверхность, относительно расчетной поверхности; Кс.р. - коэффициент использования светового потока, падающего на стены, относительно расчетной поверхности; Кс.с. - коэффициент использования светового потока, падающего на стены относительно стен; Kp.c. - коэффициент использования светового потока, падающего на расчетную поверхность относительно стен.
Однако значения hр и hc могут быть получены и более простым путем
![]() и
и ![]() .
.
Так как коэффициенты использования потока, падающего на потолок относительно расчетной поверхности, Кп.р. или стен - Кп.с. могут рассматриваться как произведения коэффициента отражения потолка на коэффициент использования отраженного потолка в расчетной поверхности или стен (Кп.р. или Кп.с.). Оба эти метода равноценные, rп - даются только для диффузных поверхностей, при потолках из экранирующих решеток следует пользоваться формулами (2.1.5) и (2.1.6).
В формуле (2.1.3) первые четыре множителя определяются конструкцией светового потолка; hо×hТ - коэффициент использования излучателей, установленных над световым потолком, относительно потолка. Расчет этого произведения для нетиповых светильников не вызывает затруднения, а для типовых может быть определен по таблицам, на основании индекса помещения, в котором используются светильники. Если i > 5, то при светильниках прямого света произведение hо×hТ можно принимать равным КПД светильника. При высоте помещения, во много раз меньшей длины или ширины помещения, и коэффициенте отражения 0,6 и более значение hо×hТ можно считать равным 0,8. Значение коэффициента s рассчитывается по конструктивным чертежам потолка. Если между отдельными секциями со светопрозрачными элементами отсутствуют непрозрачные промежутки, то s = 0,9. Значение коэффициента t определяется свойствами светопрозрачного материала или защитным углом решетки. Его значения составят:
для молочного органического стекла - 0,63;
для экранирующей решетки с защитным углом 30° - 0,6;
то же, с защитным углом 45° - 0,45.
2.2. Административные здания
2.2.1. Для освещения помещений следует, как правило, предусматривать ЛЛ. При использовании ЛЛ следует отдавать предпочтения лампам типа ЛБ. ЛЛ другой цветности рекомендуется применять: для работ, связанных с контролем цвета, с очень высокими требованиями к цветоразличению (подбор красок для цветной печати) - лампы типов ЛХЕЦ и ЛДЦ; для сопоставления цветов с высокими требованиями к цветоразличению (картографические работы, выставочные залы, залы рассмотрения архитектурных проектов) - лампы типов ЛЕЦ, ЛДЦ и ЛХЕЦ; для общего восприятия интерьера (фойе, вестибюли) - наряду с лампами типа ЛБ также лампы типов ЛЕЦ и ЛТБЦ (лампы ЛТБЦ лучше передают цвет лица). Люминесцентные лампы мощностью 20 и 18 Вт применяются ограниченно и в основном по архитектурно-художественным соображениям (кабинеты руководителей, коридоры, холлы, вестибюли, фойе и т.п.). Наилучшие технико-экономические показатели достигаются за счет применения ЛЛ мощностью 36 Вт. В рабочих помещениях для обеспечения высоких освещенностей следует применять ЛЛ мощностью 58 и 65 Вт и 80 Вт.
2.2.2. Лампы накаливания используются в киноаппаратной, перемоточной, радиоузле, в технических помещениях без постоянного пребывания людей, в кладовых, на технических этажах и чердаках, в охлаждаемых камерах пищеблоков и т.п. Разрешается применение ЛН для обеспечения архитектурно-художественных требований в кабинетах руководителей, залах заседаний и совещаний, в фойе, выставочных залах, конференц-залах, вестибюлях. Галогенные лампы накаливания используются для освещения конференц-залов и выставочных залов.
2.2.3. Для освещения фойе, вестибюлей, конференц-залов и т.д. возможно совместное использование МГЛ и НЛВД.
2.2.4. Для освещения основных помещений могут использоваться подвесные, потолочные встраиваемые ОП с ЛЛ прямого, преимущественно прямого и рассеянного света с КСС в нижней полусфере типов Д и Г. Для рабочих помещений наиболее целесообразно применять ОП с двухлучевой КСС в поперечной плоскости (по типу полуширокой Л) с максимальным значением силы света под углами 35 - 45° и ограничением светового потока в зонах углов 0 - 30° (для снижения отраженной блескости) и 60 - 90° (для снижения прямой блескости). При выборе ОП для рабочих помещений рекомендуется использовать также ОП, часть светового потока которых направлена в верхнюю полусферу. Если позволяет высота помещения (3 м и более), целесообразно использовать подвесные ОП. При выборе потолочных ОП следует отдавать предпочтение ОП, имеющим небольшую долю светового потока в верхней полусфере (5 - 15%) со свето-рассеивающими боковинами, с выступающими из потолка рассеивателями.
2.2.5. Для освещения рабочих помещений, как правило, следует применять систему общего равномерного и локализованного освещения. Для возможности применения системы комбинированного освещения, предусмотренной нормами, в конструкторских, чертежных, проектных залах и кабинетах, читальных залах, рабочих комнатах и других помещениях следует предусмотреть сеть штепсельных розеток для осветительных приборов местного освещения.
2.2.6. Для устранения отраженной блескости, возникающей на полированной поверхности столешницы, кальке или глянцевой бумаге при конторской или чертежной работе, расположение светильников общего освещения следует выбирать в зависимости от расположения рабочих мест. Поэтому в помещениях таких зданий следует предусматривать локализованное относительно рабочих мест размещение светильников.
Светильники размещают таким образом, чтобы отраженная блескость не попадала в поле зрения работающих. Если рабочие места установлены рядами так, что линия зрения работающих направлена вдоль длинной стороны помещения, то ряды ОП с КСС типов Л, Д или Г желательно размещать вдоль линии зрения над проходами (рис. 2.8, а). Если линия зрения всех работающих направлена в одну сторону, то полного исключения прямой и отраженной блескости можно добиться, размещая ОП одностороннего светораспределения рядами, перпендикулярными линии зрения, так, чтобы световой поток падал на рабочие места из-за головы работающего (рис. 2.8, б). При отсутствии специальных ОП для этой цели можно использовать ОП прямого света с решетками с КСС типа Г, устанавливая их в наклонном положении под углами 30 - 40°. Ряд ОП над последними рабочими местами следует размещать вплотную к стене помещения. Решетка, перекрывающая выходное отверстие ОП, снизит его слепящее действие для тех, кто кратковременно изменяет направление линии зрения (например, проходит между рядами). Может быть рекомендован и другой способ размещения ОП одностороннего светораспределения - вдоль линии зрения, параллельно окнам (рис. 2.8, в). В этом случае ОП ориентируются так, чтобы их осевая сила света была направлена под углом 35 - 40° к вертикали с левой стороны от работающего.
Рис. 2.8. Взаимное расположение рабочих мест и ОП в рабочих залах:
1 - направление линии зрения работающего; 2 - преимущественное направление светового потока ОП
2.2.7. Защитой от отраженной блескости экранов мониторов является ограничение значений силы света ОП под углами, близкими к горизонтали (например, использование в качестве рассеивателя зеркалированной решетки с элементами параболического профиля).
2.2.8. При произвольном расположении рабочих мест, когда линии зрения работающих направлены в разные стороны помещения, следует применять светильники отраженного света (как исключение допускается применять световые потолки).
2.2.9. При отсутствии данных о расстановке мебели следует учитывать, что ее наиболее возможное и целесообразное размещение выполняется исходя из ориентации линии зрения вдоль стены с окнами, так чтобы естественный свет падал с левой стороны. В качестве основного способа освещения рабочих залов используется размещение ОП вдоль стен с окнами. Лучшее качество ОУ обеспечивается ОП рассеянного света типов ЛСО02, ЛСО04, ЛСО06, ЛСО05. Для освещения небольших рабочих комнат применяется также система общего равномерного освещения с направлением рядов или длинных сторон ОП вдоль линии зрения.
2.2.10. Отношения расстояния между рядами ОП к высоте их установки над освещаемой поверхностью, обеспечивающие необходимую равномерность освещения, рекомендуется принимать следующими: 0,8 - 1,2 - для ОП с экранирующими решетками; 1,2 - 1,4 - для прочих исполнений ОП. Расстояние от крайних рядов до стен не должно превышать 0,25 - 0,3 расстояния между соседними рядами.
2.2.11. Для компенсации снижения освещенности у концов рядов ОП (особенно если длина ряда более чем втрое превышает расчетную высоту) могут быть использованы следующие приемы: удвоение числа ОП на концах рядов на расстояние не менее 0,5 h установка дополнительных ОП у торцевых стен между рядами; если ОП размещены не сплошными рядами, то по мере приближения к концу ряда разрывы между ОП постепенно уменьшаются, а на концах рядов ОП устанавливаются без разрывов.
2.3. Учебные и детские дошкольные учреждения
2.3.1. Основными помещениями школ являются классные комнаты, аудитории, учебные кабинеты, лаборатории, кабинеты информатики и вычислительной техники, мастерские, кабинеты труда, актовые залы, спортивные залы, кабинеты и комнаты преподавателей. Основными помещениями дошкольных учреждений являются: раздевальные, групповые, игральные, столовые, комнаты для музыкальных и гимнастических занятий, спальные.
2.3.2. В основных помещениях зданий школ и дошкольных учреждений, как правило, следует применять систему общего освещения. Исключением является классная доска, для освещения которой следует устанавливать специальные светильники.
2.3.3. Комбинированную систему освещения следует применять в кабинетах информатики и вычислительной техники, в мастерских (например, по обработке металлов и древесины), в приемных дошкольных учреждений.
В кабинетах и комнатах преподавателей, в комнатах кружков, читальных залах для МО следует предусматривать штепсельные розетки.
2.3.4. Общее локализованное освещение допускается применять в помещениях, где рабочие места расположены группами (например, различного рода мастерские, кабинеты домоводства, зоны психологической разгрузки учащихся).
2.3.5. Для общего и общего локализованного освещения следует использовать, как правило, энергоэкономичные люминесцентные лампы мощностью 18, 36 и 58 Вт, компактные люминесцентные лампы мощностью 18, 24 и 36 Вт:
- в помещениях, где производится сопоставление цветов с высокими требованиями к цветоразличению (кабинеты рисования, обслуживающих видов труда, лаборатории химии ) - типов ЛЕЦ, ЛХЕ, ЛБЦТ;
- в помещениях, где производится различение цветных объектов при невысоких требованиях к цветоразличению (кабинеты кружков, игральные, обеденные залы, крытые бассейны, спортзалы) - типов ЛБ, ЛБЦТ, КЛЛ, ЛХБ;
- в помещениях, где требования к цветоразличению отсутствуют (классные комнаты, аудитории, учебные кабинеты, библиотеки, раздевальные, групповые) - типов ЛБ, ЛХБ, КЛЛ;
- (актовые залы, вестибюли, рекреации) - типов КЛТБЦ, ЛТБЦ, ЛЕЦ.
2.3.6. Лампы накаливания следует применять для освещения вспомогательных помещений - насосных, тепловых пунктов, бойлерных, электрощитовых, технических подполий. Допускается использование ламп накаливания, в том числе галогенных и зеркальных для освещения актовых залов и эстрад в соответствии с архитектурным решением интерьера.
2.3.7. Для общего освещения учебных помещений школ следует применять светильники преимущественно прямого и рассеянного света. Светильники рекомендуется размещать рядами, параллельно длинной стороне помещения с окнами с раздельным включением и отключением рядов. Ряды должны быть по возможности непрерывными или с разрывами, не превышающими 0,5 расчетной высоты.
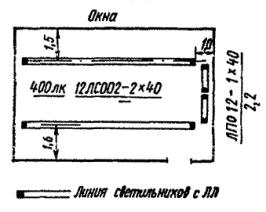
Рис. 2.9. Схема размещения светильников в классе
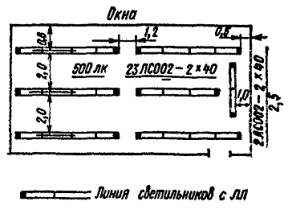
Рис. 2.10. Схема размещения светильников в кабинете черчения и рисования
2.3.8. Для освещения классной доски рекомендуется применение светильников с несимметричным светораспределением, например ЛПО 12 1´40, размещенными параллельно плоскости доски либо непосредственно над доской, либо установленными на потолке. Допускается освещение классной доски светильниками прямого света, установленными наклонно.
2.3.9. Для общего освещения кабинетов информатики и вычислительной техники следует применять светильники с защитными углами 35 - 45°, размещенными по потолку рядами, параллельно светопроемам. Рабочие места с дисплеями должны располагаться между рядами светильников таким образом, чтобы линия зрения пользователей была параллельна световым линиям. Яркость светильников в пределах защитного угла, попадающих в поле зрения пользователей или отражающихся в экране монитора не должна превышать 200 кд/м2. Максимальная яркость поверхностей в помещении не должна превышать 400 кд/м2. При устройстве комбинированного освещения светильник местного освещения должен использоваться исключительно для освещения горизонтальной поверхности стола. Защитный угол светильника местного освещения должен быть не менее 40°.
2.3.10. Для освещения кабинетов технического черчения и рисования следует применять светильники преимущественно прямого и рассеянного света с КПД не менее 55%.
2.3.11. Освещение актовых залов, как правило, следует выполнять рядами светильников с люминесцентными лампами. Для обеспечения благоприятных условий тенеобразования на объемных предметах и лицах людей в интерьере отношение Егор./Ецил. должно быть в пределах 1,6 - 3.
2.3.12. Освещение эстрад или сцен следует, как правило, выполнять светильниками акцентирующего освещения с галогенными или зеркальными лампами накаливания, устанавливаемыми на потолке или на боковых стенах. Источники света в светильниках должны быть скрыты от глаз зрителей.
2.3.13. В читальных залах библиотек следует применять систему общего освещения рядами светильников с люминесцентными лампами. Для подключения переносной аппаратуры (диапроекторов) необходимо предусматривать розетки. Освещение книгохранилищ следует выполнять светильниками, устанавливаемыми по оси каждого прохода между стеллажами, светильники не должны мешать доступу к книжным полкам. Исполнение светильников должно выбираться в соответствии с требованиями, установленными в пожароопасных зонах класса II-IIa (см. п. 2.1.16 настоящего пособия).
2.3.14. Для освещения крытых бассейнов следует использовать брызгозащищенные светильники с диффузными рассеивателями прямого или преимущественно прямого света, установленными на потолке или стенах над боковыми проходами. Места расположения светильников должны находиться в зоне, доступной для обслуживания.
2.3.15. Освещение спортивных залов следует выполнять светильниками с люминесцентными лампами, установленными на потолке вдоль боковых стен или наклонно по боковым стенам. Предпочтительны осветительные установки отраженного света. Для защиты от удара мячом светильники следует закрывать металлическими решетками.
2.3.16. Для освещения помещений дошкольных учреждений следует, как правило, использовать светильники рассеянного света, допустимы светильники преимущественно прямого света. Следует отдавать предпочтение равномерной кривой силы света (типа М), допустимы полуширокая (типа Л ) и косинусная (типа Д) кривые сил света.
Как пример, на рис. 2.11 даны размещение ОП и схема групповой сети освещения в ячейке детского сада-яслей, состоящей из раздевальной, групповой и спальни.
Рис. 2.11. Условная схема размещения светильников в ячейки детского сада-яслей
2.3.17. Значения коэффициентов отражения парт, потолка, стен и пола должны быть не менее 0,4; 0,7; 0,5; 0,3.
2.3.18. Классная доска, деки парт и игровые столы для дошкольников не должны быть темными. Соотношения яркостей между отдельными поверхностями, находящимися в поле зрения учащихся, не должны превышать следующих соотношений: между книгой, тетрадью и декой парты 3:1, между тетрадью, книгой и дальним фоном (стеной, полом) - 10:1, между светильником и его фоном - 20:1.
2.3.19. Для обеспечения комфортных условий в помещении из поля зрения учащихся следует исключать зеркально отражающие поверхности.
2.3.20. Для создания комфортной световой среды стены и потолки помещений дошкольных учреждений рекомендуется окрашивать матовыми красками светлых тонов с коэффициентами отражения : потолки - 70%, стены - 50 - 60%.
2.3.21. Для соблюдения нормируемых СНиПом значений коэффициентов пульсации и снижения уровня шумов в учебных помещениях (классах, кабинетах, лабораториях) и помещениях дошкольных учреждений (групповые, игральные, комнаты для музыкальных занятий), как правило, следует применять светильники с электронными пускорегулирующими аппаратами. Допускается использование многоламповых светильников с электромагнитными пускорегулирующими аппаратами, состоящими из равного числа опережающих и отстающих ветвей и равного числа ламп.
2.3.22. Эвакуационное освещение в учебных зданиях следует устраивать по основным проходам, в рекреациях, на лестничных клетках, в мастерских, гардеробных, актовых залах, обеденных и спортивных залах, плавательных бассейнах, вестибюлях. В классах, кабинетах эвакуационное освещение не требуется. В зданиях дошкольных учреждений эвакуационное освещение следует устраивать в групповых, игральных-столовых, приемных, раздевальных, коридорах, на лестничных клетках, в кухнях и стирально-разборочных независимо от числа детей. Эвакуационное освещение должно обеспечивать освещенность на полу основных проходов и на ступеньках лестниц не менее 0,5 лк, на поверхности воды ванн бассейнов для плавания не менее 5лк.
2.3.23. Для дежурного освещения и освещения для уборки коридоров, залов, вестибюлей и других подобных помещений следует выделять часть светильников рабочего освещения, присоединяемых к отдельной групповой линии. В актовых и обеденных залах и других помещениях, где могут одновременно пребывать более 100 человек, должны устанавливаться световые указатели «Выход», подключаемые к отдельной линии аварийно-эвакуационного освещения или имеющие аккумуляторную батарею.
2.3.24. Для дежурного (ночного) освещения спальных помещений, помещений для заболевших детей и в палатах изоляторов детских садов-яслей и школ-интернатов следует применять специальные светильники со стеклом синего цвета и экранирующей решеткой, присоединенные к сети аварийного освещения. При установке этих светильников (вблизи от выходов) на высоте, доступной для детей, должно применяться напряжение не более 42 В.
2.3.25. Для обслуживания светильников в актовых и спортивных залах, высота которых превышает 5 м, следует предусматривать в проектах передвижные телескопические вышки и выделять помещения для их хранения.
2.3.26. Контроль освещенности в учебных помещениях следует проводить один раз в год. Регламентные работы (чистка и ремонт светильников, замена источников света) рекомендуется проводить один раз в два года. В учебных помещениях с высотой потолка не более 4 м источники света заменяются по мере выхода их из строя.
2.4. Лечебно-профилактические учреждения
2.4.1. Освещение лечебно-профилактических учреждений следует проектировать с учетом требований МГСН 4.12-97 по проектированию лечебно-профилактических учреждений.
2.4.2. Световая среда лечебных учреждений помимо обеспечения условий работы медицинского персонала должна удовлетворять требованиям психофизиологического климата, способствующего выздоровлению больных. Одним из этих требований является обеспечение комфортности освещения палат: пятна повышенной яркости (источники света и блеские части светильников) не должны попадать в поле зрения больных, находящихся в горизонтальном положении. Это обеспечивается использованием схемы распределения света светильниками, показанной на рис. 2.12 а) и б).
Рис. 2.12. Схема распределения света в палате лечебного учреждения
а) - потолочным и местным светильниками; б) - комбинированными прикроватными светильниками
Выполнение схем а) и б) осуществляется применением системы комбинированного освещения, практически рекомендуемой для всех помещений палат, за исключением послеоперационных, детских и психиатрических отделений. Световой поток направляется на потолок и вниз в центр комнаты, а зона изголовий кровати остается затененной. Дополнительно над кроватями на стенах устанавливаются светильники с отражателями (рис. 2.13). Каждый светильник состоит из двух отражателей, свет от одного из которых направляется на потолок для общего отраженного освещения, а другого используется для МО изголовий. Удобны светильники, прикрепляемые непосредственно к кровати. Такие, светильники могут быть использованы и как переносные при осмотре больных. Светильники, изображенные на рис. 2.13 обеспечивают больным возможность читать в лежачем положении.
2.4.3. Для обеспечения нормированной освещенности в помещениях больничного комплекса применяется система общего освещения, при которой светильники общего освещения могут размещаться на потолке и на стенах равномерно или локализованно. Система общего освещения с равномерным расположением светильников применяется в кабинетах врачей, процедурных, регистратуре и др. Система общего локализованного освещения используется в помещениях, где требуется повышенная освещенность отдельных участков.
Светильники МО предназначаются только для освещения рабочих мест и могут быть стационарными и переносными. Стационарные светильники устанавливаются в процедурных, смотровых, операционных, кабинетах физиотерапии и т.п.
Настенные светильники монтируют на высоте 1,7 м от пола. В кабинетах врачей предусматриваются розетки для включения светильников МО, устанавливаемых на высоте 0,9 м от пола.
2.4.4. Специальные требования предъявляются к освещению операционных в целях создания высокой освещенности и одновременно исключения теней от рук и головы хирурга и не допущения теплового нагрева оперируемого и головы хирурга.
Рис. 2.13. Схема светильников для больничных палат
Рис. 2.14. Светильник типа «Свет 15»
Для освещения операционных широкое распространение получили светильники типа «Свет-15» (рис. 2.14), в которых каждый источник света перекрыт теплопоглощающим фильтром. Такие светильники обеспечивают на операционном поле освещенность 10000 - 50000 лк. Освещенность может регулироваться изменением расстояния от светильника до оперируемого больного. Высокая освещенность обеспечивает возможность получить качественные изображения на телеэкране. При применении бестеневых светильников типов СРСА-6, СМ-36 и СМТ-34 пульт управления устанавливается в аппаратной.
Кроме специального освещения стола операционная должна иметь общее освещение. Оно может создаваться потолочными светильниками с ЛЛ брызгозащищенного исполнения со сплошным закрытым рассеивателем из опалового молочного или матового стекла (типа ЛПО25). Кроме общего освещения для подключения специальных передвижных осветительных приборов предусматривается установка двухполюсной розетки на высоте 1,6 м.
Для продолжения операции при аварийном отключении рабочего освещения следует предусматривать аварийное освещение включением части ламп светильника «Свет-15» в сеть аварийного освещения. Питание аварийного освещения осуществляется от независимого источника энергии, обычно от аккумуляторных батарей, на которые автоматически переключается сеть аварийного освещения при аварии с основным источником электроснабжения.
2.4.5. Кроме операционной аварийное освещение следует предусматривать в реанимационных, родовых, перевязочных, манипуляционных, процедурных приемных отделениях, лабораториях для срочных анализов и на постах дежурных медицинских сестер, пунктах неотложной помощи, в тепловых пунктах, насосных, электрощитовых. Аварийное освещение осуществляется стационарными светильниками с ЛН или ЛЛ. Для ночного дежурного освещения палат, кроме палат психиатрических и детских отделений, следует предусматривать светильники (например, типа ДС-19), расположенные в специальных нишах на высоте 0,3 м от пола. В детских, послеоперационных, реанимационных, интенсивной терапии и психиатрических палатах предусматривается только общее освещение потолочными ОП со сплошными рассеивателями.
2.4.6. Общее освещение помещений, как правило, следует выполнять ЛЛ. Осветительные приборы с ЛЛ должны быть укомплектованы ПРА с особо низким уровнем шума.
2.4.7. Для освещения помещений, предназначенных для осмотра больных (инфекционных, дерматологических, дерматовенерологических, операционных, хирургических, терапевтических, педиатрических и т.д.) следует использовать ЛЛ типов ЛЕ и ЛХЕ.
2.4.8. Для освещения помещений, предназначенных для приготовления пищи, административных, коридоров, вестибюлей и других помещений следует применять ЛЛ типа ЛБ.
2.4.9. В кабинетах хирургов, травматологов, педиатров, дерматовенерологов, инфекционистов, аллергологов, стоматологов, врачей-лаборантов рекомендуется применять потолочные полностью закрытые (например, ЛПО02, НПО 18) светильники. В кабинетах врачей специалистов функциональной диагностики рекомендуются светильники преимущественно с ЛН, например, НПО18. Для местного освещения используются настольные или настенные светильники.
Освещение помещений, предназначенных для осмотра больных, административных помещений, коридоров, вестибюлей, лестничных клеток и т.п. обеспечивается потолочными или встраиваемыми светильниками с ЛЛ, монтируемыми отдельно или полосами. Для выполнения гигиенических и светотехнических требований светильники должны быть перекрыты сплошными рассеивателями во избежание запыления и для обеспечения стерильных условий (например, типов ЛПО31, ЛПО02, ЛПО01 и др.).
2.4.10. Общее освещение рентгенодиагностического кабинета, кабинетов рентгенобронхоскопии, лапароскопии, ангиографии выполняется светильниками с ЛН (например НПО18), кроме того кабинеты оборудуются настенными светильниками (НБО06). Кабинеты рентгенодиагностического отделения оборудуются световой сигнализацией.
Все кабинеты оборудуются розетками для подключения настольных ОП. Общее освещение кабинетов рентгенодиагностики, рентгенобронхоскопии, лапароскопии выполняется закрытыми ОП только с ЛН. В офтальмологических кабинетах выполняется два вида освещения - общее и специальное.
Рентгенодиагностические кабинеты снабжаются кроме общего адаптационным и местным освещением. Адаптационное освещение выполняется установкой в центре кабинета ОП с ЛН мощностью 60 Вт, управляемого врачом. Входы в кабинеты снабжаются световыми указателями с надписью «Не входить», устанавливаемыми над входными дверями и управляемыми врачом.
2.4.11. Для обеззараживания воздуха в операционных, перевязочных, инфекционных отделениях больниц, в приемных родильных домов следует устанавливать бактерицидные облучатели (например, типа ОБП-300).
2.4.12. Эвакуационное освещение необходимо в коридорах, вестибюлях, на лестничных клетках.
2.4.13. Световые указатели с надписью «Выход» следует устанавливать у входов на лестничные клетки и у выходов с первого этажа и из подвалов. Световые указатели направления выходов следует предусматривать в коридорах.
2.5. Предприятия торговли
2.5.1. Основными помещениями предприятий торговли являются торговые залы, залы демонстрации новых товаров и фасонов одежды, примерочные кабины, помещения отделов заказов, бюро обслуживания, помещения для подготовки товаров к продаже, главные кассы, мастерские подгонки готового платья, рекламно-декорационные и ремонта оборудования и инвентаря.
2.5.2. Для общего и общего локализованного освещения помещений предприятий торговли, а также для подсветки товаров следует использовать, как правило, люминесцентные лампы, возможно применять ДРИ и ДРИ совместно с ДНаТ. В ряде случаев, когда целесообразны лампы накаливания следует применять зеркальные или галогенные лампы накаливания. Рекомендации по выбору типа люминесцентных ламп в зависимости от вида товара приведены в табл. 2.5.1, для подсветки внутренних витрин - в табл. 2.5.2.
Таблица 2.5.1
|
Тип люминесцентных ламп |
|
|
Магазины: |
|
|
тканей, готового платья, парфюмерии, галантереи, игрушек, цветов |
ЛДЦ, ЛХЕ, ЛДЦУФ |
|
обуви, спортивных товаров, ювелирные |
ЛБ, ЛБЦТ, КЛЛ, ЛЕЦ |
|
головных уборов, книжные и канцтоваров |
ЛБ |
|
примерочные кабины, бракеражные столы |
ЛДЦ, ЛХЕ, ЛДЦУФ |
|
Торговые залы магазинов: |
|
|
мебельных |
ЛБЦТ, ЛЕЦ, ЛДЦ |
|
посудо-хозяйственных, электротоваров |
ЛБ |
|
меховых изделий |
ЛЕЦ, ЛДЦ, ЛБ, ЛБЦТ |
|
Торговые залы магазинов: |
|
|
универсальные, «мясо», «птица», «гастрономия», «молоко», «овощи» |
ЛЕЦ |
|
«рыба» |
ЛДЦ |
|
«бакалея», «хлеб», «кондитерские изделия», «вино» |
ЛБ |
Таблица 2.5.2
|
Тип люминесцентных ламп |
|
|
Ткани, верхняя одежда, парфюмерия, игрушки, книги, спорттовары, обувь, головные уборы, меха |
ЛБЦТ, ЛХЕ, ЛДЦ, ЛЕЦ |
|
Электротовары, посудохозяйственные и канцелярские товары |
ЛБ |
|
Мясные, молочные, гастрономические, овощные продукты, кондитерские изделия |
ЛЕЦ |
|
Рыбные продукты |
ЛДЦ |
|
Бакалея, хлеб |
ЛБ |
2.5.3. Для общего освещения торговых залов следует применять потолочные, подвесные, настенные и встраиваемые в потолок светильники с люминесцентными лампами, в том числе компактными, освещающими стены помещений. Возможно использование световодов и световых потолков с МГЛ. В ряде случаев целесообразно применять светильники с галогенными лампами накаливания и отдельно галогенные лампы накаливания с отражателями мощностью 50 - 100 Вт на 12 В, установленные на шинопроводе.
Допускается использование нестандартных, разработанных по эскизам архитекторов светильников.
2.5.4. Освещение вертикальных поверхностей торговых стендов и витрин следует выполнять светильниками с зеркальными отражателями или зеркальными лампами с концентрированным и глубоким симметричным светораспределением.
2.5.5. При устройстве комбинированного освещения светильники местного освещения, как правило, следует встраивать в торговое оборудование или пристраивать к нему, при этом конструкция торгового оборудования должна экранировать источник света от покупателей.
2.5.6. В качестве информационных указателей, табло в крупных магазинах возможно использование одноламповых или двухламповых светильников с люминесцентными лампами, имеющих молочные рассеиватели.
2.5.7. Для освещения ювелирных магазинов, как правило, используется система комбинированного освещения, при местной подсветке светильниками акцентирующего освещения с лампами накаливания или галогенными лампами, экранированными от покупателей.
2.5.8. Освещение примерочных кабин следует выполнять светильниками, установленными выше зеркала, чтобы свет падал на грудь человека под углом 30 - 45° к вертикали.
2.5.9. При освещении помоста залов для демонстрации моды рекомендуется использовать светильники прямого света, обеспечивающие необходимое тенеобразование верхним и верхнебоковым светом.
2.5.10. Освещение кассовых кабин при недостаточности общего освещения следует выполнять подвесным светильником, либо пристраиваемым к оборудованию светильником, установленным слева над кассовым аппаратом.
2.5.11. Освещение в наружных, витринах предприятий торговли, как правило, следует выполнять осветительными устройствами и светильниками преимущественно прямого светораспределения, размещенными в верхней зоне витрин. Местное освещение товаров следует осуществлять светильниками концентрированного или глубокого светораспределения, установленными на полу или на потолке витрины у наружного остекления, либо на импостах витрины.
2.5.12. При местном освещении особо ценных товаров (ювелирные изделия), расположенных в витрине, следует использовать систему волоконных световодов.
2.5.13. При небольшой высоте помещений киосков и палаток, освещение в них следует выполнять потолочными светильниками с непрозрачными боковинами и светорассеивающей экранирующей решеткой. Светильники размещаются над прилавками и товарной продукцией. Светильники должны соответствовать требованиям норм пожарной безопасности.
2.5.14. Во всех магазинах предусматривается рабочее освещение. В магазинах с торговыми залами общей площадью 90 м2 и более, в торговых залах и по путям выхода из них оборудуется эвакуационное освещение. Во всех торговых залах самообслуживания также устраивается аварийное освещение. Аварийное освещение предусматривается в крупных магазинах в помещениях главной кассы, АТС, радиоузле, здравпункте, детской комнате и дебаркадере.
2.5.15. В складских и административных помещениях магазинов, а также в отдельных складских зданиях в случае пребывания в них одновременно более 50 человек, а также в местах, опасных для прохода людей, следует предусмотреть эвакуационное освещение.
2.5.16. В торговых залах, расположенных на первых этажах магазинов, и по путям эвакуации из них следует предусматривать ночное охранное освещение. В крупных торговых предприятиях целесообразна сеть ночного освещения, контролируемого из помещений охраны специальным подразделением милиции.
2.5.17. Выходы из магазинов с торговыми залами общей площадью 180 м2 и более, а при самообслуживании - с торговыми залами 110 м2 и более должны быть отмечены световыми указателями с надписью «Выход».
2.5.18. Управление рабочим освещением в торговых залах площадью от 300 м2 и более должно быть централизованным дистанционным.
2.5.19. Управление освещением световых указателей, входов в здание, номерных знаков должно быть автоматическим или дистанционным.
2.5.20. Для обслуживания светильников в актовых и спортивных залах, высота которых превышает 5 м, следует предусматривать в проектах передвижные телескопические вышки и выделять помещения для их хранения.
2.6. Предприятия общественного питания
2.6.1. Для общего, общего локализованного и комбинированного освещения помещений для посетителей следует использовать, как правило, энергоэкономичные люминесцентные лампы; в том числе компактные типов ЛБ, ЛБЦТ, КЛЛ, ЛЕЦ. Допускается использование ламп накаливания, в том числе галогенных и зеркальных для освещения ресторанов, кафе, баров. Возможны комбинации люминесцентных ламп и ламп накаливания.
2.6.2. Локализованное освещение над баром или буфетной стойкой следует выполнять потолочными, встраиваемыми или подвесными светильниками. В отдельных зонах залов ресторанов возможно применение подвесных и встраиваемых светильников, устанавливаемых над столами, а также светильников местного освещения, устанавливаемых на столах, напольных и настенных светильников.
2.6.3. В ресторанах, барах и кафе, где предусмотрены выступления ансамблей и танцевальные площадки, следует осуществлять постановочное освещение согласно ВСН 59-88.
2.6.4. В производственных помещениях следует применять светильники с люминесцентными лампами, как правило, типа ЛБ. Размещение светильников должно быть увязано с размещением воздуховодов вентиляции. В горячих цехах не следует размещать светильники непосредственно над тепловым оборудованием (плиты, котлы и т.д.). Исполнение светильников должно выбираться в соответствии с требованиями к условиям среды, установленными в п. 2.1.16 настоящего пособия.
2.6.5. Светильники с люминесцентными лампами, устанавливаемые над рабочими местами в помещениях для приготовления и раздачи пищи (столы, плиты и т.п.) должны иметь снизу защитное стекло, решетку или специальные патроны, конструкция которых исключает возможность выпадения ламп.
2.6.6. В складских помещениях (кладовых), где находятся продукты в сгораемой упаковке, следует, применять светильники с лампами накаливания, имеющими замкнутый рассеиватель из силикатного стекла. Запрещается применение светильников с отражателями и рассеивателями из горючих материалов.
2.6.7. При проектировании освещения административных и бытовых помещений следует руководствоваться рекомендациями, изложенными в разделах «Административные здания» и «Предприятия бытового обслуживания» данного пособия.
2.6.8. В помещениях предприятий общественного питания следует предусматривать эвакуационное освещение:
- в проходных помещениях и на лестницах, служащих для эвакуации людей из предприятий, где работает или находится одновременно более 50 человека;
- в обеденных залах, в которых одновременно могут быть более 100 человек;
- в производственных помещениях (горячие и холодные цеха и т.п.).
2.6.9. Необходимо предусмотреть устройство аварийного освещения в электрощитовых, диспетчерских, насосных с постоянным дежурным персоналом, главных кассах, дебаркадерах крупных предприятий.
2.6.10. Выходы из обеденных залов, вестибюлей и других, помещений, рассчитанных на одновременное пребывание более 100 человек, а также выходы из коридоров, к которым примыкают помещения, где могут одновременно находиться более 50 человек, должны иметь световые указатели с надписью «Выход», подключаемые к отдельной линии аварийно-эвакуационного освещения или имеющие аккумуляторную батарею.
2.6.11. Для энергоэкономичных и безопасных осветительных установок целесообразно предусматривать управление освещением в соответствии с таблицей 2.5.3.
Таблица 2.5.3
|
Способ управления общим освещением |
Дополнительные требования |
|
|
1 |
2 |
3 |
|
Вестибюль, лестничная клетка |
В крупных предприятиях - централизованное с центрального диспетчерского пульта, в остальных централизованное из зоны с постоянным обслуживанием |
- |
|
Залы ресторана, кафе, бара* |
Централизованное с пульта управления |
- |
|
То же, а также залы столовой, закусочной и т.п.* |
При отсутствии пульта - централизованное из зоны с постоянным обслуживанием |
При нерегулируемом освещении предусматривать 2-3 ступени включения. |
|
Производственное, административно-бытовое |
Местное |
Не допускается установка выключателей внутри помещений горячих цехов, кладовых, душевых, преддушевых, туалетов |
|
Склад и кладовая |
Местное для каждого помещения, но с централизованным отключением по окончании работы |
Выключатели местного управления освещением должны быть расположены вне помещения на несгораемых конструкциях и заключены в коробки (шкафы) или ниши с приспособлением для опломбирования |
* Аппараты управления освещением должны быть недоступны для посетителей
2.7. Предприятия бытового обслуживания
2.7.1. В помещениях для посетителей, в производственных помещениях для изготовления и ремонта одежды, меховых и трикотажных изделий, головных уборов, в производственных помещениях химической чистки, в парикмахерских залах следует применять ЛЛ типов ЛДЦ и ЛХБ. В моечных, душевых, парильных в банях следует применять ЛН. Для остальных помещений рекомендуется использовать ЛЛ типа ЛБ.
2.7.2. Светильники в мокрых и влажных помещениях должны быть герметичными и брызгозащищенными (см. п. 2.1.16).
2.7.3. Над гладильными установками и рабочими столами для сортировки и раскладки грязного и чистого белья следует предусматривать локализованное размещение светильников на высоте 2 - 2,5 м от рабочих поверхностей. Локализованное размещение светильников следует предусматривать также в пошивочных и ремонтных мастерских.
2.7.4. В помещениях граверных работ, ремонта часов, телевизоров, радиоаппаратуры, обуви, металлоизделии, в химчистке на столе приемщицы и др. следует применять систему комбинированного освещения.
2.7.5. В производственных цехах прачечных, в вестибюлях, коридорах, ожидальных, раздевальных, мыльных, душевых, парильных, помещениях бассейнов и на лестничных клетках необходимо предусматривать эвакуационное освещение.
2.7.6. Для охранного освещения следует использовать светильники эвакуационного освещения.
2.8. Гостиницы
2.8.1. При проектировании ОУ гостиниц необходимо участие архитектора и светотехника в выборе ОП.
2.8.2. Освещение основных помещений гостиниц следует, как правило, выполнять ЛЛ. При специальном архитектурном решении помещения допускается применение ЛН.
2.8.3. В жилых помещениях освещение должно проектироваться с соблюдением принципа зональности. Для освещения каждой из зон (работы, отдыха, сна) должны предусматриваться различные, обычно переносные ОП, совместное действие которых должно обеспечивать нормируемую среднюю освещенность.
В качестве ОП общего освещения могут использоваться подвесные, потолочные или настенные ОП: Наиболее традиционным решением является размещение в центре комнаты подвесного одно- или многолампового ОП желательно рассеянного или преимущественно отраженного света. Менее желательны, хотя и возможны, ОП преимущественно прямого (из-за небольшой доли светового потока в верхнюю полусферу) и отраженного (из-за невысокой экономичности) света, а также потолочные ОП (из-за небольшой доли светового потока на потолок). Значительно реже используются настенные ОП на одну-две ЛН, размещаемые на длинной стене гостиной. Для большей равномерности освещения целесообразно установка двух настенных ОП.
Недопустима установка в жилых комнатах осветительных приборов, предназначенных для освещения административных помещений общественных зданий. Такое решение лишит номер уюта, придаст помещению официальный канцелярский вид. Более уместным является установка местных осветительных приборов с компактными или фигурными ЛЛ типа ЛТБЦ.
2.8.4. В номерах гостиниц следует предусматривать дополнительное местное освещение (бра, настольная лампа, торшер и т.д.). Использование для общего освещения номеров гостиниц и других помещений напольных светильников (торшеров) допускается как исключение.
2.8.5. В ванной комнате рекомендуется устанавливать светильники-плафоны с ЛН или ЛЛ типа ЛТБЦ над зеркалом, в уборной с ЛН над дверью. У умывальников должны устанавливаться штепсельные розетки для электробритв.
2.8.6. Для освещения коридоров могут быть использованы системы общего (как равномерного, так и локализованного) или комбинированного освещения. Размещение ОП с ЛЛ длинной стороной вдоль коридора является предпочтительным, поскольку при этом увеличивается доля светового потока, первоначально падающего на стену.
Локализованное общее освещение может выполняться неравномерной установкой потолочных ОП с учетом расположения дверей, например, при размещении номеров с одной стороны коридора - смещением потолочных ОП с осевой линии к стене с дверями, а при размещении дверей с обеих сторон коридора - «шахматной» установкой ОП. Локализованное освещение коридоров может выполняться ОП, встраиваемыми в дверную коробку каждого номера, что значительно увеличивает вертикальную освещенность полотна двери и при соответствующей мощности ОП, например, 2´18 Вт при двустороннем расположении номеров вполне достаточно для создания нормируемой освещенности на полу коридора.
2.8.7. В ванных комнатах и уборных светильники должны иметь корпус из изолирующих влагостойких материалов.
2.8.8. В холле должны предусматриваться штепсельные розетки для включения напольного или настольного ОП, телевизора.
2.8.9. Аварийное освещение утраивается в вестибюлях и гардеробах, эвакуационным освещением оборудуются коридоры и лестницы, служащие для эвакуации более 50 человек. Световые указатели «Выход» устанавливаются над дверями, ведущими на лестницы, в вестибюль и на улицу. В коридорах длиной более 25 м световыми указателями отмечаются направления к выходу. Кроме указанных помещений устройствами эвакуационного освещения оборудуются и другие помещения, расположенные в гостинице (см. п. 2.1.5 - 2.1.7).
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. СНиП 23-05-95. Естественное и искусственное освещение. - М.: ГП ЦПП, 1995.
2. МГСН 2.06-99. Естественное, искусственное и совмещенное освещение. -М.:ГУП «НИАЦ», 1999.
3. МГСН 2.01-99. Энергосбережение в зданиях. Нормативы по теплозащите и тепловодоэлектроснабжению. - М.:ГУП «НИАЦ », 1999.
4. МГСН 4.12-97. Лечебно-профилактические учреждения. М.:-ГУП «НИАЦ », 1998.
5. ГОСТ 24940-96. Здания и сооружения. Методы измерения освещенности.
6. ГОСТ 17677-82. Светильники. Общие технические условия.
7. ГОСТ 8607-82. Светильники для освещения жилых и общественных зданий. Общие технические условия.
8. ГОСТ 14254-80. Оболочки. Системы защиты.
9. ВСН 59-88. Электрооборудование жилых и общественных зданий. Нормы проектирования. - М: Стройиздат, 1990.
10. Пособие по расчету и проектированию естественного, искусственного и совмещенного освещения. - М.: Стройиздат, 1985.
11. Кнорринг Г.М., Фадин И.М., Сидоров В.Н. Справочная книга для проектирования электрического освещения. - С-Пб.: Энергоатомиздат, 1992.
12. Справочная книга по светотехнике. Под ред. Ю.Б. Айзенберга - 2-е изд., - М.: Энергоиздат, 1995.
13. Герсонская В.И. Таблицы удельной мощности для светильников прямого света с типовыми кривыми силы света. - Светотехника, 1986. № 8.
14. Шмаров И.А. Применение свойств сферической симметрии светового поля в светотехнических расчетах. - Вестник отделения строительных наук РААСН. Выпуск 2, 1999.
15. Правила устройства электроустановок. Раздел VI. Электрическое освещение.
ИСПОЛЬЗУЕМЫЕ АББРЕВИАТУРЫ
ЛЛ - люминисцентные лампы
МГЛ - металлогенные лампы
НЛВД - натриевые лампы высокого давления
ОЛ - осветительные приборы
КСС - кривая силы света
ПРА - пускорегулирующая аппаратура
ЛН - лампы накаливания
ОУ - осветительная установка
МО - местное освещение