РАГС - РОССИЙСКИЙ АРХИВ ГОСУДАРСТВЕННЫХ СТАНДАРТОВ, а также строительных норм и правил (СНиП)
и образцов юридических документов
Произвольная ссылка:
ГОСТ 8.381-80 Государственная система обеспечения единства измерений. Эталоны. Способы выражения погрешностей.

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ
ЕДИНСТВА ИЗМЕРЕНИЙ
ЭТАЛОНЫ
СПОСОБЫ ВЫРАЖЕНИЯ ПОГРЕШНОСТЕЙ
ГОСТ 8.381-80
(СТ СЭВ 403-76)
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
Москва
РАЗРАБОТАН Государственным комитетом СССР по стандартам
ИСПОЛНИТЕЛИ
М. Н. Селиванов, канд. техн. наук; Б. Ф. Лосев, канд. техн. наук
ВНЕСЕН Государственным комитетом СССР по стандартам
Член Госстандарта Л. К. Исаев
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 13 мая 1980 г. № 2087
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
|
ЭТАЛОНЫ Государственная система обеспечения
единства State system
for ensuring
the uniformity of measurements. |
ГОСТ (СТ СЭВ 403-76) |
Постановлением Государственного комитета СССР по стандартам от 13 мая 1980 г. № 2087 срок введения установлен
с 01.01 1981 г.
Настоящий стандарт распространяется на эталоны СЭВ, государственные первичные (специальные) и вторичные эталоны и устанавливает способы выражения их погрешностей в нормативно-технической документации в области метрологии.
Стандарт соответствует СТ СЭВ 403-76 в части установления общих положений, способов выражения погрешностей эталонов и обозначений (см. справочное приложение 5).
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Погрешность эталонов СЭВ и государственных первичных (специальных) эталонов (далее - первичных эталонов) характеризуется:
неисключенной систематической погрешностью;
случайной погрешностью;
нестабильностью.
Допускается указывать случайную погрешность воспроизведения единицы с учетом передачи ее размера или последнюю указывать отдельно.
1.2. Оценку неисключенной систематической погрешности первичного эталона находят на основании экспериментальных данных исследований эталона, анализа погрешностей метода воспроизведения единицы и погрешностей от действия влияющих величин, а также на основании международных сличений эталона с эталонами других стран и с эталоном СЭВ, если он имеется.
1.3. Оценку случайной погрешности первичного эталона находят на основании экспериментальных данных, полученных при исследовании эталона, и на основе анализа влияющих величин.
1.4. Оценку нестабильности первичного эталона, вызываемую влиянием старения его отдельных элементов и другими причинами, находят на основании исследований эталона во времени, а также по данным периодических международных сличений.
1.5. В оценку погрешности передачи размера единицы должны входить как неисключенные систематические, так и случайные погрешности метода и средств передачи.
1.6. Оценки погрешности вторичных эталонов должны характеризовать отклонения размеров хранимых ими единиц от размера единицы, воспроизводимой при помощи первичного эталона.
Для вторичного эталона указывают суммарную погрешность, включающую случайные погрешности сличаемых эталонов и погрешность передачи размера единицы от первичного (или более точного вторичного) эталона, а также нестабильность вторичного эталона.
Допускается суммарную погрешность вторичного эталона определять с учетом его неисключенной систематической погрешности.
Допускается указывать отдельно неисключенную систематическую погрешность вторичного эталона, а также его нестабильность.
По требованию заказчика могут быть указаны отдельно и другие составляющие погрешности вторичного эталона.
1.7. Нестабильность вторичного эталона должна определяться на основании сличений с первичным эталоном в начале и конце периода, для которого она определяется.
1.8. Оценку погрешности эталонов следует указывать либо в абсолютной форме в единицах измеряемой величины, либо в относительной форме.
Примечание. Если зависимость погрешности от значения воспроизводимой величины сложнее, чем линейная, погрешность может быть указана в виде таблицы по выбранным диапазонам (в абсолютной или относительной форме) или в виде функции зависимости этой погрешности.
1.9. Определения нестандартизованных терминов, употребляемых в данном стандарте, приведены в справочном приложении 1.
Примеры формул для вычисления погрешностей приведены в справочном приложении 2. Обозначения погрешностей приведены в справочном приложении 3. Примеры вычисления погрешностей приведены в справочном приложении 4.
2. СПОСОБЫ ВЫРАЖЕНИЯ ПОГРЕШНОСТЕЙ ПЕРВИЧНЫХ ЭТАЛОНОВ
2.2. Случайная погрешность характеризуется средним квадратическим отклонением (СКО) результата измерений S при воспроизведении единицы (или при воспроизведении единицы и передаче ее размера) с указанием числа независимых наблюдений.
2.3. Нестабильность эталона v следует характеризовать изменением размера единицы за определенный промежуток времени, который указывается.
2.4. Погрешность передачи размера единицы характеризуют указанием среднего квадратического отклонения результата измерений SεΣ, обусловленного влиянием случайных и неисключенных систематических погрешностей метода и средств измерений, примененных при передаче размера единицы.
3. СПОСОБЫ ВЫРАЖЕНИЯ ПОГРЕШНОСТЕЙ ВТОРИЧНЫХ ЭТАЛОНОВ
3.1. Суммарная погрешность вторичного эталона характеризуется средним квадратическим отклонением результата измерений (SΣ) при его сличении с первичным эталоном или вышестоящим по поверочной схеме вторичным эталоном или же в виде доверительной границы погрешности tΣSΣ с доверительной вероятностью 0,99.
При учете неисключенной систематической погрешности через SΣ, следует выражать среднее квадратическое отклонение суммы неисключенных систематических и случайных погрешностей эталона.
Если неисключенную систематическую погрешность и нестабильность вторичного эталона указывают отдельно, то их выражают в виде, принятом для первичного эталона (пп. 2.1, 2.3).
ПРИЛОЖЕНИЕ 1
Справочное
ТЕРМИНЫ И ИХ ОПРЕДЕЛЕНИЯ
|
Термин |
Определение |
|
1. Размер единицы |
Размер физической величины, принятой за единицу |
|
2. Нестабильность эталона |
Изменение размера единицы, воспроизводимой или хранимой эталоном, в установленный промежуток времени |
|
3. Погрешность воспроизведения единицы |
Погрешность результата измерений, выполняемых при воспроизведении единицы |
|
4. Погрешность передачи размера единицы |
Погрешность результата измерений, выполняемых при передаче размера единицы |
|
5. Неисключенная систематическая погрешность |
Систематическая погрешность, оставшаяся после введения поправки |
|
6. Оценка погрешности средства измерений |
Погрешность данного средства измерений, полученная из ограниченного числа данных |
ПРИЛОЖЕНИЕ 2
Справочное
ПРИМЕРЫ ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ
Доверительную вероятность при определении доверительных границ погрешности эталона (как для случайной, так и для неисключенной систематической) принимают равной 0,99.
1. Границу неисключенной систематической погрешности эталона Θ вычисляют по формуле
При числе слагаемых N ≥ 4
где Θi - граница i-й составляющей неисключенной систематической погрешности эталона;
K - коэффициент зависимости неисключенных систематических погрешностей от выбранной доверительной вероятности при их равномерном распределении при доверительной вероятности 0,99 K = 1,4.
2. Среднее квадратическое отклонение результата прямых измерений с многократными наблюдениями S выражают по формуле
![]() (3)
(3)
где Si - среднее квадратическое отклонение результата наблюдений, вычисляемое по формуле
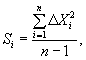 (4)
(4)
где
![]()
n - число наблюдений;
Xi - результат i-го наблюдения;
![]() - результат
измерений, вычисленный как среднее арифметическое результатов наблюдений.
- результат
измерений, вычисленный как среднее арифметическое результатов наблюдений.
Примечание. При многократных наблюдениях должна быть обеспечена практическая независимость отдельных наблюдений.
3. Среднее квадратическое отклонение результата косвенных измерений величины, являющейся функцией
X = F(Y1, Y2 … Ym)
вычисляют по формуле
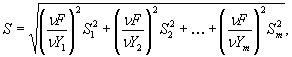 (5)
(5)
где S1, S2, … Sm - средние квадратические отклонения результатов измерений величин Y1, Y2, … Ym.
4. Границу неисключенной систематической погрешности при косвенном измерении в зависимости от числа слагаемых вычисляют по формулам (1) или (2), в которых
![]() (6)
(6)
где ∆Yi - неисключенная систематическая погрешность измерения величины Yi.
5. Среднее квадратическое отклонение суммы неисключенных систематических и случайных погрешностей SΣ вычисляют по формуле
где ![]() - среднее квадратическое отклонение суммы неисключенных систематических погрешностей.
- среднее квадратическое отклонение суммы неисключенных систематических погрешностей.
6. При определении доверительной границы погрешности tΣSΣ вторичного эталона коэффициент tΣ вычисляют по формуле
где ![]() - коэффициент для нахождения доверительных границ погрешности результата измерений.
- коэффициент для нахождения доверительных границ погрешности результата измерений.
7. Погрешность передачи размера единицы состоит из суммы случайных и неисключенных систематических погрешностей метода и средств измерений, применяемых для передачи размера единицы. Оценку суммы неисключенных систематических и случайных погрешностей указывают в виде среднего квадратического отклонения SεΣ, которое вычисляют по формуле
![]() (9)
(9)
где Sε - среднее квадратическое отклонение случайной погрешности метода и средства передачи размера единицы;
![]() -
среднее
квадратическое отклонение неисключенной систематической погрешности
метода и средств передачи размера единицы.
-
среднее
квадратическое отклонение неисключенной систематической погрешности
метода и средств передачи размера единицы.
ПРИЛОЖЕНИЕ 3
Справочное
ОБОЗНАЧЕНИЯ
Θi, Θi0 - граница i-й составляющей неисключенной систематической погрешности эталона в абсолютной и относительной форме
Θ, Θ0 - граница неисключенной систематической погрешности эталона в абсолютной и относительной форме
Хi - результат i-го наблюдения
![]() - результат
измерений
- результат
измерений
Si, Si0 - среднее квадратическое отклонение i-го результата наблюдения в абсолютной и относительной форме
S, S0 - среднее квадратическое отклонение результата измерения в абсолютной и относительной форме
SΘ - среднее квадратическое отклонение суммы неисключенных систематических погрешностей, рассматриваемых как случайные величины
SΣ - среднее квадратическое отклонение суммы случайных погрешностей (или суммы случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины)
![]() - коэффициент для
нахождения доверительных границ погрешности результата измерения
- коэффициент для
нахождения доверительных границ погрешности результата измерения
![]() - доверительная
граница случайной погрешности результата измерений
- доверительная
граница случайной погрешности результата измерений
tΣ - коэффициент для нахождения доверительных границ суммы случайных погрешностей и неисключенных систематических погрешностей
tΣ·SΣ - доверительная граница суммы случайных погрешностей (или суммы случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины)
K - коэффициент для нахождения границ неисключенных систематических погрешностей
v - нестабильность эталона
SεΣ - среднее квадратическое отклонение результата измерений при передаче размера единицы от первичного эталона вторичному эталону
Sε - среднее квадратическое отклонение случайной погрешности средства и метода передачи размера единицы
Θε - граница неисключенной систематической погрешности средства и метода передачи размера единицы
Р - доверительная вероятность
ПРИЛОЖЕНИЕ 4
Справочное
ПРИМЕР ВЫЧИСЛЕНИЯ ПОГРЕШНОСТЕЙ
Погрешности рабочего эталона единицы длины - штрихового метра при сличении с первичным эталоном интерференционным методом определены на основании десяти наблюдений (n = 10):
1. Результат измерений ![]() = 1 м
+ 1,47 мкм.
= 1 м
+ 1,47 мкм.
2. Среднее квадратическое отклонение результата измерений при - сличении рабочего эталона с первичным S = 0,023 мкм.
Вычислены неисключенные систематические погрешности:
из-за неточного определения показателя преломления воздуха Θ1 = 0,030 мкм
из-за неточного значения длин волн Θ2 = 0,016 мкм
из-за неточного значения температуры Θ3 = 0,026 мкм
из-за неточного определения поправок на размер
коллиматорной щели Θ4 = 0,002 мкм
Требуется определить доверительные границы суммарной погрешности рабочего эталона.
Решение: 1. По формуле (2) определяют границы неисключенных систематических погрешностей
![]()
Θ = 0,06 мкм; Р = 0,99. Принимается, что составляющие имеют равномерное распределение N = 4.
2. По формуле (7) вычисляют среднее квадратическое отклонение суммы неисключенных систематических и случайных погрешностей SΣ
![]()
3. Вычисляют доверительные границы суммарной погрешности tΣSΣ, полагая распределение случайных погрешностей нормальным. Для этого предварительно вычисляют коэффициент tΣ по
формуле (8), выбрав из таблиц Стьюдента ![]() = 3,25 (Р = 0,99; n = 10):
= 3,25 (Р = 0,99; n = 10):
![]()
Доверительные границы суммарной погрешности:
tΣSΣ = ±2,81·0,034 мкм = ±0,096 мкм ≈ ±0,10 мкм.
4. Из исследований платино-иридиевой штриховой меры (рабочий эталон) за ряд лет установлено, что его максимальная нестабильность не превышает 0,10 мкм в год, т.е. v = 0,10 мкм/год.
Следовательно, результат измерений, полученный из 10 наблюдений, равен 1 м + 1,47 мкм. При этом суммарная погрешность, состоящая из неисключенных систематических погрешностей при равномерном распределении и случайной погрешности при нормальном распределении и доверительной вероятности 0,99, составляет ±0,10 мкм.
Форма представления результата может быть следующей:
![]() = 1 м
+ 1,47 мкм;
= 1 м
+ 1,47 мкм;
tΣ·SΣ = ±0,10 мкм нормальной n = 10 и равномерном распределении
при Р = 0,99, N = 4
и равномерном распределении N = 4.
Нестабильность эталона v = 0,10 мкм/год.
ПРИЛОЖЕНИЕ 5
Справочное
ИНФОРМАЦИОННЫЕ ДАННЫЕ О СООТВЕТСТВИИ
ГОСТ 8.381-80 и СТ СЭВ 403-76
1. Разд. 1, 2, 3 ГОСТ 8.381-80 соответствуют разд. 1, 2, 3 СТ СЭВ 403-76.
2. Справочное приложение 1 ГОСТ 8.381-80 соответствует пп. 6, 8, 9 информационного приложения 1 СТ СЭВ 403-76.
3. Справочные приложения 2, 3, 4 ГОСТ 8.381-80 соответствуют информационным приложениям 2, 3, 4 СТ СЭВ 403-76.
СОДЕРЖАНИЕ
