РАГС - РОССИЙСКИЙ АРХИВ ГОСУДАРСТВЕННЫХ СТАНДАРТОВ, а также строительных норм и правил (СНиП)
и образцов юридических документов
Произвольная ссылка:
ГОСТ ИСО 11453-2005 Статистические методы. Статистическое представление данных. Проверка гипотез и доверительные интервалы для пропорций.
|
МЕЖГОСУДАРСТВЕННЫЙ СОВЕТ ПО СТАНДАРТИЗАЦИИ, МЕТРОЛОГИИ И
СЕРТИФИКАЦИИ INTERSTATE COUNCIL FOR
STANDARDIZATION, METROLOGY AND CERTIFICATION |
|
|
МЕЖГОСУДАРСТВЕННЫЙ |
ГОСТ ИСО |
Статистические методы
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
Проверка гипотез и доверительные интервалы для пропорций
ISO 11453:1996
Statistical interpretation of data -
Tests and confidence intervals relating to proportions
(IDT)
|
|
Москва |
Содержание
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-97 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила, рекомендации по межгосударственной стандартизации. Порядок разработки, принятия, применения, обновления и отмены»
Сведения о стандарте
1 РАЗРАБОТАН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО НИЦКД), Межгосударственным техническим комитетом по стандартизации МТК 125 «Статистические методы в управлении качеством продукции»
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии Российской Федерации
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол № 28 от 9 декабря 2005 г.)
За принятие проголосовали:
|
Краткое наименование страны по МК (ИСО 3166) 004-97 |
Код страны по МК (ИСО 3166) 004-97 |
Сокращенное наименование национального органа по стандартизации |
|
Азербайджан |
AZ |
Азстандарт |
|
Армения |
AM |
Армстандарт |
|
Беларусь |
BY |
Госстандарт Республики Беларусь |
|
Казахстан |
KZ |
Госстандарт Республики Казахстан |
|
Кыргызстан |
KG |
Кыргызстандарт |
|
Молдова |
MD |
Молдова-Стандарт |
|
Российская Федерация |
RU |
Федеральное агентство по техническому регулированию и метрологии |
|
Таджикистан |
TJ |
Таджикстандарт |
|
Туркменистан |
TM |
Главгосслужба «Туркменстандартлары» |
|
Узбекистан |
UZ |
Узстандарт |
|
Украина |
UA |
Госпотребстандарт Украины |
4 Настоящий стандарт идентичен международному стандарту ИСО 11453:1996 «Статистическое представление данных. Проверка гипотез и доверительные интервалы для пропорций» (ISО 11453:1996 «Statistical interpretation of data - Tests and confidence intervals relating to proportions»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ 1.5.
Степень соответствия - идентичная (IDТ).
5 Приказом Федерального агентства по техническому регулированию и метрологии от 29 июня 2006 г. № 125-ст межгосударственный стандарт ГОСТ ИСО 11453-2005 введен в действие с 1 сентября 2006 г.
6 ВВЕДЕН ВПЕРВЫЕ
Информация о введении в действие (прекращении действия) настоящего стандарта публикуется в указателе «Национальные стандарты».
Информация об изменениях к настоящему стандарту публикуется в указателе (каталоге) «Национальные стандарты», а текст изменений - в информационных указателях «Национальные стандарты». В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в информационном указателе «Национальные стандарты»
ГОСТ ИСО 11453-2005
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
Статистические методы
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ Проверка гипотез и доверительные интервалы для пропорций
Statistical methods. Statistical interpretation
of data.
Tests and confidence intervals relating to proportions
Дата введения - 2006-09-01
1 Область применения
Настоящий стандарт содержит описание статистических методов, предназначенных для решения следующих задач:
a) Дана совокупность элементов, из которых отобрана выборка из п элементов, и у х элементов выборки обнаружена некоторая характеристика. Какая доля (пропорция) совокупности имеет эту характеристику (см. 8.1)?
b) Отличается ли пропорция, определенная в соответствии с задачей а), от номинального указанного значения (см. 8.2)?
c) Даны две различные совокупности. Различаются ли доли элементов с заданной характеристикой в этих двух совокупностях (см. 8.3)?
d) Выборки какого объема следует отбирать для решения задач b) и с), чтобы быть достаточно уверенным в правильности решения (см. 7.2.3 и 7.3.3)?
Важно, чтобы метод отбора выборок не оказывал заметного влияния на совокупность. Если взятая случайным образом выборка составляет менее 10 % совокупности, как правило, это является приемлемым. Если выборка составляет более 10 % совокупности, надежные результаты можно получить только возвращая каждый отобранный элемент перед отбором следующего элемента.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ИСО 3534.1:1993 Статистика. Словарь и условные обозначения. Часть 1: Вероятность и основы статистики
3 Определения
В настоящем стандарте применены термины по ИСО 3534.1, а также следующий термин с соответствующим определением:
3.1 целевой элемент (target item): Элемент, в котором обнаружена указанная характеристика.
4 Символы
В настоящем стандарте использованы следующие символы:
a - выбранный уровень значимости;
a' - достигнутый уровень значимости;
(1 - a) - выбранный уровень доверия;
b - вероятность ошибки второго вида;
п; п1; п2 - объем выборки; объем выборки 1; объем выборки 2;
X - число целевых элементов в выборке (случайная величина);
х - значение X;
р - доля (пропорция) целевых элементов совокупности;
pи, 0 - верхняя граница одностороннего доверительного интервала для р;
pl, 0 - нижняя граница одностороннего доверительного интервала для р;
pи, t - верхняя граница двустороннего доверительного интервала для р;
pl, t - нижняя граница двустороннего доверительного интервала для р;
Т - значение, используемое для определения доверительных границ;
Сl, 0 - критическое значение при проверке нулевой гипотезы H0: р ³ р0;
Си,0 - критическое значение при проверке нулевой гипотезы H0: р £ р0;
Cl, t - нижняя граница критической области при проверке нулевой гипотезы Но: р = р0;
Си,t - верхняя граница критической области при проверке нулевой гипотезы Но: р = р0;
р0 - заданное значение для р;
р' - значение р, для которого определяется вероятность неотклонения нулевой гипотезы Pa;
Pa - вероятность неотклонения нулевой гипотезы;
f1, f2 - числа степеней свободы F-распределения;
F1, F2 - тестовые статистики;
Fq (f1, f2) - квантиль уровня q F-распределения с f1 и f2 степенями свободы;
z1, z2 - тестовые статистики;
uq - квантиль уровня q стандартного нормального распределения;
q, h, K - вспомогательные величины.
5 Точечная оценка пропорции р
Оценку р по выборке из п элементов с х целевыми элементами определяют по формуле
![]()
Эта оценка является несмещенной, если выборка отбиралась случайным образом, независимо от объема выборки и размера совокупности, даже если выборка составляет заметную часть совокупности.
6 Доверительные границы для пропорции р
Процедуры определения границ доверительного интервала для р приведены в 8.1 (формы А-1 - А-3).
Границы доверительного интервала зависят от объема выборки п, числа целевых элементов в выборке х и выбранного уровня доверия (1 - a). Невозможно точно достичь заданного уровня доверия из-за дискретности х. Приведенная в стандарте процедура дает минимальное значение уровня доверия, не превосходящее (1 - a).
В настоящем стандарте при определении границ двустороннего доверительного интервала для заданного уровня доверия (1 - a) используется процедура определения нижних границ одностороннего доверительного интервала для уровня доверия (1 - a/2). Это гарантирует, что вероятность ошибки меньше или равна a/2 с каждой стороны интервала.
7 Проверка гипотез для пропорции р
7.1 Общие требования
Для решения практических задач в формах В-1 - В-3 (8.2) и С-1 - С-3 (8.3) приведены нулевые гипотезы для пропорций и схемы их проверки. Сначала должны быть выбраны соответствующая нулевая гипотеза, объем выборки п (объемы выборок п1 и п2) и уровень значимости. Поскольку основные используемые распределения дискретны, процедуры разработаны так, чтобы достичь самого близкого к выбранному значению уровня значимости, который меньше или равен этому значению. В формах не приведены альтернативные гипотезы, так как в каждом случае неявно предполагается, что альтернативная гипотеза является дополнительной к нулевой гипотезе.
Пример - При работе с формами В (процедура сравнения пропорции с заданным значением) вначале необходимо выбрать одну из следующих трех нулевых гипотез Н0 (с дополнительной альтернативной гипотезой Н1), где р0 - заданное значение:
a) односторонний критерий с Н0: р ³ р0 и Н1: р < р0;
b) односторонний критерий с Н0: р £ р0 и Н1: р > р0;
c) двусторонний критерий с Н0: р = р0 и Н1: р ¹ р0;
Результатом проверки гипотезы является отклонение или неотклонение нулевой гипотезы.
Отклонение нулевой гипотезы означает, что принимается альтернативная гипотеза. Неотклонение нулевой гипотезы не означает, что принимается нулевая гипотеза (см. 7.2.2).
7.2 Сравнение пропорции с заданным значением р0
7.2.1 Процедура проверки гипотез
Процедуры проверки нулевых гипотез:
Н0: р ³ р0;
Н0: р £ р0;
Н0: р = р0.
где р0 - заданное значение; описаны в формах В-1 - В-3. Эти процедуры особенно просты для применения, если известны критические значения для заданных значений п, р и a. Если критические значения неизвестны, их можно определить при выполнении процедуры в соответствии с формами В (8.2).
7.2.2 Оперативные характеристики
Вычисление оперативных характеристик (включая вероятность ошибки первого рода, достигнутого уровня значимости и вероятности ошибки второго рода) описано в приложении А. Для вычисления этих характеристик критические значения должны быть известны (см. 7.2.1) и должна быть выбрана альтернативная гипотеза р = р1, для которой определяется вероятность ошибки второго рода.
7.2.3 Определение объема выборки п
Если объем выборки не определен (например, по экономическим или техническим причинам), его минимальное значение должно быть задано таким, чтобы для выбранной нулевой гипотезы Н0 (см. 7.2.1) достигнутое значение уровня значимости не превосходило выбранного или заданного значения. Кроме того, достигнутое значение ошибки второго рода (вероятность β) должно быть приблизительно равно выбранному или заданному значению β, если р равно выбранному значению р'. Для этой цели р0 и р' должны быть отмечены на шкале р, а α, (1 - α), α/2, (1 - α/2) - на шкале Р и прямых линиях 1 и 2 в соответствии с таблицей 1 и номограммой Ларсона (рисунок 2).
Таблица 1 - Процедура определения объема выборок по номограмме Ларсона (рисунок 2)
|
Нулевая гипотеза |
Заданное значение |
Прямая линия 1 из точки р0 в точку |
Прямая линия 2 из точки р' в точку |
|
Н0: р ³ р0; |
р' < р0 |
α |
1 - β |
|
Н0: р £ р0; |
р' > р0 |
1 - α |
β |
|
Н0: р = р0. |
р' > р0 |
1 - α/2 |
β |
|
Н0: р = р0. |
р' < р0 |
α/2 |
1 - β |
Точка пересечения прямых линий 1 и 2, указанных в таблице 1, дает значения Сl, 0 (Cu, 0) на шкале х. Если х - не целое число, его следует округлить до ближайшего целого числа.
7.3 Сравнение двух пропорций
7.3.1 Процедура проверки гипотез
Процедуры проверки для нулевых гипотез:
Н0: р1 ³ р2;
Н0: р1 £ р2;
Н0: р1 = р2.
где р1 - доля (пропорция) целевых элементов в совокупности 1, а р2 - доля (пропорция) целевых элементов в совокупности 2, описаны в формах С-1 - С-3 (8.3). Эти процедуры можно использовать для анализа независимости двух атрибутов (дихотомических характеристик) элементов совокупности.
7.3.2 Оперативные характеристики
Предположения:
a) для одностороннего критерия Н0: р1 £ р2 мощность (1 - β) определяют для заданной пары пропорций р1 и р2, где р1 > р2;
b) для проверки гипотез используют две выборки одного и того же объема, то есть n1 = n2 = n.
Если α - уровень значимости, то достаточно точное приближенное значение мощности может быть получено обратным преобразованием по [1]:
1 - β = Φ(z - u1-α)
где Φ - функция распределения стандартного нормального распределения;
u1-α - квантиль стандартного нормального распределения уровня (1 - α);
![]()
Это приближение может также использоваться и для двустороннего критерия Н0: р1 = р2 с альтернативной гипотезой Н1: р1 > р2, если α заменить в формуле на α/2.
7.3.3 Определение объема выборки п
Если объемы выборок n1 и n2 не заданы, их минимальные значения должны быть выбраны такими, чтобы мощность критерия была не менее (1 - β), а уровень значимости - не менее α.
Предполагается, что нулевая гипотеза является односторонней Н0: р1 £ р2. Однако приведенные процедуры применимы также для двустороннего критерия Н0: р1 = р2 с альтернативной гипотезой Н0: р1 > р2, если заменить α на α/2.
Точные значения объема выборок приведены в таблицах 5 и 6 и в [2] для выбранных значений α и β. Эти таблицы предполагают, что объемы выборок равны, т.е. n = n1 = n2.
Для сочетаний α, р1, р2 и (1 - β), не приведенных в таблицах 5 и 6, может использоваться следующее приближение, которое учитывает неравные объемы выборок, однако необходимо, чтобы отношение r объемов выборок было выбрано заранее.
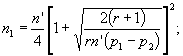
n2 = n1/r;

![]()
![]()
8 Формы
Для простоты применения форм необходимо отметить квадратики, представляющие активизированную часть формы, а затем выполнить необходимые действия, вводя необходимые данные.
8.1 Формы А. Доверительный интервал для пропорции р
8.1.1 Форма А-1 - Односторонний доверительный интервал с верхней границей для пропорции р
|
Характеристика: |
|||||
|
Процедура определения: |
|||||
|
Элементы: |
|||||
|
Критерий для идентификации целевых элементов: |
|||||
|
Примечания: |
|||||
|
Выбранный уровень доверия 1 - α = |
|||||
|
Объем выборки п = |
|||||
|
Число целевых элементов в выборке х = |
|||||
|
Определение границы доверительного интервала |
|||||
|
а) Процедура для п ≤ 30 £ |
|||||
|
1) Случай х = п £ |
|||||
|
pи,0 = 1 |
|||||
|
2) Случай х < п £ |
|||||
|
По таблице 2 для известных значений п, X = х и q = (1 - α) определяют |
|||||
|
pи,0 = T1-α (n, x) = |
|||||
|
b) Процедура для п > 30 £ |
|||||
|
1) Случай х = 0 £ |
|||||
|
pи,0 = 1 - α1/n = |
|||||
|
2) Случай х = п £ |
|||||
|
pи,0 = 1 |
|||||
|
3) Случай 0 < х < п £ |
|||||
|
По таблице 3 для q = (1 - α) определяют u1-α = |
|||||
|
Значение d, соответствующее выбранному уровню доверия, определяют по следующей таблице. |
|||||
|
|
1 - α |
0,90 |
0,95 |
0,99 |
|
|
|
d |
0,411 |
0,677 |
1,353 |
|
|
|
|||||
|
где р* = (х + 1)/(n + 1). |
|||||
|
Результат (искомый доверительный интервал): |
|||||
|
р £ pи,0 = |
|||||
8.1.2 Форма А-2. Односторонний доверительный интервал с нижней границей для пропорции р
|
Характеристика: |
|||||
|
Процедура определения: |
|||||
|
Элементы: |
|||||
|
Критерий для идентификации целевых элементов: |
|||||
|
Примечания: |
|||||
|
Выбранный уровень доверия 1 - α = |
|||||
|
Объем выборки п = |
|||||
|
Число целевых элементов в выборке х = |
|||||
|
Определение границы доверительного интервала |
|||||
|
а) Процедура для п ≤ 30 £ |
|||||
|
1) Случай х = 0 £ |
|||||
|
pl,0 = 0 |
|||||
|
2) Случай х > 0 £ |
|||||
|
По таблице 2 для известных значений п, Х= п - х и q = (1 - α) определяют: |
|||||
|
T1-α (n, n - x) = |
|||||
|
pl,0 = 1- T1-α (n, n - x) = |
|||||
|
b) Процедура для п > 30 £ |
|||||
|
1) Случай х = 0 £ |
|||||
|
pl,0 = 0 |
|||||
|
2) Случай х = п £ |
|||||
|
pl,0 = α1/n = |
|||||
|
3) Случай 0 < х < п £ |
|||||
|
По таблице 3 для q = 1 - α определяют u1-α = |
|||||
|
Значение d, соответствующее выбранному уровню доверия, определяют по следующей таблице. |
|||||
|
|
1 - α |
0,90 |
0,95 |
0,99 |
|
|
|
d |
0,411 |
0,677 |
1,353 |
|
|
|
|||||
|
где р* = х/(n + 1). |
|||||
|
Результат (искомый доверительный интервал): |
|||||
|
р £ pl,0 = |
|||||
8.1.3 Форма А-3. Двусторонний доверительный интервал для пропорции р
|
Характеристика: |
||||||||||
|
Процедура определения: |
||||||||||
|
Элементы: |
||||||||||
|
Критерий для идентификации целевых элементов: |
||||||||||
|
Примечания: |
||||||||||
|
Выбранный уровень доверия 1 - α = |
||||||||||
|
Объем выборки п = |
||||||||||
|
Число целевых элементов в выборке х = |
||||||||||
|
Определение границ доверительного интервала |
||||||||||
|
а) Процедура для п ≤ 30 £ |
||||||||||
|
1) Определение верхней границы доверительного интервала: |
||||||||||
|
- Случай х = п £ |
||||||||||
|
pи,t = 1 |
||||||||||
|
- Случай х < п £ |
||||||||||
|
По таблице 2 для известных значений п, Х= п - х и q = (1 – α/2) определяют: |
||||||||||
|
pи,t = T1-α/2 (n, x) = |
||||||||||
|
2) Определение нижней границы доверительного интервала: |
||||||||||
|
- Случай х = 0 £ |
||||||||||
|
- Случай х > 0 £ |
||||||||||
|
По таблице 2 для известных значений п, Х= п - х и q = (1 – α/2) определяют: |
||||||||||
|
T1-α/2 (n, n - x) = |
||||||||||
|
pl,t = 1- T1-α/2 (n, n - x) = |
||||||||||
|
b) Процедура для п > 30 £ |
||||||||||
|
1) Определение верхней границы доверительного интервала: |
||||||||||
|
- Случай х = 0 £ |
||||||||||
|
pи,t = 1 - (α/2)1/n = |
||||||||||
|
- Случай х = п £ |
||||||||||
|
pи,t = 1 |
||||||||||
|
- Случай 0 < х < п £ |
||||||||||
|
По таблице 3 для q = (1 - α/2) определяют u1- α/2 = |
||||||||||
|
Значение d, соответствующее выбранному уровню доверия, определяют по следующей таблице. |
||||||||||
|
|
1 - α |
0,90 |
0,95 |
0,99 |
|
|||||
|
|
d |
0,677 |
0,960 |
1,659 |
|
|||||
|
|
||||||||||
|
где р* = (х + 1)/(n + 1). |
||||||||||
|
2) Определение нижней границы доверительного интервала: |
||||||||||
|
- Случай х = 0 £ |
||||||||||
|
pl,t = 0 |
||||||||||
|
- Случай х = п £ |
||||||||||
|
pl,t = (α/2)1/n = |
||||||||||
|
- Случай 0 < х < п £ |
||||||||||
|
По таблице 3 для q = (1 - α/2) определяют u1- α/2 = |
||||||||||
|
Значение d, соответствующее выбранному уровню доверия, определяют по следующей таблице. |
||||||||||
|
|
1 - α |
0,90 |
0,95 |
0,99 |
|
|||||
|
|
d |
0,677 |
0,960 |
1,659 |
|
|||||
|
|
||||||||||
|
где р* = х/(n + 1). |
||||||||||
|
Результаты (искомый доверительный интервал): pl, t = pu,t = pl, t ≤ p ≤ pu,t |
||||||||||
8.2 Формы В. Сравнение пропорции р с заданным значением р0
8.2.1 Форма В-1. Сравнение пропорции р с заданным значением р0 для одностороннего критерия Н0: р ³ р0
|
Характеристика: Процедура определения: Элементы: Критерий для идентификации целевых элементов: Примечания: |
|
Данное значение р0 = Выбранный уровень значимости α = Объем выборки п = Число целевых элементов в выборке х = |
|
Процедура проверки гипотез |
|
I Критические значения известны (см. 7.2.1) £ Cl, 0 = Гипотезу Н0 отклоняют, если х < Cl, 0; в противном случае гипотезу не отклоняют. |
|
II Критические значения неизвестны £ |
|
а) Случай х ≥ р0п £ Гипотезу Н0 не отклоняют |
|
b) Случай х < р0п £ |
|
1) Процедура для п ≤ 30 £ |
|
По 8.1.1 (форма А-1) определяют одностороннюю верхнюю доверительную границу для п, х и уровня доверия (1 - α) pи,0 = Гипотезу Н0 отклоняют, если pи,0 < р0, в противном случае гипотезу не отклоняют. |
|
2) Процедура для п > 30 £ |
|
- Случай х = 0 £ |
|
pи,0 = 1 - α1/n = [см. 8.1.1 в) 1)]. |
|
Гипотезу Н0 отклоняют, если pи,0 < р0 , в противном случае гипотезу не отклоняют. |
|
- Случай 0 < х < £ |
|
По таблице 3 для q = (1 - α) определяют u1- α = |
|
|
|
Гипотезу Н0 отклоняют, если u1 > u1- α в противном случае гипотезу не отклоняют. |
|
Результат проверки гипотезы: |
|
Гипотеза Н0 отклонена £ |
|
Гипотеза Н0 не отклонена £ |
|
Определение критических значений Cl, 0 - наименьшее неотрицательное целое число х, для которого процедура проверки гипотез по форме В-1(II) не ведет к отклонению гипотезы Н0. Значение Cl, 0 определяют методом итераций путем повторного применения формы В-1 (II) с различными значениями х, пока не будут найдены такие два значения х, которые отличаются друг от друга на 1, и при этом одно из значений приводит к отклонению нулевой гипотезы Н0, а другое значение приводит к неотклонению нулевой гипотезы Н01). Начальное значение хстарт может быть получено следующим образом. |
|
В качестве х*2) принимают значение пр0, округленное до ближайшего целого числа pl,0|x = x* = (pl,0|x = x* определяют по 8.1.2, форма А-2) хстарт = значение npl,0|x = x*, округленное до ближайшего целого числа = |
|
Интерпретация результатов проверки гипотез по форме В-1 (II): для х £ Cl, 0 - 1 = гипотезу Н0 отклоняют; для х ³ Cl, 0 = гипотезу Н0 отклоняют. |
|
Результат: Cl, 0 = |
|
1) Критическое значение (или одно из критических значений) может не существовать для некоторых значений р0 и/или для очень маленьких объемов выборок п. |
|
2) х* - вспомогательная величина для нахождения хстарт |
8.2.2 Форма В-2. Сравнение пропорции р с заданным значением р0 для одностороннего критерия с Н0: р £ р0
|
Характеристика: Процедура определения: Элементы: Критерий для идентификации целевых элементов: Примечания: |
|
Заданное значение р0 = Выбранный уровень значимости a = Объем выборки п = Число целевых элементов в выборке х = |
|
Процедура проверки гипотез |
|
I Критические значения известны (см. 7.2.1) Си,0 = Гипотезу Н0 отклоняют, если х > Си,0, в противном случае гипотезу не отклоняют. |
|
II Критические значения неизвестны £ |
|
а) Случай х £ роп £ |
|
Гипотезу Н0 не отклоняют. |
|
b) Случай х > р0п £ |
|
1) Процедура для п £ 30 £ |
|
По 8.1.2 (форма А-2) определяют одностороннюю нижнюю доверительную границу для п, х и уровня доверия (1 - a) |
|
pl, 0 = |
|
Гипотезу Н0 отклоняют, если pl, 0 > р0, в противном случае гипотезу не отклоняют. |
|
2) Процедура для п > 30 £ |
|
- Случай х = п £ |
|
pl, 0 = a1/n = [см. 8.1.2 b) 2)]. |
|
Гипотезу Н0 отклоняют, если pl, 0 > р0, в противном случае гипотезу не отклоняют. |
|
- Случай 0 < х < п £ |
|
По таблице 3 для q = (1 - a) определяют u1- α = |
|
|
|
Гипотезу Н0 отклоняют, если и2 > u1- α, в противном случае гипотезу не отклоняют. |
|
Результат проверки гипотезы: |
|
Гипотеза Н0 отклонена £ |
|
Гипотеза Н0 не отклонена £ |
|
Определение критических значений |
|
Си,0 - наибольшее целое число х, для которого процедура проверки гипотез по форме В-2 (II) не ведет к отклонению нулевой гипотезы. Значение Си,0 определяют методом итераций путем повторного применения формы В-2 (II) с различными значениями х, пока не будут найдены такие два значения, которые отличаются друг от друга на 1, и при этом одно из значений приводит к отклонению нулевой гипотезы Н0, а другое значение приводит к неотклонению нулевой гипотезы Н01). Начальное значение хстарт может быть получено следующим образом. |
|
В качестве х*2) принимают значение пр0, округленное до ближайшего целого числа pu,0|x = x* = (pu,0|x = x* определяют по 8.1.1, форма А-1) хстарт = значение npu,0|x = x*, округленное до ближайшего целого числа = |
|
Интерпретация результатов проверки гипотез по форме В-2 (II): |
|
для х £ Си,0 = гипотезу Н0 не отклоняют; |
|
для х ³ Си,0 + 1 = гипотезу Н0 отклоняют. |
|
Результат: |
|
Си,0 = |
|
1) Критическое значение (или одно из критических значений) может не существовать для некоторых значений р0 и/или для очень маленьких объемов выборок п. |
|
2) х* - вспомогательная величина для нахождения хстарт |
8.2.3 Форма В-3. Сравнение пропорции р с данным значением р0 для двустороннего критерия Н0: р = р0
|
Характеристика: Процедура определения: Элементы: Критерий для идентификации целевых элементов: Примечания: |
|
Заданное значение р0 = Выбранный уровень значимости a = Объем выборки п = Число целевых элементов в выборке х = |
|
Процедура проверки гипотез |
|
I Критические значения известны (см. 7.2.1) £ Cl,t = Cu,t = Гипотезу Н0 отклоняют, если х < Cl,t или х > Cu,t, в противном случае гипотезу не отклоняют. |
|
II Критические значения неизвестны |
|
а) Процедура для п £ 30 £ |
|
По 8.1.3 (форма А-3) определяют двусторонние доверительные границы для п, х и уровня доверия (1 - a): pl,t = pu,t = Гипотезу Н0 отклоняют, если pl,t > р0 или pu,t < р0, в противном случае гипотезу не отклоняют. |
|
b) Процедура для п > 30 £ |
|
1) Случай х = 0 £ pu,t = 1 - (a/2)1/n = Гипотезу Н0 отклоняют, если pu,t < р0, в противном случае гипотезу не отклоняют. |
|
2) Случай х = п £ pl,t = (a/2)1/n = Гипотезу Н0 отклоняют, если pl,t > р0, в противном случае гипотезу не отклоняют. |
|
3) Случай 0 < х < п £ По таблице 3 для q = (1 - α/2) определяют u1- α/2 =
|
|
Гипотезу Н0 отклоняют, если u1 > u1- α/2 или u2 > u1- α/2 в противном случае гипотезу не отклоняют. |
|
Результат проверки гипотез: |
|
Гипотеза Н0 отклонена £ |
|
Гипотеза Н0 не отклонена £ |
|
Определение критических значений Cl,t - наименьшее неотрицательное целое число х, а Си,t - наибольшее целое число х, для которого проверка гипотез по форме В-3 (II) не ведет к отклонению Н0. Значения Cl,t и Си,t определяют методом итераций путем повторного применения формы В-3 (II) с различными значениями х до тех пор, пока не будут определены такие две пары значений, у которых значения в каждой паре отличаются друг от друга на 1, и при этом одно из значений приводит к отклонению нулевой гипотезы Н0, а другое значение приводит к неотклонению нулевой гипотезы Н01). Начальное значение хстарт может быть получено следующим образом. |
|
В качестве х*2) определяют значение пр0, округленное до ближайшего целого числа. pi,t|x = x* = pu,t|x = x* = pi,t|x = x* и pu,t|x = x* определяют по 8.1.3 (форма А-3); хстарт (нижнее) = значение npi,t|x = x*, округленное до ближайшего целого числа, = хстарт (верхнее) = значение пpu,t|x = x*, округленное до ближайшего целого числа, = |
|
Интерпретация результатов проверки гипотез по форме В-3 (II): для х £ Cl,t - 1 = гипотезу Н0 отклоняют; для х = Cl,t = и х = Си,t = гипотезу Н0 не отклоняют; для х ³ Си t + 1 = гипотезу Н0 отклоняют. |
|
Результаты проверки гипотез: Cl,t = ; Си,t = |
|
1) Критическое значение (или одно из критических значений) может не существовать для некоторых значений р0 и/или для очень маленьких объемов выборок п. |
|
2) х* - вспомогательная величина для нахождения хстарт |
8.3 Формы С. Сравнение двух пропорций
8.3.1 Форма С-1. Сравнение двух пропорций для одностороннего критерия Н0: р1 ³ р2
|
Характеристика: Процедура определения: Элементы: Критерий для идентификации целевых элементов: Примечания: |
|
Выбранный уровень значимости a = Объем выборки 1: п1 = Объем выборки 2: п2 = Число целевых элементов в выборке 1: х1 = Число целевых элементов в выборке 2: х2 = |
|
Проверка для тривиального случая |
|
|
|
Неравенство является истинным £ |
|
Неравенство не является истинным £ |
|
Если неравенство является истинным, нулевую гипотезу не отклоняют и результат проверки гипотез может быть объявлен немедленно. В противном случае проводят следующую процедуру, которая может привести к отклонению или к неотклонению гипотезы Н0. |
|
Процедура проверки гипотез для нетривиальных случаев Если, по крайней мере, одно из четырех значений п1, п2, (х1 + х2), (п1 + п2 - х1 - х2) меньше или равно (п1 + п2)/4, то применяют биномиальную аппроксимацию, приведенную в I настоящей формы; в противном случае применяют нормальную аппроксимацию, приведенную в II настоящей формы. Однако даже если вышеупомянутое условие выполнено, можно применять нормальную аппроксимацию, если выполнены два следующих условия: - при применении биномиальной аппроксимации в таблице 4 F-распределения необходимо использовать интерполяцию; - п1 и п2 или (х1 + х2) и (п1 + п2 - х1 - х2) попарно являются величинами одного порядка. |
|
Решение: |
|
Должна применяться биномиальная аппроксимация (продолжить с I) £ |
|
Должна применяться нормальная аппроксимация (продолжить с II) £ |
|
I Биномиальная аппроксимация |
|
Определение величин: К1, К2, h1, h2 |
|
Если [п2 < п1 и п2 < (х1 + х2)] или [(п1 + п2 - х1 - х2) < п1 и (п1 + п2 - х1 - х2) < (х1 + х2)], искомые величины определяют следующим образом: |
|
h1 = п2 = |
|
h2 = п1 = |
|
К1 = п2 - х2 = |
|
К2 = п1 - х1 = |
|
В противном случае: |
|
h1 = п1 = |
|
h2 = п2 = |
|
К1 = х1 = |
|
К2 = х2 = |
|
Вычисление статистики и определение значений по таблице 4 |
|
а) Случай h1 £ К1+ К2 £ |
|
|
|
Числа степеней свободы F-распределения: |
|
f1 = 2(К1 + 1) = |
|
f2 = 2(h1 - К1) = |
|
По таблице 4 для q = (1 - a), f1 и f2 (при необходимости применяют интерполяцию) определяют: |
|
F1 - a( f1, f2) = |
|
b) Случай h1 > К1+ К2 |
|
|
|
Число степеней свободы F-распределения: |
|
f1 = 2(К1 + 1) = |
|
f2 = 2К2 = |
|
По таблице 4 для q = (1 - a), f1 и f2 определяют F1 - a( f1, f2) = |
|
(при необходимости применяют интерполяцию) |
|
Заключение в нетривиальном случае для биномиальной аппроксимации: |
|
Гипотезу Н0 отклоняют, если F2 ³ F1-a(f1, f2), в противном случае гипотезу Н0 не отклоняют. |
|
II Нормальная аппроксимация |
|
Вычисление статистики и определение значений по таблице 3 |
|
|
|
По таблице 3 для q = (1 - a) определяют u1-a = |
|
Заключение в нетривиальном случае для нормальной аппроксимации: |
|
Гипотезу Н0 отклоняют, если z2 ³ u1-, в противном случае гипотезу Н0 не отклоняют. |
|
Результат проверки гипотез: |
|
Гипотеза Н0 отклонена £ |
|
Гипотеза Н0 не отклонена £ |
8.3.2 Форма С-2. Сравнение двух пропорций для одностороннего критерия Н0: р1 £ р2
|
Характеристика: |
|
Процедура определения: |
|
Элементы: |
|
Критерий для идентификации целевых элементов: |
|
Примечания: |
|
Выбранный уровень значимости a = |
|
Объем выборки 1: п1 = |
|
Объем выборки 2: п2 = |
|
Число целевых элементов в выборке 1: х1 = |
|
Число целевых элементов в выборке 2: х2 = |
|
Проверка гипотез для тривиального случая |
|
|
|
Неравенство является истинным £ |
|
Неравенство не является истинным £ |
|
Если неравенство является истинным, гипотезу не отклоняют и результат проверки гипотезы может быть объявлен немедленно. В противном случае проводят следующую процедуру, которая может привести к отклонению или к неотклонению гипотезы Н0. |
|
Проверка гипотез для нетривиальных случаев |
|
Если, по крайней мере, одно из четырех значений п1, п2, (х1 + х2), (п1 + п2 - х1 - х2) меньше или равно (п1 + п2)/4, то применяют биномиальную аппроксимацию, приведенную в I настоящей формы; в противном случае применяют нормальную аппроксимацию, приведенную в II настоящей формы. Однако даже если вышеупомянутое условие выполнено, можно применять нормальную аппроксимацию, если выполнены два следующих условия: |
|
- при применении биномиальной аппроксимации в таблице 4 F-распределения необходимо использовать интерполяцию; |
|
- п1 и п2 или (х1 + х2) и (п1 + п2 - х1 - х2) попарно являются величинами одного порядка. |
|
Решение: |
|
Должна применяться биномиальная аппроксимация (продолжить I) £ |
|
Должна применяться нормальная аппроксимация (продолжить II) £ |
|
I Биномиальная аппроксимация |
|
Определение величин: К1, К2, h1, h2 |
|
Если [п2 < п1 и п2 < (х1 + х2)] или [(п1 + п2 - х1 - х2) < п1 и (п1 + п2 - х1 - х2) < (х1 + х2)], искомые величины определяют следующим образом: |
|
h1 = п2 = |
|
h2 = п1 = |
|
К1 = п2 - х2 = |
|
К2 = п1 - х1 = |
|
В противном случае: |
|
h1 = п1 = |
|
h2 = п2 = |
|
К1 = х1 = |
|
К2 = х2 = |
|
Вычисление статистики и определение значений по таблице 4 |
|
а) Случай h1 £ К1+ К2 £ |
|
|
|
Числа степеней свободы F-распределения: |
|
f1 = 2(h1 - К1 + 1) = |
|
f2 = 2К1 = |
|
По таблице 4 для q = (1 - a), f1 и f2 определяют F1 - a( f1, f2) = |
|
(при необходимости применяют интерполяцию) |
|
b) Случай h1 > К1+ К2 £ |
|
|
|
Число степеней свободы F-распределения: |
|
f1 = 2(К1 + 1) = |
|
f2 = 2К2 = |
|
По таблице 4 для q = (1 - a), f1 и f2 определяют F1 - a(f1, f2) = |
|
(при необходимости применяют интерполяцию) |
|
Заключение в нетривиальном случае для биномиальной аппроксимации: |
|
Гипотезу Н0 отклоняют, если F1 ³ F1-a(f1, f2), в противном случае гипотезу Н0 не отклоняют. |
|
II Нормальная аппроксимация |
|
Вычисление статистики и определение значений по таблице 3 |
|
|
|
По таблице 3 для q = (1 - a) определяют u1-a = |
|
Заключение в нетривиальном случае для нормальной аппроксимации: |
|
Гипотезу Н0 отклоняют, если z2 ³ u1-a, в противном случае гипотезу Н0 не отклоняют. |
|
Результат проверки гипотез: |
|
Гипотеза Н0 отклонена £ |
|
Гипотеза Н0 не отклонена £ |
8.3.3 Форма С-3. Сравнение двух пропорций для двустороннего критерия Н0: р1 = р2
|
Характеристика: |
|
Процедура определения: |
|
Элементы: |
|
Критерий для идентификации целевых элементов: |
|
Примечания: |
|
Выбранный уровень значимости a = |
|
Объем выборки 1: п1 = |
|
Объем выборки 2: п2 = |
|
Число целевых элементов в выборке 1: х1 = |
|
Число целевых элементов в выборке 2: х2 = |
|
Проверка гипотез для тривиального случая |
|
|
|
Неравенство является истинным £ |
|
Неравенство не является истинным £ |
|
Если неравенство является истинным, гипотезу не отклоняют и результат проверки гипотезы может быть объявлен немедленно. В противном случае проводят следующую процедуру, которая может привести к отклонению или к неотклонению гипотезы Н0. |
|
Проверка гипотез для нетривиальных случаев |
|
Если, по крайней мере, одно из четырех значений п1, п2, (х1 + х2), (п1 + п2 - х1 - х2) меньше или равно (п1 + п2)/4, то применяют биномиальную аппроксимацию, приведенную в I настоящей формы; в противном случае применяют нормальную аппроксимацию, приведенную в II настоящей формы. Однако даже если вышеупомянутое условие выполнено, можно применять нормальную аппроксимацию, если выполнены два следующих условия: |
|
- при применении биномиальной аппроксимации в таблице 4 F-распределения необходимо использовать интерполяцию; |
|
- п1 и п2 или (х1 + х2) и (п1 + п2 - х1 - х2) попарно являются величинами одного порядка. |
|
Решение: |
|
Должна применяться биномиальная аппроксимация (продолжить I) £ |
|
Должна применяться нормальная аппроксимация (продолжить II) £ |
|
I Биномиальная аппроксимация |
|
Определение величин: К1, К2, h1, h2 |
|
Если [п2 < п1 и п2 < (х1 + х2)] или [(п1 + п2 - х1 - х2) < п1 и (п1 + п2 - х1 - х2) < (х1 + х2)], искомые величины определяют следующим образом: |
|
h1 = п2 = |
|
h2 = п1 = |
|
К1 = п2 - х2 = |
|
К2 = п1 - х1 = |
|
В противном случае: |
|
h1 = п1 = |
|
h2 = п2 = |
|
К1 = х1 = |
|
К2 = х2 = |
|
Вычисление статистики и определение значений по таблице 4 |
|
а) Случай h1 £ К1 + К2 £ |
|
1) Случай |
|
Значения F1, f1 и f2 определяют по 8.3.2 (форма С-2) |
|
F1 = ; f1 = ; f2 = |
|
По таблице 4 для q = (1 - a/2), f1 и f2 (при необходимости применяют интерполяцию) определяют F1-a/2(f1, f2) = |
|
2) Случай |
|
Значения F2, f1 и f2 определяют по 8.3.1 (форма С-1) |
|
F2 = ; f1 = ; f2 = |
|
По таблице 4 для q = (1 - a/2), f1 и f2 (при необходимости применяют интерполяцию) определяют F1-a/2(f1, f2) = |
|
b) Случай h1 > К1 + К2 £ |
|
1) Случай |
|
Значения F1, f1 и f2 определяют по 8.3.2 (форма С-2) |
|
F1 = ; f1 = ; f2 = |
|
По таблице 4 для q = (1 - a/2), f1 и f2 (при необходимости применяют интерполяцию) определяют F1-a/2(f1, f2) = |
|
2) Случай |
|
Значения F2, f1 и f2 определяют по 8.3.1 (форма С-1). |
|
F2 = ; f1 = ; f2 = |
|
По таблице 4 для q = (1 - a/2), f1 и f2 (при необходимости применяют интерполяцию) определяют F1-a/2(f1, f2) = |
|
Заключение в нетривиальном случае для биномиальной аппроксимации |
|
Гипотезу Но отклоняют, если: |
|
F1 ³
F1-a/2(f1, f2) в случае |
|
или |
|
F2
³
F1-a/2(f1, f2) в
случае |
|
в противном случае гипотезу Н0 не отклоняют. |
|
II Нормальная аппроксимация Вычисление статистики и определение значений по таблице 3 |
|
а) Случай |
|
Значение z1 определяют по 8.3.2 (форма С-2) |
|
z1 = |
|
По таблице 3 для q = (1 - a/2) определяют u1-a/2 = |
|
b) Случай |
|
Значение z2 определяют по 8.3.1 (форма С-1) |
|
z2 = |
|
По таблице 3 для q = (1 - a/2) определяют u1-a/2 = |
|
Заключение в нетривиальном случае для нормальной аппроксимации Гипотезу Н0 отклоняют, если: |
|
z1 ³
u1-a/2 в случае |
|
или |
|
z2 ³ u1-a/2 в случае |
|
в противном случае гипотезу Н0 не отклоняют. |
|
Результат проверки гипотез: |
|
Гипотеза Н0 отклонена £ |
|
Гипотеза Н0 не отклонена £ |
9 Таблицы и номограммы
9.1 Интерполяция в таблице 4 квантилей F-распределения
Необходимо определить, что Fq(f1, f2) = F(f1, f2). Предположим, что в таблице 4 приведены смежные значения F(f11, f2) и F(f12, f2) с f11 < f1 < f12. Тогда

Интерполяцию по f2 выполняют аналогичным способом, если в таблице приведены смежные значения F(f1, f21) и F(f1, f22) с f21 < f2 < f22

Если искомое значение ни по f1 ни по f2 не приведено в таблице, необходимо выполнить три шага интерполяции.
Сначала выполняют два параллельных шага по одному из двух показателей числа степеней свободы, а затем - следующий шаг по другому показателю числа степеней свободы.
Если f1 > 30 и f2 > 30, квантиль F-распределения вычисляют по следующим уравнениям:
![]()
![]()
![]()
![]()
![]()
![]()
где ![]()
![]()
Fq(f1, f2) = Fq.
9.2 Пример
Пример для определения критического значения Сl,0 для нулевой гипотезы Н0: р ³ р0 отмечен в номограмме (рисунок 2) полужирной линией (см. 7.2.1). Заданы значения р0 = 0,15, a = 0,05 и п = 35. По номограмме определяют значение х между прямыми линиями 1 и 2. Таким образом, Сl,0 = 2.
Предположим, что объем выборки п не определен. Если помимо этого задано, что b = 0,10 и р' = 0,039, то вторую линию проводят от р' к 1–b для определения объема выборки. По точке пересечения этих двух линий в номограмме определяют, что п = 50 и х = 3. Таким образом, нулевую гипотезу Н0 принимают, если х £ 3, в противном случае принимают альтернативную гипотезу.
Таблица 2 - Верхние односторонние доверительные границы для пропорции р с п £ 30
|
n |
Значение х при q = 0,950 |
|||||||||||||||||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
|
1 |
0,950 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0,777 |
0,975 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0,632 |
0,865 |
0,984 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0,528 |
0,752 |
0,903 |
0,988 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0,451 |
0,658 |
0,811 |
0,924 |
0,990 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
0,394 |
0,582 |
0,729 |
0,847 |
0,938 |
0,992 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
0,349 |
0,521 |
0,659 |
0,775 |
0,872 |
0,947 |
0,993 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
0,313 |
0,471 |
0,600 |
0,711 |
0,808 |
0,889 |
0,954 |
0,994 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
0,284 |
0,430 |
0,550 |
0,656 |
0,749 |
0,832 |
0,903 |
0,959 |
0,995 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
0,259 |
0,395 |
0,507 |
0,607 |
0,697 |
0,778 |
0,850 |
0,913 |
0,964 |
0,995 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
0,239 |
0,365 |
0,471 |
0,565 |
0,651 |
0,729 |
0,801 |
0,865 |
0,922 |
0,967 |
0,996 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
0,221 |
0,339 |
0,439 |
0,528 |
0,610 |
0,685 |
0,755 |
0,819 |
0,878 |
0,929 |
0,970 |
0,996 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
0,206 |
0,317 |
0,411 |
0,495 |
0,573 |
0,646 |
0,713 |
0,777 |
0,835 |
0,888 |
0,934 |
0,972 |
0,997 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
0,193 |
0,297 |
0,386 |
0,466 |
0,541 |
0,610 |
0,675 |
0,737 |
0,794 |
0,848 |
0,896 |
0,939 |
0,975 |
0,997 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
0,182 |
0,280 |
0,364 |
0,440 |
0,511 |
0,578 |
0,641 |
0,701 |
0,757 |
0,810 |
0,859 |
0,904 |
0,944 |
0,976 |
0,997 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
0,171 |
0,264 |
0,344 |
0,417 |
0,485 |
0,549 |
0,609 |
0,667 |
0,722 |
0,774 |
0,823 |
0,868 |
0,910 |
0,947 |
0,978 |
0,997 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
0,162 |
0,251 |
0,327 |
0,396 |
0,461 |
0,522 |
0,581 |
0,636 |
0,690 |
0,740 |
0,789 |
0,834 |
0,877 |
0,916 |
0,951 |
0,979 |
0,997 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
0,154 |
0,238 |
0,311 |
0,377 |
0,439 |
0,498 |
0,555 |
0,608 |
0,660 |
0,709 |
0,757 |
0,802 |
0,844 |
0,884 |
0,921 |
0,953 |
0,980 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
0,146 |
0,227 |
0,296 |
0,360 |
0,420 |
0,476 |
0,530 |
0,582 |
0,632 |
0,680 |
0,727 |
0,771 |
0,813 |
0,853 |
0,891 |
0,925 |
0,956 |
0,981 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
0,140 |
0,217 |
0,283 |
0,344 |
0,402 |
0,456 |
0,508 |
0,559 |
0,607 |
0,654 |
0,699 |
0,742 |
0,783 |
0,823 |
0,861 |
0,896 |
0,929 |
0,958 |
0,982 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
21 |
0,133 |
0,207 |
0,271 |
0,330 |
0,385 |
0,437 |
0,488 |
0,536 |
0,583 |
0,629 |
0,672 |
0,715 |
0,756 |
0,795 |
0,832 |
0,868 |
0,902 |
0,933 |
0,960 |
0,983 |
0,998 |
|
|
|
|
|
|
|
|
|
|
22 |
0,128 |
0,199 |
0,260 |
0,316 |
0,370 |
0,420 |
0,469 |
0,516 |
0,561 |
0,605 |
0,648 |
0,689 |
0,729 |
0,768 |
0,805 |
0,841 |
0,874 |
0,906 |
0,936 |
0,962 |
0,984 |
0,998 |
|
|
|
|
|
|
|
|
|
23 |
0,123 |
0,191 |
0,250 |
0,304 |
0,355 |
0,404 |
0,451 |
0,497 |
0,541 |
0,584 |
0,625 |
0,665 |
0,704 |
0,742 |
0,779 |
0,814 |
0,848 |
0,880 |
0,911 |
0,939 |
0,964 |
0,985 |
0,998 |
|
|
|
|
|
|
|
|
24 |
0,118 |
0,183 |
0,240 |
0,293 |
0,342 |
0,390 |
0,435 |
0,479 |
0,522 |
0,563 |
0,604 |
0,643 |
0,681 |
0,718 |
0,754 |
0,789 |
0,823 |
0,855 |
0,886 |
0,915 |
0,941 |
0,966 |
0,985 |
0,998 |
|
|
|
|
|
|
|
25 |
0,113 |
0,177 |
0,232 |
0,282 |
0,330 |
0,376 |
0,420 |
0,463 |
0,504 |
0,544 |
0,584 |
0,622 |
0,659 |
0,695 |
0,731 |
0,765 |
0,798 |
0,830 |
0,861 |
0,890 |
0,918 |
0,944 |
0,967 |
0,986 |
0,998 |
|
|
|
|
|
|
26 |
0,109 |
0,170 |
0,223 |
0,272 |
0,319 |
0,363 |
0,406 |
0,447 |
0,487 |
0,527 |
0,565 |
0,602 |
0,638 |
0,674 |
0,708 |
0,742 |
0,775 |
0,807 |
0,837 |
0,867 |
0,895 |
0,922 |
0,946 |
0,968 |
0,987 |
0,999 |
|
|
|
|
|
27 |
0,106 |
0,164 |
0,216 |
0,263 |
0,308 |
0,351 |
0,393 |
0,433 |
0,472 |
0,510 |
0,547 |
0,583 |
0,619 |
0,654 |
0,687 |
0,720 |
0,753 |
0,784 |
0,814 |
0,844 |
0,872 |
0,899 |
0,925 |
0,948 |
0,970 |
0,987 |
0,999 |
|
|
|
|
28 |
0,102 |
0,159 |
0,209 |
0,255 |
0,298 |
0,340 |
0,380 |
0,419 |
0,457 |
0,494 |
0,530 |
0,566 |
0,600 |
0,634 |
0,667 |
0,700 |
0,731 |
0,762 |
0,792 |
0,821 |
0,850 |
0,877 |
0,903 |
0,927 |
0,950 |
0,971 |
0,988 |
0,999 |
|
|
|
29 |
0,099 |
0,154 |
0,202 |
0,247 |
0,289 |
0,329 |
0,368 |
0,406 |
0,443 |
0,480 |
0,515 |
0,549 |
0,583 |
0,616 |
0,648 |
0,680 |
0,711 |
0,742 |
0,771 |
0,800 |
0,828 |
0,855 |
0,881 |
0,906 |
0,930 |
0,952 |
0,972 |
0,988 |
0,999 |
|
|
30 |
0,096 |
0,149 |
0,196 |
0,239 |
0,280 |
0,319 |
0,358 |
0,394 |
0,430 |
0,466 |
0,500 |
0,534 |
0,567 |
0,599 |
0,631 |
0,662 |
0,692 |
0,722 |
0,751 |
0,779 |
0,807 |
0,834 |
0,860 |
0,886 |
0,910 |
0,932 |
0,954 |
0,973 |
0,989 |
0,999 |
Продолжение таблицы 2
|
п |
Значение х при q = 0,975 |
|||||||||||||||||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
|
1 |
0,975 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0,842 |
0,988 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0,708 |
0,906 |
0,992 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0,603 |
0,806 |
0,933 |
0,994 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0,522 |
0,717 |
0,854 |
0,948 |
0,995 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
0,460 |
0,642 |
0,778 |
0,882 |
0,957 |
0,996 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
0,410 |
0,579 |
0,710 |
0,816 |
0,902 |
0,964 |
0,997 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
0,370 |
0,527 |
0,651 |
0,756 |
0,843 |
0,915 |
0,969 |
0,997 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
0.337 |
0,483 |
0,601 |
0,701 |
0,788 |
0,864 |
0,926 |
0,972 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
0,309 |
0,446 |
0,557 |
0,653 |
0,738 |
0,813 |
0,879 |
0,934 |
0,975 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
0,285 |
0,413 |
0,518 |
0,610 |
0,693 |
0,767 |
0,833 |
0,891 |
0,940 |
0,978 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
0,265 |
0,385 |
0,485 |
0,572 |
0,652 |
0,724 |
0,790 |
0,849 |
0,901 |
0,946 |
0,980 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
0,248 |
0,361 |
0,455 |
0,539 |
0,615 |
0,685 |
0,749 |
0,808 |
0,862 |
0,910 |
0,950 |
0,981 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
0,232 |
0,339 |
0,429 |
0,508 |
0,582 |
0,649 |
0,712 |
0,770 |
0,824 |
0,873 |
0,917 |
0,954 |
0,983 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
0,219 |
0,320 |
0,405 |
0,481 |
0,552 |
0,617 |
0,678 |
0,735 |
0,788 |
0,837 |
0,882 |
0,923 |
0,957 |
0,984 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
0,206 |
0,384 |
0,457 |
0,524 |
0,587 |
0,646 |
0,702 |
0,754 |
0,803 |
0,849 |
0,890 |
0,928 |
0,960 |
0,985 |
0,999 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
0,196 |
0,365 |
0,435 |
0,499 |
0,560 |
0,617 |
0,671 |
0,722 |
0,771 |
0,816 |
0,858 |
0,897 |
0,932 |
0,963 |
0,986 |
0,987 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
0,186 |
0,348 |
0,415 |
0,477 |
0,535 |
0,591 |
0,643 |
0,693 |
0,740 |
0,785 |
0,828 |
0,867 |
0,904 |
0,936 |
0,965 |
0,967 |
0,987 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
0,177 |
0,332 |
0,396 |
0,456 |
0,513 |
0,566 |
0,617 |
0,666 |
0,712 |
0,756 |
0,798 |
0,838 |
0,875 |
0,909 |
0,940 |
0,943 |
0,968 |
0,988 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
0,169 |
0,317 |
0,379 |
0,437 |
0,492 |
0,543 |
0,593 |
0,640 |
0,685 |
0,729 |
0,770 |
0,809 |
0,847 |
0,882 |
0,914 |
0,918 |
0,946 |
0,970 |
0,989 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
21 |
0,162 |
0,304 |
0,364 |
0,420 |
0,472 |
0,522 |
0,570 |
0,616 |
0,660 |
0,703 |
0,743 |
0,782 |
0,819 |
0,855 |
0,888 |
0,893 |
0,922 |
0,949 |
0,971 |
0,989 |
0,999 |
|
|
|
|
|
|
|
|
|
|
22 |
0,155 |
0,292 |
0,350 |
0,403 |
0,454 |
0,503 |
0,549 |
0,594 |
0,637 |
0,678 |
0,718 |
0,757 |
0,793 |
0,829 |
0,862 |
0,868 |
0,898 |
0,926 |
0,951 |
0,973 |
0,990 |
0,999 |
|
|
|
|
|
|
|
|
|
23 |
0,149 |
0,281 |
0,336 |
0,388 |
0,438 |
0,485 |
0,530 |
0,573 |
0,615 |
0,656 |
0,695 |
0,732 |
0,769 |
0,803 |
0,837 |
0,844 |
0,874 |
0,903 |
0,929 |
0,953 |
0,974 |
0,990 |
0,999 |
|
|
|
|
|
|
|
|
24 |
0,143 |
0,270 |
0,324 |
0,374 |
0,422 |
0,468 |
0,511 |
0,554 |
0,595 |
0,634 |
0,672 |
0,709 |
0,745 |
0,779 |
0,813 |
0,821 |
0,851 |
0,880 |
0,907 |
0,932 |
0,955 |
0,975 |
0,991 |
1 |
|
|
|
|
|
|
|
25 |
0,138 |
0,261 |
0,313 |
0,361 |
0,408 |
0,452 |
0,494 |
0,536 |
0,575 |
0,614 |
0,651 |
0,687 |
0,723 |
0,756 |
0,789 |
0,798 |
0,828 |
0,857 |
0,885 |
0,911 |
0,935 |
0,957 |
0,976 |
0,999 |
1 |
|
|
|
|
|
|
26 |
0,133 |
0,252 |
0,302 |
0,349 |
0,394 |
0,437 |
0,478 |
0,518 |
0,557 |
0,595 |
0,631 |
0,667 |
0,701 |
0,735 |
0,767 |
0,777 |
0,806 |
0,835 |
0,863 |
0,889 |
0,914 |
0,937 |
0,959 |
0,991 |
0,999 |
1 |
|
|
|
|
|
27 |
0,128 |
0,243 |
0,292 |
0,338 |
0,381 |
0,423 |
0,463 |
0,502 |
0,540 |
0,577 |
0,613 |
0,647 |
0,681 |
0,714 |
0,746 |
0,756 |
0,785 |
0,814 |
0,842 |
0,868 |
0,894 |
0,918 |
0,940 |
0,977 |
0,991 |
0,991 |
1 |
|
|
|
|
28 |
0,124 |
0,236 |
0,283 |
0,327 |
0,369 |
0,410 |
0,449 |
0,487 |
0,524 |
0,560 |
0,595 |
0,629 |
0,662 |
0,694 |
0,725 |
0,736 |
0,765 |
0,794 |
0,821 |
0,848 |
0,873 |
0,898 |
0,921 |
0,960 |
0,978 |
0,978 |
0,992 |
1 |
|
|
|
29 |
0,120 |
0,228 |
0,274 |
0,317 |
0,358 |
0,398 |
0,436 |
0,473 |
0,509 |
0,544 |
0,578 |
0,611 |
0,644 |
0,675 |
0,706 |
0,717 |
0,746 |
0,774 |
0,801 |
0,828 |
0,853 |
0,878 |
0,901 |
0,942 |
0,962 |
0,962 |
0,979 |
0,992 |
1 |
|
|
30 |
0,116 |
0,221 |
0,266 |
0,308 |
0,348 |
0,386 |
0,423 |
0,459 |
0,494 |
0,529 |
0,562 |
0,594 |
0,626 |
0,657 |
0,688 |
0,999 |
0,999 |
0,999 |
0,999 |
0,999 |
0,999 |
0,999 |
0,999 |
0,923 |
0,944 |
0,944 |
0,963 |
0,979 |
0,992 |
1 |
Продолжение таблицы 2
|
п |
Значение хпри q = 0,990 |
|||||||||||||||||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
|
1 |
0,990 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0,900 |
0,995 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0,785 |
0,942 |
0,997 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0,684 |
0,860 |
0,959 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0,602 |
0,778 |
0,895 |
0,968 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
0,536 |
0,706 |
0,827 |
0,916 |
0,974 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
0,483 |
0,644 |
0,764 |
0,858 |
0,930 |
0,978 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
0,438 |
0,590 |
0,707 |
0,802 |
0,880 |
0,940 |
0,981 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
0,401 |
0,545 |
0,657 |
0,750 |
0,830 |
0,895 |
0,947 |
0,983 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
0,370 |
0,505 |
0,612 |
0,703 |
0,782 |
0,850 |
0,907 |
0,953 |
0,985 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
0,343 |
0,470 |
0,573 |
0,661 |
0,738 |
0,807 |
0,866 |
0,917 |
0,958 |
0,986 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
0,319 |
0,440 |
0,538 |
0,623 |
0,698 |
0,766 |
0,826 |
0,879 |
0,925 |
0,962 |
0,988 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
0,299 |
0,413 |
0,507 |
0,588 |
0,661 |
0,728 |
0,788 |
0,842 |
0,890 |
0,931 |
0,965 |
0,989 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
0,281 |
0,390 |
0,479 |
0,557 |
0,628 |
0,693 |
0,752 |
0,806 |
0,855 |
0,899 |
0,936 |
0,967 |
0,990 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
0,265 |
0,368 |
0,454 |
0,529 |
0,597 |
0,660 |
0,718 |
0,772 |
0,821 |
0,866 |
0,906 |
0,941 |
0,970 |
0,990 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
0,251 |
0,349 |
0,431 |
0,503 |
0,569 |
0,630 |
0,687 |
0,740 |
0,789 |
0,834 |
0,875 |
0,913 |
0,945 |
0,972 |
0,991 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
0,238 |
0,332 |
0,410 |
0,480 |
0,544 |
0,603 |
0,658 |
0,710 |
0,758 |
0,803 |
0,845 |
0,884 |
0,918 |
0,949 |
0,974 |
0,992 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
0,226 |
0,317 |
0,392 |
0,459 |
0,520 |
0,578 |
0,631 |
0,682 |
0,729 |
0,774 |
0,816 |
0,855 |
0,891 |
0,923 |
0,952 |
0,975 |
0,992 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
0,216 |
0,302 |
0,375 |
0,439 |
0,499 |
0,554 |
0,607 |
0,656 |
0,702 |
0,747 |
0,788 |
0,827 |
0,864 |
0,897 |
0,928 |
0,954 |
0,977 |
0,992 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
0,206 |
0,289 |
0,359 |
0,421 |
0,479 |
0,533 |
0,583 |
0,631 |
0,677 |
0,720 |
0,762 |
0,800 |
0,837 |
0,871 |
0,903 |
0,932 |
0,957 |
0,978 |
0,993 |
1 |
|
|
|
|
|
|
|
|
|
|
|
21 |
0,197 |
0,277 |
0,344 |
0,405 |
0,460 |
0,512 |
0,562 |
0,609 |
0,653 |
0,696 |
0,736 |
0,775 |
0,811 |
0,846 |
0,878 |
0,908 |
0,935 |
0,959 |
0,979 |
0,993 |
1 |
|
|
|
|
|
|
|
|
|
|
22 |
0,189 |
0,266 |
0,331 |
0,389 |
0,443 |
0,494 |
0,542 |
0,587 |
0,631 |
0,673 |
0,712 |
0,750 |
0,787 |
0,821 |
0,854 |
0,884 |
0,913 |
0,938 |
0,961 |
0,980 |
0,994 |
1 |
|
|
|
|
|
|
|
|
|
23 |
0,182 |
0,256 |
0,319 |
0,375 |
0,427 |
0,476 |
0,523 |
0,567 |
0,610 |
0,651 |
0,690 |
0,727 |
0,763 |
0,797 |
0,830 |
0,861 |
0,890 |
0,917 |
0,941 |
0,963 |
0,981 |
0,994 |
1 |
|
|
|
|
|
|
|
|
24 |
0,175 |
0,247 |
0,307 |
0,362 |
0,412 |
0,460 |
0,505 |
0,549 |
0,590 |
0,630 |
0,668 |
0,705 |
0,741 |
0,775 |
0,807 |
0,838 |
0,867 |
0,895 |
0,921 |
0,944 |
0,965 |
0,982 |
0,994 |
1 |
|
|
|
|
|
|
|
25 |
0,169 |
0,238 |
0,296 |
0,349 |
0,398 |
0,445 |
0,489 |
0,531 |
0,572 |
0,611 |
0,648 |
0,684 |
0,719 |
0,753 |
0,785 |
0,816 |
0,845 |
0,873 |
0,899 |
0,924 |
0,946 |
0,966 |
0,982 |
0,994 |
1 |
|
|
|
|
|
|
26 |
0,163 |
0,230 |
0,286 |
0,338 |
0,385 |
0,430 |
0,473 |
0,515 |
0,554 |
0,592 |
0,629 |
0,664 |
0,699 |
0,732 |
0,764 |
0,794 |
0,824 |
0,852 |
0,879 |
0,904 |
0,927 |
0,948 |
0,967 |
0,983 |
0,995 |
1 |
|
|
|
|
|
27 |
0,157 |
0,222 |
0,277 |
0,327 |
0,373 |
0,417 |
0,459 |
0,499 |
0,538 |
0,575 |
0,611 |
0,646 |
0,679 |
0,712 |
0,743 |
0,774 |
0,803 |
0,831 |
0,858 |
0,883 |
0,908 |
0,930 |
0,951 |
0,969 |
0,984 |
0,995 |
1 |
|
|
|
|
28 |
0,152 |
0,215 |
0,268 |
0,317 |
0,362 |
0,404 |
0,445 |
0,484 |
0,522 |
0,558 |
0,594 |
0,628 |
0,661 |
0,693 |
0,724 |
0,754 |
0,783 |
0,811 |
0,838 |
0,864 |
0,888 |
0,911 |
0,933 |
0,952 |
0,970 |
0,984 |
0,995 |
1 |
|
|
|
29 |
0,147 |
0,208 |
0,260 |
0,307 |
0,351 |
0,393 |
0,432 |
0,470 |
0,507 |
0,543 |
0,577 |
0,611 |
0,643 |
0,675 |
0,705 |
0,735 |
0,764 |
0,791 |
0,818 |
0,844 |
0,869 |
0,892 |
0,914 |
0,935 |
0,954 |
0,971 |
0,985 |
0,995 |
1 |
|
|
30 |
0,143 |
0,202 |
0,252 |
0,298 |
0,341 |
0,381 |
0,420 |
0,457 |
0,493 |
0,528 |
0,562 |
0,594 |
0,626 |
0,657 |
0,687 |
0,717 |
0,745 |
0,773 |
0,799 |
0,825 |
0,850 |
0,874 |
0,896 |
0,918 |
0,937 |
0,956 |
0,972 |
0,986 |
0,995 |
1 |
Окончание таблицы 2
|
п |
Значение х при q = 0,995 |
|||||||||||||||||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
|
1 |
0,995 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0,930 |
0,998 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0,830 |
0,959 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0,735 |
0,890 |
0,971 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0,654 |
0,815 |
0,918 |
0,978 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
0,587 |
0,747 |
0,857 |
0,934 |
0,982 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
0,531 |
0,685 |
0,798 |
0,883 |
0,945 |
0,985 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
0,485 |
0,632 |
0,743 |
0,831 |
0,901 |
0,953 |
0,987 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
0,445 |
0,585 |
0,693 |
0,781 |
0,854 |
0,914 |
0,959 |
0,988 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
0,412 |
0,545 |
0,649 |
0,736 |
0,810 |
0,872 |
0,924 |
0,963 |
0,990 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
0,383 |
0,509 |
0,609 |
0,694 |
0,767 |
0,831 |
0,886 |
0,932 |
0,967 |
0,991 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
0,357 |
0,478 |
0,573 |
0,656 |
0,728 |
0,792 |
0,848 |
0,897 |
0,938 |
0,970 |
0,992 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
0,335 |
0,450 |
0,542 |
0,621 |
0,692 |
0,755 |
0,812 |
0,862 |
0,906 |
0,943 |
0,973 |
0,992 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
0,316 |
0,425 |
0,513 |
0,590 |
0,658 |
0,721 |
0,777 |
0,828 |
0,874 |
0,914 |
0,948 |
0,975 |
0,993 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
0,298 |
0,402 |
0,487 |
0,561 |
0,628 |
0,689 |
0,744 |
0,795 |
0,842 |
0,884 |
0,920 |
0,952 |
0,977 |
0,993 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
0,282 |
0,382 |
0,463 |
0,535 |
0,600 |
0,659 |
0,714 |
0,764 |
0,811 |
0,853 |
0,892 |
0,926 |
0,955 |
0,978 |
0,994 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
0,268 |
0,364 |
0,442 |
0,511 |
0,574 |
0,631 |
0,685 |
0,735 |
0,781 |
0,824 |
0,863 |
0,899 |
0,931 |
0,958 |
0,980 |
0,994 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
0,255 |
0,347 |
0,422 |
0,489 |
0,550 |
0,606 |
0,658 |
0,707 |
0,753 |
0,796 |
0,836 |
0,872 |
0,905 |
0,935 |
0,960 |
0,981 |
0,995 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
0,244 |
0,332 |
0,404 |
0,469 |
0,528 |
0,582 |
0,633 |
0,681 |
0,727 |
0,769 |
0,809 |
0,846 |
0,880 |
0,911 |
0,939 |
0,963 |
0,982 |
0,995 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
0,233 |
0,318 |
0,388 |
0,450 |
0,507 |
0,560 |
0,610 |
0,657 |
0,701 |
0,743 |
0,783 |
0,820 |
0,855 |
0,887 |
0,916 |
0,942 |
0,965 |
0,983 |
0,995 |
1 |
|
|
|
|
|
|
|
|
|
|
|
21 |
0,223 |
0,305 |
0,372 |
0,433 |
0,488 |
0,540 |
0,588 |
0,634 |
0,678 |
0,719 |
0,758 |
0,795 |
0,830 |
0,862 |
0,893 |
0,920 |
0,945 |
0,967 |
0,984 |
0,995 |
1 |
|
|
|
|
|
|
|
|
|
|
22 |
0,215 |
0,293 |
0,358 |
0,417 |
0,470 |
0,521 |
0,568 |
0,613 |
0,655 |
0,696 |
0,735 |
0,771 |
0,806 |
0,839 |
0,870 |
0,898 |
0,924 |
0,948 |
0,968 |
0,985 |
0,996 |
1 |
|
|
|
|
|
|
|
|
|
23 |
0,206 |
0,282 |
0,345 |
0,402 |
0,454 |
0,503 |
0,549 |
0,593 |
0,634 |
0,674 |
0,712 |
0,748 |
0,783 |
0,816 |
0,847 |
0,876 |
0,903 |
0,928 |
0,950 |
0,970 |
0,985 |
0,996 |
1 |
|
|
|
|
|
|
|
|
24 |
0,199 |
0,272 |
0,333 |
0,388 |
0,438 |
0,486 |
0,531 |
0,574 |
0,614 |
0,654 |
0,691 |
0,727 |
0,761 |
0,794 |
0,825 |
0,854 |
0,882 |
0,908 |
0,931 |
0,953 |
0,971 |
0,986 |
0,996 |
1 |
|
|
|
|
|
|
|
25 |
0,191 |
0,262 |
0,322 |
0,375 |
0,424 |
0,470 |
0,514 |
0,556 |
0,596 |
0,634 |
0,671 |
0,706 |
0,740 |
0,772 |
0,803 |
0,833 |
0,861 |
0,887 |
0,912 |
0,934 |
0,955 |
0,972 |
0,987 |
0,996 |
1 |
|
|
|
|
|
|
26 |
0,185 |
0,253 |
0,311 |
0,363 |
0,410 |
0,456 |
0,498 |
0,539 |
0,578 |
0,615 |
0,652 |
0,686 |
0,720 |
0,752 |
0,782 |
0,812 |
0,840 |
0,867 |
0,892 |
0,915 |
0,937 |
0,956 |
0,973 |
0,987 |
0,996 |
1 |
|
|
|
|
|
27 |
0,179 |
0,245 |
0,301 |
0,351 |
0,398 |
0,442 |
0,483 |
0,523 |
0,561 |
0,598 |
0,633 |
0,667 |
0,700 |
0,732 |
0,762 |
0,792 |
0,820 |
0,847 |
0,872 |
0,896 |
0,919 |
0,940 |
0,958 |
0,974 |
0,988 |
0,997 |
1 |
|
|
|
|
28 |
0,173 |
0.237 |
0,292 |
0,340 |
0,386 |
0,429 |
0,469 |
0,508 |
0,545 |
0,581 |
0,616 |
0,650 |
0,682 |
0,713 |
0,743 |
0,772 |
0,800 |
0,827 |
0,853 |
0,877 |
0,900 |
0,922 |
0,942 |
0,960 |
0,975 |
0,988 |
0,997 |
1 |
|
|
|
29 |
0,167 |
0,230 |
0,283 |
0,330 |
0,375 |
0,416 |
0,456 |
0,494 |
0,530 |
0,566 |
0,600 |
0,632 |
0,664 |
0,695 |
0,725 |
0,754 |
0,781 |
0,808 |
0,834 |
0,859 |
0,882 |
0,904 |
0,925 |
0,944 |
0,961 |
0,976 |
0,989 |
0,997 |
1 |
|
|
30 |
0,162 |
0,223 |
0,275 |
0,321 |
0,364 |
0,405 |
0,443 |
0,480 |
0,516 |
0,551 |
0,584 |
0,616 |
0,647 |
0,678 |
0,707 |
0,736 |
0,763 |
0,790 |
0,815 |
0,840 |
0,864 |
0,886 |
0,908 |
0,928 |
0,946 |
0,963 |
0,977 |
0,989 |
0,997 |
1 |
Таблица 3 - Квантили стандартного нормального распределения uq
|
q = Ф(u) |
uq |
|
0,950 |
1,645 |
|
0,975 |
1,960 |
|
0,990 |
2,326 |
|
0,995 |
2,576 |

Рисунок 1 - Квантили F-распределения
Таблица 4 - Квантили F-распределения (см. рисунок 1)
|
f2 |
q |
f1 |
|||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
30 |
50 |
¥ |
||
|
1 |
0,9 |
39,9 |
49,5 |
53,6 |
55,8 |
57,2 |
58,2 |
58,9 |
59,4 |
59,9 |
60,2 |
60,7 |
61,2 |
61,7 |
62,3 |
62,7 |
63,3 |
|
|
0,95 |
161 |
200 |
216 |
225 |
230 |
234 |
237 |
239 |
241 |
242 |
244 |
246 |
248 |
250 |
252 |
254 |
|
|
0,975 |
648 |
800 |
864 |
900 |
922 |
937 |
948 |
957 |
963 |
969 |
977 |
985 |
993 |
1001 |
1008 |
1018 |
|
|
0,990 |
4052 |
5000 |
5403 |
5625 |
5764 |
5859 |
5928 |
5981 |
6022 |
6056 |
6106 |
6157 |
6209 |
6261 |
6303 |
6366 |
|
|
0,995 |
16210 |
20000 |
21610 |
22500 |
23060 |
23440 |
23710 |
23930 |
24090 |
24220 |
24430 |
24630 |
24840 |
25040 |
25210 |
25460 |
|
|
0,999 |
405300 |
500000 |
540400 |
562500 |
576400 |
585900 |
592900 |
598100 |
602300 |
605600 |
610700 |
615800 |
620900 |
626100 |
630300 |
636600 |
|
2 |
0,9 |
8,53 |
9,0 |
9,16 |
9,24 |
9,29 |
9,33 |
9,35 |
9,37 |
9,38 |
9,39 |
9,41 |
9,42 |
9,44 |
9,46 |
9,47 |
9,49 |
|
|
0,95 |
18,5 |
19,0 |
19,2 |
19,2 |
19,3 |
19,3 |
19,4 |
19,4 |
19,4 |
19,4 |
19,4 |
19,4 |
19,4 |
19,5 |
19,5 |
19,5 |
|
|
0,975 |
38,5 |
39,0 |
39,2 |
39,2 |
39,3 |
39,3 |
39,4 |
39,4 |
39,4 |
39,4 |
39,4 |
39,4 |
39,4 |
39,5 |
39,5 |
39,5 |
|
|
0,990 |
98,5 |
99,0 |
99,2 |
99,2 |
99,3 |
99,3 |
99,4 |
99,4 |
99,4 |
99,4 |
99,4 |
99,4 |
99,4 |
99,5 |
99,5 |
99 |
|
|
0,995 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
199 |
|
|
0,999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
999 |
|
3 |
0,9 |
5,54 |
5,46 |
5,39 |
5,34 |
5,31 |
5,28 |
5,27 |
5,25 |
5,24 |
5,23 |
5,22 |
5,20 |
5,18 |
5,17 |
5,15 |
5,13 |
|
|
0,95 |
10,1 |
9,55 |
9,28 |
9,12 |
9,01 |
8,94 |
8,89 |
8,85 |
8,81 |
8,79 |
8,74 |
8,70 |
8,66 |
8,62 |
8,58 |
8,53 |
|
|
0,975 |
17,4 |
16,0 |
15,4 |
15,1 |
14,9 |
14,7 |
14,6 |
14,5 |
14,5 |
14,4 |
14,3 |
14,3 |
14,2 |
14,1 |
14,0 |
13,9 |
|
|
0,990 |
34,1 |
30,8 |
29,5 |
28,7 |
28,2 |
27,9 |
27,7 |
27,5 |
27,3 |
27,2 |
27,1 |
26,9 |
26,7 |
26,5 |
26,4 |
26,1 |
|
|
0,995 |
55,6 |
49,8 |
47,5 |
46,2 |
45,4 |
44,8 |
44,4 |
44,1 |
43,9 |
43,7 |
43,4 |
43,1 |
42,8 |
42,5 |
42,2 |
41,8 |
|
|
0,999 |
167 |
149 |
141 |
137 |
135 |
133 |
132 |
131 |
130 |
129 |
128 |
127 |
126 |
125 |
125 |
123 |
|
4 |
0,9 |
4,54 |
4,32 |
4,19 |
4,11 |
4,05 |
4,01 |
3,98 |
3,95 |
3,94 |
3,92 |
3,90 |
3,87 |
3,84 |
3,82 |
3,80 |
3,76 |
|
|
0,95 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,09 |
6,04 |
6,00 |
5,96 |
5,91 |
5,86 |
5,80 |
5,75 |
5,70 |
5,63 |
|
|
0,975 |
12,2 |
10,6 |
9,98 |
9,60 |
9,36 |
9,20 |
3,07 |
8,96 |
8,90 |
8,84 |
8,75 |
8,66 |
8,56 |
8,46 |
8,38 |
8,26 |
|
|
0,990 |
21,2 |
18,0 |
16,7 |
16,04 |
15,5 |
15,2 |
15,0 |
14,8 |
14,7 |
14,5 |
14,4 |
14,2 |
14,0 |
13,8 |
13,7 |
13,5 |
|
|
0,995 |
31,3 |
26,3 |
24,3 |
23,2 |
22,5 |
22,0 |
21,6 |
21,4 |
21,1 |
21,0 |
20,7 |
20,4 |
20,2 |
19,9 |
19,7 |
19,3 |
|
|
0,999 |
74,1 |
61,2 |
56,2 |
53,4 |
51,7 |
50,5 |
49,7 |
49,0 |
48,5 |
48,1 |
47,4 |
46,8 |
46,1 |
45,4 |
44,9 |
44,1 |
|
5 |
0,9 |
4,06 |
3,78 |
3,62 |
3,52 |
3,45 |
3,40 |
3,37 |
3,34 |
3,32 |
3,30 |
3,27 |
3,24 |
3,21 |
3,17 |
3,15 |
3,10 |
|
|
0,95 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4,95 |
4,88 |
4,82 |
4,77 |
4,74 |
4,68 |
4,62 |
4,56 |
4,50 |
4,44 |
4,36 |
|
|
0,975 |
10,0 |
8,43 |
7,76 |
7,39 |
7,15 |
6,98 |
6,85 |
6,76 |
6,68 |
6,62 |
6,52 |
6,43 |
6,33 |
6,23 |
6,14 |
6,02 |
|
|
0,990 |
16,3 |
13,3 |
12,1 |
11,4 |
11,0 |
10,7 |
10,5 |
10,3 |
10,2 |
10,1 |
9,89 |
9,72 |
9,55 |
9,38 |
9,24 |
9,02 |
|
|
0,995 |
22,8 |
18,3 |
16,5 |
15,6 |
14,9 |
14,5 |
14,2 |
14,0 |
13,8 |
13,6 |
13,4 |
13,1 |
12,9 |
12,7 |
12,5 |
12,1 |
|
|
0,999 |
47,2 |
37,1 |
33,2 |
31,1 |
29,8 |
28,8 |
28,2 |
27,6 |
27,2 |
26,9 |
26,4 |
25,9 |
25,4 |
24,9 |
24,4 |
23,8 |
|
6 |
0,9 |
3,78 |
3,46 |
3,29 |
3,18 |
3,11 |
3,05 |
3,01 |
2,98 |
2,96 |
2,94 |
2,90 |
2,87 |
2,84 |
2,80 |
2,77 |
2,72 |
|
|
0,95 |
5,99 |
5,14 |
4,76 |
4,53 |
4,39 |
4,28 |
4,21 |
4,15 |
4,10 |
4,06 |
4,00 |
3,94 |
3,87 |
3,81 |
3,75 |
3,67 |
|
|
0,975 |
8,81 |
7,26 |
6,60 |
6,23 |
5,99 |
5,82 |
5,70 |
5,60 |
5,52 |
5,46 |
5,37 |
5,27 |
5,17 |
5,07 |
4,98 |
4,85 |
|
|
0,990 |
13,7 |
10,9 |
9,78 |
9,15 |
8,75 |
8,47 |
8,26 |
8,10 |
7,98 |
7,87 |
7,72 |
7,56 |
7,40 |
7,23 |
7,09 |
6,88 |
|
|
0,995 |
18,6 |
14,5 |
12,9 |
12,0 |
11,5 |
11,1 |
10,8 |
10,6 |
10,4 |
10,3 |
10,0 |
9,81 |
9,59 |
9,36 |
9,17 |
8,88 |
|
|
0,999 |
35,5 |
27,0 |
23,7 |
21,9 |
20,8 |
20,0 |
19,5 |
19,0 |
18,7 |
18,4 |
18,0 |
17,6 |
17,1 |
16,7 |
16,3 |
15,7 |
|
7 |
0,9 |
3,59 |
3,26 |
3,07 |
2,96 |
2,88 |
2,83 |
2,78 |
2,75 |
2,72 |
2,70 |
2,67 |
2,63 |
2,59 |
2,56 |
2,52 |
2,47 |
|
|
0,95 |
5,59 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,79 |
3,73 |
3,68 |
3,64 |
3,57 |
3,51 |
3,44 |
3,38 |
3,32 |
3,23 |
|
|
0,975 |
8,07 |
6,54 |
5,89 |
5,52 |
5,29 |
5,12 |
4,99 |
4,90 |
4,82 |
4,76 |
4,67 |
4,57 |
4,47 |
4,36 |
4,28 |
4,14 |
|
|
0,990 |
12,2 |
9,55 |
8,45 |
7,85 |
7,46 |
7,19 |
6,99 |
6,84 |
6,72 |
6,62 |
6,47 |
6,31 |
6,16 |
5,99 |
5,86 |
5,65 |
|
|
0,995 |
16,2 |
12,4 |
10,9 |
10,1 |
9,52 |
9,16 |
8,89 |
8,68 |
8,51 |
8,38 |
8,18 |
7,97 |
7,75 |
7,53 |
7,35 |
7,08 |
|
|
0,999 |
29,2 |
21,7 |
18,8 |
17,2 |
16,2 |
15,5 |
15,0 |
14,6 |
14,3 |
14,1 |
13,7 |
13,3 |
12,9 |
12,5 |
12,2 |
11,7 |
|
8 |
0,9 |
3,46 |
3,11 |
2,92 |
2,81 |
2,73 |
2,67 |
2,62 |
2,59 |
2,56 |
2,54 |
2,50 |
2,46 |
2,42 |
2,38 |
2,35 |
2,29 |
|
|
0,95 |
5,32 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,50 |
3,44 |
3,39 |
3,35 |
3,28 |
3,22 |
3,15 |
3,08 |
3,02 |
2,93 |
|
|
0,975 |
7,57 |
6,06 |
5,42 |
5,05 |
4,82 |
4,65 |
4,53 |
4,43 |
4,36 |
4,30 |
4,20 |
4,10 |
4,00 |
3,89 |
3,81 |
3,67 |
|
|
0,990 |
11,3 |
8,65 |
7,59 |
7,01 |
6,63 |
6,37 |
6,18 |
6,03 |
5,91 |
5,81 |
5,67 |
5,52 |
5,36 |
5,20 |
5,07 |
4,86 |
|
|
0,995 |
14,7 |
11,0 |
9,60 |
8,81 |
8,30 |
7,95 |
7,69 |
7,50 |
7,34 |
7,21 |
7,01 |
6,81 |
6,61 |
6,40 |
6,22 |
5,95 |
|
|
0,999 |
25,4 |
18,5 |
15,8 |
14,4 |
13,5 |
12,9 |
12,4 |
12,0 |
11,8 |
11,5 |
11,2 |
10,8 |
10,5 |
10,1 |
9,80 |
9,33 |
|
9 |
0,9 |
3,36 |
3,01 |
2,81 |
2,69 |
2,61 |
2,55 |
2,51 |
2,47 |
2,44 |
2,42 |
2,38 |
2,34 |
2,30 |
2,25 |
2,22 |
2,16 |
|
|
0,95 |
5,12 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,29 |
3,23 |
3,18 |
3,14 |
3,07 |
3,01 |
2,94 |
2,86 |
2,80 |
2,71 |
|
|
0,975 |
7,21 |
5,71 |
5,08 |
4,72 |
4,48 |
4,32 |
4,20 |
4,10 |
4,03 |
3,96 |
3,87 |
3,77 |
3,67 |
3,56 |
3,47 |
3,33 |
|
|
0,990 |
10,6 |
8,02 |
6,99 |
6,42 |
6,06 |
5,80 |
5,61 |
5,47 |
5,35 |
5,26 |
5,11 |
4,96 |
4,81 |
4,65 |
4,52 |
4,31 |
|
|
0,995 |
13,6 |
10,1 |
8,72 |
7,96 |
7,47 |
7,14 |
6,88 |
6,69 |
6,54 |
6,42 |
6,23 |
6,03 |
5,83 |
5,62 |
5,45 |
5,19 |
|
|
0,999 |
22,9 |
16,4 |
13,9 |
12,6 |
11,7 |
11,1 |
10,7 |
10,4 |
10,1 |
9,89 |
9,57 |
9,24 |
8,90 |
8,55 |
8,26 |
7,81 |
|
10 |
0,9 |
3,29 |
2,92 |
2,73 |
2,61 |
2,52 |
2,46 |
2,41 |
2,38 |
2,35 |
2,32 |
2,28 |
2,24 |
2,20 |
2,16 |
2,12 |
2,06 |
|
|
0,95 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,14 |
3,07 |
3,02 |
2,98 |
2,91 |
2,85 |
2,77 |
2,70 |
2,64 |
2,54 |
|
|
0,975 |
6,94 |
5,46 |
4,83 |
4,47 |
4,24 |
4,07 |
3,95 |
3,85 |
3,78 |
3,72 |
3,62 |
3,52 |
3,42 |
3,31 |
3,22 |
3,08 |
|
|
0,990 |
10,0 |
7,56 |
6,55 |
5,99 |
5,64 |
5,39 |
5,20 |
5,06 |
4,94 |
4,85 |
4,71 |
4,56 |
4,41 |
4,25 |
4,12 |
3,91 |
|
|
0,995 |
12,8 |
9,43 |
8,08 |
7,34 |
6,87 |
6,54 |
6,30 |
6,12 |
5,97 |
5,85 |
5,66 |
5,47 |
5,27 |
5,07 |
4,90 |
4,64 |
|
|
0,999 |
21,0 |
14,9 |
12,6 |
11,3 |
10,5 |
9,93 |
9,52 |
9,20 |
8,96 |
8,75 |
8,45 |
8,13 |
7,80 |
7,47 |
7,19 |
6,76 |
|
11 |
0,9 |
3,23 |
2,86 |
2,66 |
2,54 |
2,45 |
2,39 |
2,34 |
2,30 |
2,27 |
2,25 |
2,21 |
2,17 |
2,12 |
2,08 |
2,04 |
1,97 |
|
|
0,95 |
4,84 |
3,98 |
3,59 |
3,36 |
3,20 |
3,09 |
3,01 |
2,95 |
2,90 |
2,85 |
2,79 |
2,72 |
2,65 |
2,57 |
2,51 |
2,40 |
|
|
0,975 |
6,72 |
5,26 |
4,63 |
4,28 |
4,04 |
3,88 |
3,76 |
3,66 |
3,59 |
3,53 |
3,43 |
3,33 |
3,23 |
3,12 |
3,03 |
2,88 |
|
|
0,990 |
9,65 |
7,21 |
6,22 |
5,67 |
5,32 |
5,07 |
4,89 |
4,74 |
4,63 |
4,54 |
4,40 |
4,25 |
4,10 |
3,94 |
3,81 |
3,60 |
|
|
0,995 |
12,2 |
8,91 |
7,60 |
6,88 |
6,42 |
6,10 |
5,86 |
5,68 |
5,54 |
5,42 |
5,24 |
5,05 |
4,86 |
4,65 |
4,49 |
4,23 |
|
|
0,999 |
19,7 |
13,8 |
11,6 |
10,3 |
9,58 |
9,05 |
8,66 |
8,35 |
8,12 |
7,92 |
7,53 |
7,32 |
7,01 |
6,68 |
6,42 |
6,00 |
|
12 |
0,9 |
3,18 |
2,81 |
2,61 |
2,48 |
2,39 |
2,33 |
2,28 |
2,24 |
2,21 |
2,19 |
2,15 |
2,10 |
2,06 |
2,01 |
1,97 |
1,90 |
|
|
0,95 |
4,75 |
3,89 |
3,49 |
3,26 |
3,11 |
3,00 |
2,91 |
2,85 |
2,80 |
2,75 |
2,69 |
2,62 |
2,54 |
2,47 |
2,40 |
2,30 |
|
|
0,975 |
6,55 |
5,10 |
4,47 |
4,12 |
3,89 |
3,73 |
3,61 |
3,51 |
3,44 |
3,37 |
3,28 |
3,18 |
3,07 |
2,96 |
2,87 |
2,72 |
|
|
0,990 |
9,33 |
6,93 |
5,95 |
5,41 |
5,06 |
4,82 |
4,64 |
4,50 |
4,39 |
4,30 |
4,16 |
4,01 |
3,86 |
3,70 |
3,57 |
3,36 |
|
|
0,995 |
11,8 |
8,51 |
7,23 |
6,52 |
6,07 |
5,76 |
5,52 |
5,35 |
5,20 |
5,09 |
4,91 |
4,72 |
4,53 |
4,33 |
4,17 |
3,90 |
|
|
0,999 |
18,6 |
13,0 |
10,8 |
9,63 |
8,89 |
8,38 |
8,00 |
7,71 |
7,48 |
7,29 |
7,00 |
6,71 |
6,40 |
6,09 |
5,83 |
5,42 |
|
13 |
0,9 |
3,14 |
2,76 |
2,56 |
2,43 |
2,35 |
2,28 |
2,23 |
2,20 |
2,16 |
2,14 |
2,10 |
2,05 |
2,01 |
1,96 |
1,92 |
1,85 |
|
|
0,95 |
4,67 |
3,81 |
3,41 |
3,18 |
3,03 |
2,92 |
2,83 |
2,77 |
2,71 |
2,67 |
2,60 |
2,53 |
2,46 |
2,38 |
2,31 |
2,21 |
|
|
0,975 |
6,41 |
4,97 |
4,35 |
4,00 |
3,77 |
3,60 |
3,48 |
3,39 |
3,31 |
3,25 |
3,15 |
3,05 |
2,95 |
2,84 |
2,74 |
2,60 |
|
|
0,990 |
9,07 |
6,70 |
5,74 |
5,21 |
4,86 |
4,62 |
4,44 |
4,30 |
4,19 |
4,10 |
3,96 |
3,82 |
3,66 |
3,51 |
3,38 |
3,17 |
|
|
0,995 |
11,4 |
8,19 |
6,93 |
6,23 |
5,79 |
5,48 |
5,25 |
5,08 |
4,94 |
4,82 |
4,64 |
4,46 |
4,27 |
4,07 |
3,91 |
3,65 |
|
|
0,999 |
17,8 |
12,3 |
10,2 |
9,07 |
8,35 |
7,86 |
7,49 |
7,21 |
6,98 |
6,80 |
6,52 |
6,23 |
5,93 |
5,63 |
5,37 |
4,97 |
|
14 |
0,9 |
3,10 |
2,73 |
2,52 |
2,39 |
2,31 |
2,24 |
2,19 |
2,15 |
2,12 |
2,10 |
2,05 |
2,01 |
1,96 |
1,91 |
1,87 |
1,80 |
|
|
0,95 |
4,60 |
3,74 |
3,34 |
3,11 |
2,96 |
2,85 |
2,76 |
2,70 |
2,65 |
2,60 |
2,53 |
2,48 |
2,39 |
2,31 |
2,24 |
2,13 |
|
|
0,975 |
6,30 |
4,86 |
4,24 |
3,89 |
3,66 |
3,50 |
3,38 |
3,29 |
3,21 |
3,15 |
3,05 |
2,95 |
2,84 |
2,73 |
2,64 |
2,49 |
|
|
0,990 |
8,86 |
6,51 |
5,56 |
5,04 |
4,69 |
4,46 |
4,28 |
4,14 |
4,03 |
3,94 |
3,80 |
3,66 |
3,51 |
3,35 |
3,22 |
3,00 |
|
|
0,995 |
11,1 |
7,92 |
6,68 |
6,00 |
5,56 |
5,26 |
5,03 |
4,86 |
4,72 |
4,60 |
4,43 |
4,25 |
4,06 |
3,86 |
3,70 |
3,44 |
|
|
0,999 |
17,1 |
11,8 |
9,73 |
8,62 |
7,92 |
7,44 |
7,08 |
6,80 |
6,58 |
6,40 |
6,13 |
5,85 |
5,56 |
5,25 |
5,00 |
4,60 |
|
15 |
0,9 |
3,07 |
2,70 |
2,49 |
2,36 |
2,27 |
2,21 |
2,16 |
2,12 |
2,09 |
2,06 |
2,02 |
1,97 |
1,92 |
1,87 |
1,83 |
1,76 |
|
|
0,95 |
4,54 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,71 |
2,64 |
2,59 |
2,54 |
2,48 |
2,40 |
2,33 |
2,25 |
2,18 |
2,07 |
|
|
0,975 |
6,20 |
4,77 |
4,15 |
3,80 |
3,58 |
3,41 |
3,29 |
3,20 |
3,12 |
3,06 |
2,96 |
2,86 |
2,76 |
2,64 |
2,55 |
2,40 |
|
|
0,990 |
8,68 |
6,36 |
5,42 |
4,89 |
4,56 |
4,32 |
4,14 |
4,00 |
3,89 |
3,80 |
3,67 |
3,52 |
3,37 |
3,21 |
3,08 |
2,87 |
|
|
0,995 |
10,8 |
7,70 |
6,48 |
5,80 |
5,37 |
5,07 |
4,85 |
4,67 |
4,54 |
4,42 |
4,25 |
4,07 |
3,88 |
3,69 |
3,52 |
3,26 |
|
|
0,999 |
16,6 |
11,3 |
9,34 |
8,25 |
7,57 |
7,09 |
6,74 |
6,47 |
6,26 |
6,08 |
5,81 |
5,54 |
5,25 |
4,95 |
4,70 |
4,31 |
|
16 |
0,9 |
3,05 |
2,67 |
2,46 |
2,33 |
2,24 |
2,18 |
2,13 |
2,09 |
2,06 |
2,03 |
1,99 |
1,94 |
1,89 |
1,84 |
1,79 |
1,72 |
|
|
0,95 |
4,49 |
3,63 |
3,24 |
3,01 |
2,85 |
2,74 |
2,66 |
2,59 |
2,54 |
2,49 |
2,42 |
2,35 |
2,28 |
2,19 |
2,12 |
2,01 |
|
|
0,975 |
6,12 |
4,69 |
4,03 |
3,73 |
3,50 |
3,34 |
3,22 |
3,12 |
3,05 |
2,99 |
2,89 |
2,79 |
2,68 |
2,57 |
2,47 |
2,32 |
|
|
0,990 |
8,53 |
6,23 |
5,29 |
4,77 |
4,44 |
4,20 |
4,03 |
3,89 |
3,78 |
3,69 |
3,55 |
3,41 |
3,26 |
3,10 |
2,97 |
2,75 |
|
|
0,995 |
10,6 |
7,51 |
6,30 |
5,64 |
5,21 |
4,91 |
4,69 |
4,52 |
4,38 |
4,27 |
4,10 |
3,92 |
3,73 |
3,54 |
3,37 |
3,11 |
|
|
0,999 |
16,1 |
11,0 |
9,01 |
7,94 |
7,27 |
6,80 |
6,46 |
6,19 |
5,98 |
5,81 |
5,55 |
5,27 |
4,99 |
4,70 |
4,45 |
4,06 |
|
17 |
0,9 |
3,03 |
2,64 |
2,44 |
2,31 |
2,22 |
2,15 |
2,10 |
2,06 |
2,03 |
2,00 |
1,96 |
1,91 |
1,86 |
1,81 |
1,76 |
1,69 |
|
|
0,95 |
4,45 |
3,59 |
3,20 |
2,96 |
2,81 |
2,70 |
2,61 |
2,55 |
2,49 |
2,45 |
2,38 |
2,31 |
2,23 |
2,15 |
2,08 |
1,96 |
|
|
0,975 |
6,04 |
4,62 |
4,01 |
3,66 |
3,44 |
3,28 |
3,16 |
3,06 |
2,98 |
2,92 |
2,82 |
2,72 |
2,62 |
2,50 |
2,41 |
2,25 |
|
|
0,990 |
8,40 |
6,11 |
5,18 |
4,67 |
4,34 |
4,10 |
3,93 |
3,79 |
3,68 |
3,59 |
3,46 |
3,31 |
3,16 |
3,00 |
2,87 |
2,65 |
|
|
0,995 |
10,4 |
7,35 |
6,16 |
5,50 |
5,07 |
4,78 |
4,56 |
4,39 |
4,25 |
4,14 |
3,97 |
3,79 |
3,61 |
3,41 |
3,25 |
2,98 |
|
|
0,999 |
15,7 |
10,7 |
8,73 |
7,68 |
7,02 |
6,56 |
6,22 |
5,96 |
5,75 |
5,58 |
5,32 |
5,05 |
4,78 |
4,48 |
4,24 |
3,85 |
|
18 |
0,9 |
3,01 |
2,62 |
2,42 |
2,29 |
2,20 |
2,13 |
2,09 |
2,04 |
2,00 |
1,98 |
1,93 |
1,89 |
1,84 |
1,78 |
1,74 |
1,66 |
|
|
0,95 |
4,41 |
3,55 |
3,16 |
2,93 |
2,77 |
2,66 |
2,58 |
2,51 |
2,46 |
2,41 |
2,34 |
2,27 |
2,19 |
2,11 |
2,04 |
1,92 |
|
|
0,975 |
5,98 |
4,56 |
3,95 |
3,61 |
3,38 |
3,22 |
3,10 |
3,01 |
2,93 |
2,87 |
2,77 |
2,67 |
2,56 |
2,44 |
2,35 |
2,19 |
|
|
0,990 |
8,29 |
6,01 |
5,09 |
4,58 |
4,25 |
4,01 |
3,94 |
3,71 |
3,60 |
3,51 |
3,37 |
3,23 |
3,08 |
2,92 |
2,78 |
2,57 |
|
|
0,995 |
10,2 |
7,21 |
6,03 |
5,37 |
4,96 |
4,66 |
4,44 |
4,28 |
4,14 |
4,03 |
3,86 |
3,68 |
3,50 |
3,30 |
3,14 |
2,87 |
|
|
0,999 |
15,4 |
10,4 |
8,49 |
7,46 |
6,81 |
6,35 |
6,02 |
5,76 |
5,56 |
5,39 |
5,13 |
4,87 |
4,59 |
4,30 |
4,06 |
3,67 |
|
19 |
0,9 |
2,99 |
2,61 |
2,40 |
2,27 |
2,18 |
2,11 |
2,06 |
2,02 |
1,98 |
1,96 |
1,91 |
1,86 |
1,81 |
1,76 |
1,71 |
1,63 |
|
|
0,95 |
4,38 |
3,52 |
3,13 |
2,90 |
2,74 |
2,63 |
2,54 |
2,48 |
2,42 |
2,38 |
2,31 |
2,23 |
2,16 |
2,07 |
2,00 |
1,88 |
|
|
0,975 |
5,92 |
4,51 |
3,90 |
3,56 |
3,33 |
3,17 |
3,05 |
2,96 |
2,88 |
2,82 |
2,72 |
2,62 |
2,51 |
2,39 |
2,30 |
2,13 |
|
|
0,990 |
8,18 |
5,93 |
5,01 |
4,50 |
4,17 |
3,94 |
3,77 |
3,63 |
3,52 |
3,43 |
3,30 |
3,15 |
3,00 |
2,84 |
2,71 |
2,49 |
|
|
0,995 |
10,1 |
7,09 |
5,92 |
5,27 |
4,85 |
4,56 |
4,34 |
4,18 |
4,04 |
3,93 |
3,76 |
3,59 |
3,40 |
3,21 |
3,04 |
2,78 |
|
|
0,999 |
15,1 |
10,2 |
8,28 |
7,27 |
6,62 |
6,18 |
5,85 |
5,59 |
5,39 |
5,22 |
4,97 |
4,70 |
4,43 |
4,14 |
3,90 |
3,51 |
|
20 |
0,9 |
2,97 |
2,59 |
2,38 |
2,25 |
2,16 |
2,09 |
2,04 |
2,00 |
1,96 |
1,94 |
1,89 |
1,84 |
1,79 |
1,74 |
1,69 |
1,61 |
|
|
0,95 |
4,35 |
3,49 |
3,10 |
2,87 |
2,71 |
2,60 |
2,51 |
2,45 |
2,39 |
2,35 |
2,28 |
2,20 |
2,12 |
2,04 |
1,97 |
1,84 |
|
|
0,975 |
5,87 |
4,46 |
3,86 |
3,51 |
3,29 |
3,13 |
3,01 |
2,91 |
2,84 |
2,77 |
2,68 |
2,57 |
2,46 |
2,35 |
2,25 |
2,09 |
|
|
0,990 |
8,10 |
5,85 |
4,94 |
4,43 |
4,10 |
3,87 |
3,70 |
3,56 |
3,46 |
3,37 |
3,23 |
3,09 |
2,94 |
2,78 |
2,64 |
2,42 |
|
|
0,995 |
9,94 |
6,99 |
5,82 |
5,17 |
4,76 |
4,47 |
4,26 |
4,09 |
3,96 |
3,85 |
3,68 |
3,50 |
3,32 |
3,12 |
2,96 |
2,69 |
|
|
0,999 |
14,8 |
9,95 |
8,10 |
7,10 |
6,46 |
6,02 |
5,69 |
5,44 |
5,24 |
5,08 |
4,82 |
4,56 |
4,29 |
4,00 |
3,77 |
3,38 |
|
21 |
0,9 |
2,96 |
2,57 |
2,36 |
2,23 |
2,14 |
2,08 |
2,02 |
1,98 |
1,95 |
1,92 |
1,87 |
1,83 |
1,78 |
1,72 |
1,67 |
1,59 |
|
|
0,95 |
4,32 |
3,47 |
3,07 |
2,84 |
2,68 |
2,57 |
2,49 |
2,42 |
2,37 |
2,32 |
2,25 |
2,18 |
2,10 |
2,01 |
1,94 |
1,81 |
|
|
0,975 |
5,83 |
4,42 |
3,82 |
3,48 |
3,25 |
3,09 |
2,97 |
2,87 |
2,80 |
2,73 |
2,64 |
2,53 |
2,42 |
2,31 |
2,21 |
2,04 |
|
|
0,990 |
8,02 |
5,78 |
4,87 |
4,37 |
4,04 |
3,81 |
3,64 |
3,51 |
3,40 |
3,31 |
3,17 |
3,03 |
2,88 |
2,72 |
2,58 |
2,36 |
|
|
0,995 |
9,83 |
6,89 |
5,73 |
5,09 |
4,68 |
4,39 |
4,18 |
4,01 |
3,88 |
3,77 |
3,60 |
3,43 |
3,24 |
3,05 |
2,88 |
2,61 |
|
|
0,999 |
14,6 |
9,77 |
7,94 |
6,95 |
6,32 |
5,88 |
5,56 |
5,31 |
5,11 |
4,95 |
4,70 |
4,44 |
4,17 |
3,88 |
3,64 |
3,26 |
|
22 |
0,9 |
2,95 |
2,56 |
2,35 |
2,22 |
2,13 |
2,06 |
2,01 |
1,97 |
1,93 |
1,90 |
1,86 |
1,81 |
1,76 |
1,70 |
1,65 |
1,57 |
|
|
0,95 |
4,30 |
3,44 |
3,05 |
2,82 |
2,66 |
2,55 |
2,46 |
2,40 |
2,34 |
2,30 |
2,23 |
2,15 |
2,07 |
1,98 |
1,91 |
1,78 |
|
|
0,975 |
5,79 |
4,38 |
3,78 |
3,44 |
3,22 |
3,05 |
2,93 |
2,84 |
2,76 |
2,70 |
2,60 |
2,50 |
2,39 |
2,27 |
2,17 |
2,00 |
|
|
0,990 |
7,95 |
5,72 |
4,82 |
4,31 |
3,99 |
3,76 |
3,59 |
3,45 |
3,35 |
3,26 |
3,12 |
2,98 |
2,83 |
2,67 |
2,53 |
2,31 |
|
|
0,995 |
9,73 |
6,81 |
5,65 |
5,02 |
4,61 |
4,32 |
4,11 |
3,94 |
3,81 |
3,70 |
3,54 |
3,36 |
3,18 |
2,98 |
2,82 |
2,55 |
|
|
0,999 |
14,4 |
9,61 |
7,80 |
6,81 |
6,19 |
5,76 |
5,44 |
5,19 |
4,99 |
4,83 |
4,58 |
4,33 |
4,06 |
3,78 |
3,54 |
3,15 |
|
23 |
0,9 |
2,94 |
2,55 |
2,34 |
2,21 |
2,11 |
2,05 |
1,99 |
1,95 |
1,92 |
1,89 |
1,84 |
1,80 |
1,74 |
1,69 |
1,64 |
1,55 |
|
|
0,95 |
4,28 |
3,42 |
3,03 |
2,80 |
2,64 |
2,53 |
2,44 |
2,37 |
2,32 |
2,27 |
2,20 |
2,13 |
2,05 |
1,96 |
1,88 |
1,76 |
|
|
0,975 |
5,75 |
4,35 |
3,75 |
3,41 |
3,18 |
3,02 |
2,90 |
2,81 |
2,73 |
2,67 |
2,57 |
2,47 |
2,36 |
2,24 |
2,14 |
1,97 |
|
|
0,990 |
7,88 |
5,66 |
4,76 |
4,26 |
3,94 |
3,71 |
3,54 |
3,41 |
3,30 |
3,21 |
3,07 |
2,93 |
2,78 |
2,62 |
2,48 |
2,26 |
|
|
0,995 |
9,63 |
6,73 |
5,58 |
4,95 |
4,54 |
4,26 |
4,05 |
3,88 |
3,75 |
3,64 |
3,47 |
3,30 |
3,12 |
2,92 |
2,76 |
2,48 |
|
|
0,999 |
14,2 |
9,47 |
7,64 |
6,70 |
6,08 |
5,65 |
5,33 |
5,09 |
4,89 |
4,73 |
4,48 |
4,23 |
3,96 |
3,68 |
3,44 |
3,05 |
|
24 |
0,9 |
2,93 |
2,54 |
2,33 |
2,19 |
2,10 |
2,04 |
1,98 |
1,94 |
1,91 |
1,88 |
1,83 |
1,78 |
1,73 |
1,67 |
1,62 |
1,53 |
|
|
0,95 |
4,26 |
3,40 |
3,01 |
2,78 |
2,62 |
2,51 |
2,42 |
2,36 |
2,30 |
2,25 |
2,18 |
2,11 |
2,03 |
1,94 |
1,86 |
1,73 |
|
|
0,975 |
5,72 |
4,32 |
3,72 |
3,38 |
3,15 |
2,99 |
2,87 |
2,78 |
2,70 |
2,64 |
2,54 |
2,44 |
2,33 |
2,21 |
2,11 |
1,94 |
|
|
0,990 |
7,82 |
5,61 |
4,72 |
4,22 |
3,90 |
3,67 |
3,50 |
3,36 |
3,26 |
3,17 |
3,03 |
2,89 |
2,74 |
2,58 |
2,44 |
2,21 |
|
|
0,995 |
9,55 |
6,66 |
5,52 |
4,89 |
4,49 |
4,20 |
3,99 |
3,83 |
3,69 |
3,59 |
3,42 |
3,25 |
3,06 |
2,87 |
2,70 |
2,43 |
|
|
0,999 |
14,0 |
9,34 |
7,55 |
6,59 |
5,98 |
5,55 |
5,23 |
4,99 |
4,80 |
4,64 |
4,39 |
4,14 |
3,87 |
3,59 |
3,36 |
2,97 |
|
25 |
0,9 |
2,92 |
2,53 |
2,32 |
2,18 |
2,09 |
2,02 |
1,97 |
1,93 |
1,89 |
1,87 |
1,82 |
1,77 |
1,72 |
1,56 |
1,61 |
1,52 |
|
|
0,95 |
4,24 |
3,39 |
2,99 |
2,76 |
2,60 |
2,49 |
2,40 |
2,34 |
2,28 |
2,24 |
2,16 |
2,09 |
2,01 |
1,92 |
1,84 |
1,71 |
|
|
0,975 |
5,69 |
4,29 |
3,69 |
3,35 |
3,13 |
2,97 |
2,85 |
2,75 |
2,68 |
2,61 |
2,51 |
2,41 |
2,30 |
2,18 |
2,08 |
1,91 |
|
|
0,990 |
7,77 |
5,57 |
4,68 |
4,18 |
3,85 |
3,63 |
3,46 |
3,32 |
3,22 |
3,13 |
2,99 |
2,85 |
2,70 |
2,54 |
2,40 |
2,17 |
|
|
0995 |
9,48 |
6,60 |
5,46 |
4,84 |
4,43 |
4,15 |
3,94 |
3,78 |
3,64 |
3,54 |
3,37 |
3,20 |
3,01 |
2,82 |
2,65 |
2,38 |
|
|
0,999 |
13,9 |
9,22 |
7,45 |
6,49 |
5,89 |
5,46 |
5,15 |
4,91 |
4,71 |
4,56 |
4,31 |
4,06 |
3,79 |
3,52 |
3,28 |
2,89 |
|
30 |
0,9 |
2,88 |
2,49 |
2,28 |
2,14 |
2,05 |
1,98 |
1,93 |
1,88 |
1,85 |
1,82 |
1,77 |
1,72 |
1,67 |
1,61 |
1,55 |
1,46 |
|
|
0,95 |
4,17 |
3,32 |
2,92 |
2,69 |
2,53 |
2,42 |
2,33 |
2,27 |
2,21 |
2,16 |
2,09 |
2,01 |
1,93 |
1,84 |
1,76 |
1,62 |
|
|
0,975 |
5,57 |
4,18 |
3,59 |
3,25 |
3,03 |
2,87 |
2,75 |
2,65 |
2,57 |
2,51 |
2,41 |
2,31 |
2,20 |
2,07 |
1,97 |
1,79 |
|
|
0,990 |
7,56 |
5,39 |
4,51 |
4,02 |
3,70 |
3,47 |
3,30 |
3,17 |
3,07 |
2,98 |
2,84 |
2,70 |
2,55 |
2,39 |
2,25 |
2,01 |
|
|
0,995 |
9,18 |
6,35 |
5,24 |
4,82 |
4,23 |
3,95 |
3,74 |
3,58 |
3,45 |
3,34 |
3,18 |
3,01 |
2,82 |
2,63 |
2,46 |
2,18 |
|
|
0,999 |
13,3 |
8,77 |
7,05 |
6,12 |
5,53 |
5,12 |
4,82 |
4,58 |
4,39 |
4,24 |
4,00 |
3,75 |
3,49 |
3,22 |
2,98 |
2,59 |
|
35 |
0,9 |
2,85 |
2,46 |
2,25 |
2,11 |
2,02 |
1,95 |
1,90 |
1,85 |
1,82 |
1,79 |
1,74 |
1,69 |
1,63 |
1,57 |
1,51 |
1,41 |
|
|
0,95 |
4,12 |
3,27 |
2,87 |
2,64 |
2,49 |
2,37 |
2,29 |
2,22 |
2,16 |
2,11 |
2,04 |
1,96 |
1,88 |
1,79 |
1,70 |
1,56 |
|
|
0,975 |
5,48 |
4,11 |
3,52 |
3,18 |
2,96 |
2,80 |
2,68 |
2,58 |
2,50 |
2,44 |
2,34 |
2,23 |
2,12 |
2,00 |
1,89 |
1,70 |
|
|
0,990 |
7,42 |
5,27 |
4,40 |
3,91 |
3,59 |
3,37 |
3,20 |
3,07 |
2,96 |
2,88 |
2,74 |
2,60 |
2,44 |
2,28 |
2,14 |
1,89 |
|
|
0,995 |
8,98 |
6,19 |
5,39 |
4,48 |
4,09 |
3,81 |
3,61 |
3,45 |
3,32 |
3,21 |
3,05 |
2,88 |
2,69 |
2,50 |
2,33 |
2,04 |
|
|
0,999 |
10,9 |
8,47 |
6,79 |
5,88 |
5,30 |
4,89 |
4,59 |
4,36 |
4,18 |
4,03 |
3,79 |
3,55 |
3,29 |
3,02 |
2,78 |
2,38 |
|
40 |
0,9 |
2,84 |
2,44 |
2,23 |
2,09 |
2,00 |
1,93 |
1,87 |
1,83 |
1,79 |
1,76 |
1,71 |
1,66 |
1,61 |
1,54 |
1,48 |
1,38 |
|
|
0,95 |
4,08 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,25 |
2,18 |
2,12 |
2,08 |
2,00 |
1,92 |
1,84 |
1,74 |
1,66 |
1,51 |
|
|
0,975 |
5,42 |
4,05 |
3,46 |
3,13 |
2,90 |
2,74 |
2,62 |
2,53 |
2,45 |
2,39 |
2,29 |
2,18 |
2,07 |
1,94 |
1,83 |
1,64 |
|
|
0,990 |
7,31 |
5,18 |
4,31 |
3,83 |
3,51 |
3,29 |
3,12 |
2,99 |
2,89 |
2,80 |
2,66 |
2,52 |
2,37 |
2,20 |
2,06 |
1,80 |
|
|
0,995 |
8,83 |
6,07 |
4,98 |
4,37 |
3,99 |
3,71 |
3,51 |
3,35 |
3,22 |
3,12 |
2,95 |
2,78 |
2,60 |
2,40 |
2,23 |
1,93 |
|
|
0,999 |
12,6 |
8,25 |
6,59 |
5,70 |
5,13 |
4,73 |
4,44 |
4,21 |
4,02 |
3,87 |
3,64 |
3,40 |
3,14 |
2,87 |
2,64 |
2,23 |
|
45 |
0,9 |
2,82 |
2,42 |
2,21 |
2,07 |
1,98 |
1,91 |
1,85 |
1,81 |
1,77 |
1,74 |
1,70 |
1,64 |
1,58 |
1,52 |
1,46 |
1,35 |
|
|
0,95 |
4,06 |
3,20 |
2,81 |
2,58 |
2,42 |
2,31 |
2,22 |
2,15 |
2,10 |
2,05 |
1,97 |
1,89 |
1,81 |
1,71 |
1,63 |
1,47 |
|
|
0,975 |
5,38 |
4,01 |
3,42 |
3,09 |
2,86 |
2,70 |
2,58 |
2,49 |
2,41 |
2,35 |
2,25 |
2,14 |
2,03 |
1,90 |
1,79 |
1,59 |
|
|
0,990 |
7,23 |
5,11 |
4,25 |
3,77 |
3,45 |
3,23 |
3,07 |
2,94 |
2,83 |
2,74 |
2,61 |
2,46 |
2,31 |
2,14 |
2,00 |
1,74 |
|
|
0,995 |
8,71 |
5,97 |
4,89 |
4,29 |
3,91 |
3,64 |
3,43 |
3,28 |
3,15 |
3,04 |
2,88 |
2,71 |
2,53 |
2,33 |
2,16 |
1,85 |
|
|
9,999 |
12,4 |
8,09 |
6,45 |
5,56 |
5,00 |
4,61 |
4,32 |
4,09 |
3,91 |
3,76 |
3,53 |
3,29 |
3,04 |
2,76 |
2,53 |
2,12 |
|
50 |
0,9 |
2,81 |
2,41 |
2,20 |
2,06 |
1,97 |
1,90 |
1,84 |
1,80 |
1,76 |
1,73 |
1,68 |
1,63 |
1,57 |
1,50 |
1,44 |
1,33 |
|
|
0,95 |
4,03 |
3,18 |
2,79 |
2,56 |
2,40 |
2,29 |
2,20 |
2,13 |
2,07 |
2,03 |
1,95 |
1,87 |
1,78 |
1,69 |
1,60 |
1,44 |
|
|
0,975 |
5,34 |
3,97 |
3,39 |
3,05 |
2,83 |
2,67 |
2,55 |
2,46 |
2,38 |
2,32 |
2,22 |
2,11 |
1,99 |
1,87 |
1,75 |
1,55 |
|
|
0,990 |
7,17 |
5,06 |
4,20 |
3,72 |
3,41 |
3,19 |
3,02 |
2,89 |
2,78 |
2,70 |
2,56 |
2,42 |
2,27 |
2,10 |
1,95 |
1,68 |
|
|
0,995 |
8,63 |
5,90 |
4,83 |
4,23 |
3,85 |
3,58 |
3,38 |
3,22 |
3,09 |
2,99 |
2,82 |
2,65 |
2,47 |
2,27 |
2,10 |
1,79 |
|
|
0,999 |
12,2 |
7,96 |
6,34 |
5,46 |
4,90 |
4,51 |
4,22 |
4,00 |
3,82 |
3,67 |
3,44 |
3,20 |
2,95 |
2,68 |
2,44 |
2,03 |
|
60 |
0,9 |
2,79 |
2,39 |
2,18 |
2,04 |
1,95 |
1,87 |
1,82 |
1,77 |
1,74 |
1,71 |
1,66 |
1,60 |
1,54 |
1,48 |
1,41 |
1,29 |
|
|
0,95 |
4,00 |
3,15 |
2,76 |
2,53 |
2,37 |
2,25 |
2,17 |
2,10 |
2,04 |
1,99 |
1,92 |
1,84 |
1,75 |
1,65 |
1,56 |
1,39 |
|
|
0,975 |
5,29 |
3,93 |
3,34 |
3,01 |
2,79 |
2,63 |
2,51 |
2,41 |
2,33 |
2,27 |
2,17 |
2,06 |
1,94 |
1,82 |
1,70 |
1,48 |
|
|
0,990 |
7,08 |
4,98 |
4,13 |
3,65 |
3,34 |
3,12 |
2,95 |
2,82 |
2,72 |
2,63 |
2,50 |
2,35 |
2,20 |
2,03 |
1,88 |
1,60 |
|
|
0,995 |
8,49 |
5,79 |
4,73 |
4,14 |
3,76 |
3,49 |
3,29 |
3,13 |
3,01 |
2,90 |
2,74 |
2,57 |
2,39 |
2,19 |
2,01 |
1,69 |
|
|
0,999 |
12,0 |
7,77 |
6,17 |
5,31 |
4,76 |
4,37 |
4,09 |
3,86 |
3,69 |
3,54 |
3,32 |
3,08 |
2,83 |
2,55 |
2,32 |
1,89 |
|
80 |
0,9 |
2,77 |
2,37 |
2,15 |
2,02 |
1,92 |
1,85 |
1,79 |
1,75 |
1,71 |
1,68 |
1,63 |
1,57 |
1,51 |
1,44 |
1,38 |
1,24 |
|
|
0,95 |
3,96 |
3,11 |
2,72 |
2,49 |
2,33 |
2,21 |
2,13 |
2,06 |
2,00 |
1,95 |
1,88 |
1,79 |
1,70 |
1,60 |
1,51 |
1,32 |
|
|
0,975 |
5,22 |
3,86 |
3,28 |
2,95 |
2,73 |
2,57 |
2,45 |
2,35 |
2,28 |
2,21 |
2,11 |
2,00 |
1,88 |
1,75 |
1,63 |
1,40 |
|
|
0,990 |
6,96 |
4,88 |
4,04 |
3,56 |
3,26 |
3,04 |
2,87 |
2,74 |
2,64 |
2,55 |
2,42 |
2,27 |
2,12 |
1,94 |
1,79 |
1,49 |
|
|
0,995 |
8,33 |
5,67 |
4,61 |
4,03 |
3,65 |
3,39 |
3,19 |
3,03 |
2,91 |
2,80 |
2,64 |
2,47 |
2,29 |
2,08 |
1,90 |
1,56 |
|
|
0,999 |
11,7 |
7,54 |
5,97 |
5,12 |
4,58 |
4,20 |
3,92 |
3,70 |
3,53 |
3,39 |
3,16 |
2,93 |
2,68 |
2,41 |
2,16 |
1,72 |
|
100 |
0,9 |
2,76 |
2,36 |
2,14 |
2,00 |
1,91 |
1,83 |
1,78 |
1,73 |
1,69 |
1,66 |
1,61 |
1,56 |
1,49 |
1,42 |
1,35 |
1,21 |
|
|
0,95 |
3,94 |
3,09 |
2,70 |
2,46 |
2,31 |
2,19 |
2,10 |
2,03 |
1,97 |
1,93 |
1,85 |
1,77 |
1,68 |
1,57 |
1,48 |
1,28 |
|
|
0,975 |
5,18 |
3,83 |
3,25 |
2,92 |
2,70 |
2,54 |
2,42 |
2,32 |
2,24 |
2,18 |
2,08 |
1,97 |
1,85 |
1,71 |
1,59 |
1,35 |
|
|
0,990 |
6,90 |
4,82 |
3,98 |
3,51 |
3,21 |
2,99 |
2,82 |
2,69 |
2,59 |
2,50 |
2,37 |
2,22 |
2,07 |
1,89 |
1,74 |
1,43 |
|
|
0,995 |
8,24 |
5,59 |
4,54 |
3,96 |
3,59 |
3,33 |
3,13 |
2,97 |
2,85 |
2,74 |
2,58 |
2,41 |
2,23 |
2,02 |
1,84 |
1,49 |
|
|
0,999 |
11,5 |
7,41 |
5,86 |
5,02 |
4,48 |
4,11 |
3,83 |
3,61 |
3,44 |
3,30 |
3,07 |
2,84 |
2,59 |
2,32 |
2,08 |
1,62 |
|
120 |
0,9 |
2,75 |
2,35 |
2,13 |
1,99 |
1,90 |
1,82 |
1,77 |
1,72 |
1,68 |
1,65 |
1,60 |
1,55 |
1,48 |
1,41 |
1,34 |
1,19 |
|
|
0,95 |
3,92 |
3,07 |
2,68 |
2,45 |
2,29 |
2,18 |
2,09 |
2,02 |
1,96 |
1,91 |
1,83 |
1,75 |
1,66 |
1,55 |
1,46 |
1,25 |
|
|
0,975 |
5,15 |
3,80 |
3,23 |
2,89 |
2,67 |
2,52 |
2,39 |
2,30 |
2,22 |
2,16 |
2,05 |
1,94 |
1,82 |
1,69 |
1,56 |
1,31 |
|
|
0,990 |
6,85 |
4,79 |
3,95 |
3,48 |
3,17 |
2,96 |
2,79 |
2,66 |
2,56 |
2,47 |
2,34 |
2,19 |
2,03 |
1,86 |
1,70 |
1,38 |
|
|
0,995 |
8,18 |
5,54 |
4,50 |
3,92 |
3,55 |
3,28 |
3,09 |
2,93 |
2,81 |
2,71 |
2,54 |
2,37 |
2,19 |
1,98 |
1,80 |
1,43 |
|
|
0,999 |
11,4 |
7,32 |
5,78 |
4,95 |
4,42 |
4,04 |
3,77 |
3,55 |
3,38 |
3,24 |
3,02 |
2,78 |
2,53 |
2,26 |
2,02 |
1,54 |
|
¥ |
0,9 |
2,71 |
2,30 |
2,08 |
1,94 |
1,85 |
1,77 |
1,72 |
1,67 |
1,63 |
1,60 |
1,55 |
1,49 |
1,42 |
1,34 |
1,26 |
1,00 |
|
|
0,95 |
3,84 |
3,00 |
2,60 |
2,37 |
2,21 |
2,10 |
2,01 |
1,94 |
1,88 |
1,83 |
1,75 |
1,67 |
1,57 |
1,46 |
1,35 |
1,00 |
|
|
0,975 |
5,02 |
3,69 |
3,12 |
2,79 |
2,57 |
2,41 |
2,29 |
2,19 |
2,11 |
2,05 |
1,94 |
1,83 |
1,71 |
1,57 |
1,43 |
1,00 |
|
|
0,990 |
6,63 |
4,61 |
3,78 |
3,32 |
3,02 |
2,80 |
2,64 |
2,51 |
2,41 |
2,32 |
2,18 |
2,04 |
1,88 |
1,70 |
1,52 |
1,00 |
|
|
0,995 |
7,88 |
5,30 |
4,28 |
3,72 |
3,35 |
3,09 |
2,90 |
2,74 |
2,62 |
2,52 |
2,36 |
2,19 |
2,00 |
1,79 |
1,59 |
1,00 |
|
|
0,999 |
10,8 |
6,91 |
5,42 |
4,62 |
4,10 |
3,74 |
3,47 |
3,27 |
3,10 |
2,96 |
2,74 |
2,51 |
2,27 |
1,99 |
1,73 |
1,00 |
|
Примечание - Fa (f1, f2) = 1/F1-a(f2, f1) |
|||||||||||||||||
Таблица 5 - Общий объем двух выборок п1 = п2 для обеспечения заданной мощности 1 - b (0,9; 0,8 или 0,5) при проверке гипотезы Н0: р1 £ р2 для a = 0,05 и различных значений р1 и р2 при условии, что р1 > р2
|
р2 |
р1 |
|||||||||
|
0,95 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,4 |
0,3 |
0,2 |
0,1 |
|
|
0,9 |
503 |
|
|
|
|
|
|
|
|
|
|
|
371 |
|
|
|
|
|
|
|
|
|
|
|
184 |
|
|
|
|
|
|
|
|
|
|
0,8 |
89 |
232 |
|
|
|
|
|
|
|
|
|
|
67 |
173 |
|
|
|
|
|
|
|
|
|
|
38 |
87 |
|
|
|
|
|
|
|
|
|
0,7 |
42 |
74 |
338 |
|
|
|
|
|
|
|
|
|
34 |
56 |
249 |
|
|
|
|
|
|
|
|
|
19 |
31 |
121 |
|
|
|
|
|
|
|
|
0,6 |
25 |
39 |
97 |
408 |
|
|
|
|
|
|
|
|
20 |
30 |
73 |
302 |
|
|
|
|
|
|
|
|
12 |
17 |
37 |
143 |
|
|
|
|
|
|
|
0,5 |
18 |
25 |
47 |
111 |
445 |
|
|
|
|
|
|
|
14 |
19 |
36 |
84 |
321 |
|
|
|
|
|
|
|
9 |
11 |
19 |
43 |
155 |
|
|
|
|
|
|
0,4 |
13 |
17 |
30 |
53 |
116 |
445 |
|
|
|
|
|
|
11 |
13 |
23 |
41 |
85 |
321 |
|
|
|
|
|
|
7 |
9 |
12 |
22 |
43 |
155 |
|
|
|
|
|
0,3 |
10 |
12 |
18 |
31 |
53 |
111 |
408 |
|
|
|
|
|
9 |
10 |
15 |
23 |
41 |
84 |
302 |
|
|
|
|
|
6 |
6 |
9 |
12 |
22 |
43 |
143 |
|
|
|
|
0,2 |
8 |
10 |
12 |
18 |
30 |
47 |
97 |
338 |
|
|
|
|
6 |
8 |
10 |
15 |
23 |
36 |
73 |
249 |
|
|
|
|
5 |
5 |
6 |
9 |
12 |
19 |
37 |
121 |
|
|
|
0,1 |
6 |
8 |
10 |
12 |
17 |
25 |
39 |
74 |
232 |
|
|
|
5 |
6 |
8 |
10 |
13 |
19 |
30 |
56 |
173 |
|
|
|
3 |
3 |
5 |
6 |
9 |
11 |
17 |
31 |
87 |
|
|
0,05 |
5 |
6 |
8 |
10 |
13 |
18 |
25 |
42 |
89 |
503 |
|
|
5 |
5 |
6 |
9 |
11 |
14 |
20 |
34 |
67 |
371 |
|
|
3 |
3 |
5 |
6 |
7 |
9 |
12 |
19 |
38 |
184 |
|
Примечание - В каждой ячейке таблицы верхнее число обозначает общий объем выборки п1 = n2 для 1 - b = 0,9, среднее число соответствует 1 - b = 0,8, а нижнее число соответствует 1 - b = 0,5. Например, если р1 = 0,9 и р2 = 0,8, нужно выбрать п1 = n2 = 232 для 1 - b = 0,9, п1 = n2 = 173 для 1 - b = 0,8 и п1 = n2 = 87 для 1 - b = 0,5. |
||||||||||
Таблица 6 - Общий размер двух выборок п1 = п2 для обеспечения заданной мощности 1 - b (0,9; 0,8 или 0,5) при проверке гипотезы Н0: р1 £ р2 для a = 0,01 и различных значений р1 и р2 при условии, что р1 > р2
|
р2 |
р1 |
|||||||||
|
0,95 |
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
0,4 |
0,3 |
0,2 |
0,2 |
|
|
0,9 |
745 |
|
|
|
|
|
|
|
|
|
|
|
583 |
|
|
|
|
|
|
|
|
|
|
|
333 |
|
|
|
|
|
|
|
|
|
|
0,8 |
130 |
344 |
|
|
|
|
|
|
|
|
|
|
101 |
269 |
|
|
|
|
|
|
|
|
|
|
61 |
155 |
|
|
|
|
|
|
|
|
|
0,7 |
60 |
108 |
503 |
|
|
|
|
|
|
|
|
|
49 |
86 |
393 |
|
|
|
|
|
|
|
|
|
32 |
52 |
221 |
|
|
|
|
|
|
|
|
0,6 |
37 |
56 |
143 |
609 |
|
|
|
|
|
|
|
|
31 |
46 |
113 |
475 |
|
|
|
|
|
|
|
|
18 |
27 |
66 |
265 |
|
|
|
|
|
|
|
0,5 |
25 |
35 |
69 |
163 |
667 |
|
|
|
|
|
|
|
20 |
29 |
55 |
129 |
519 |
|
|
|
|
|
|
|
14 |
18 |
34 |
73 |
285 |
|
|
|
|
|
|
0,4 |
18 |
24 |
42 |
77 |
171 |
667 |
|
|
|
|
|
|
16 |
20 |
34 |
60 |
137 |
519 |
|
|
|
|
|
|
10 |
13 |
21 |
35 |
78 |
285 |
|
|
|
|
|
0,3 |
14 |
18 |
28 |
43 |
77 |
163 |
609 |
|
|
|
|
|
12 |
15 |
22 |
35 |
60 |
129 |
475 |
|
|
|
|
|
9 |
10 |
13 |
22 |
35 |
73 |
265 |
|
|
|
|
0,2 |
12 |
13 |
18 |
28 |
42 |
69 |
143 |
503 |
|
|
|
|
9 |
12 |
16 |
22 |
34 |
55 |
113 |
393 |
|
|
|
|
6 |
8 |
9 |
13 |
21 |
34 |
66 |
221 |
|
|
|
0,1 |
9 |
9 |
13 |
18 |
24 |
35 |
56 |
108 |
344 |
|
|
|
8 |
9 |
12 |
15 |
20 |
29 |
46 |
86 |
269 |
|
|
|
6 |
6 |
8 |
10 |
13 |
18 |
27 |
52 |
155 |
|
|
0,05 |
8 |
9 |
12 |
14 |
18 |
25 |
37 |
60 |
130 |
745 |
|
|
5 |
8 |
9 |
12 |
16 |
20 |
31 |
49 |
101 |
583 |
|
|
5 |
6 |
6 |
9 |
10 |
14 |
18 |
32 |
61 |
333 |
|
Примечание - В каждой ячейке таблицы верхнее число обозначает общий объем выборки п1 = n2 для 1 - b = 0,9, среднее число соответствует 1 - b = 0,8, а нижнее число соответствует 1 - b = 0,5. Например, если р1 = 0,9 и р2 = 0,8, нужно выбрать п1 = n2 = 344 для 1 - b = 0,9 и п1 = n2 = 155 для 1 - b = 0,5. |
||||||||||

Рисунок 2 - Номограмма Ларсона для биномиального распределения
Примечание - Если р < 0,01, необходимо отметить lр вместо р на шкале р и умножить значение, указанное на n-шкале, на l. Определить l как 0,01/р, округляя до ближайшего большего целого значения.
Приложение А (обязательное)
Вычисление оперативной характеристики критерия для формы В
А.1 Односторонний критерий для Н0: р ³ р0
|
Характеристика: |
|
Процедура определения: |
|
Элементы: |
|
Критерий для идентификации целевых элементов: |
|
Примечания: |
|
Заданное значение р0 = |
|
Выбранный уровень значимости a = |
|
Объем выборки п = |
|
Пропорция, для которой рассчитывается вероятность неотклонения гипотезы Н0 - р' = |
|
Если критические значения, соответствующие п и р0 для указанного уровня значимости a, неизвестны, они должны быть вычислены по 8.2 (формы В). |
|
Cl,0 = |
|
Определение вероятности неотклонения нулевой гипотезы Н0 - Рa. |
|
Если гипотеза Н0 истинна, то вероятность ошибки первого рода равна 1 - Рa. Достигнутый уровень значимости a' равен вероятности ошибки первого рода при р' = р0. |
|
Если альтернативная гипотеза истинна, вероятность ошибки второго рода равна Рa. |
|
|
|
По таблице 3 определяют: |
|
Ф(и') = |
|
Результаты вычислений: |
|
Рa = 1 - Ф(и') = |
|
р' = р0 - a'= Ф(и') = |
|
р' < р0 - b = 1 - Ф(и') = |
А.2 Односторонний критерий для Н0: р £ р0
|
Характеристика: |
|
Процедура определения: |
|
Элементы: |
|
Критерий для идентификации целевых элементов: |
|
Примечания: |
|
Заданное значение р0 = |
|
Выбранный уровень значимости a = |
|
Объем выборки п = |
|
Пропорция, для которой рассчитывается вероятность неотклонения гипотезы Н0 - р' = |
|
Если критические значения, соответствующие п и р0 для указанного уровня значимости a, неизвестны, они должны быть вычислены по 8.2 (формы В). |
|
Cu,0 = |
|
Определение вероятности неотклонения нулевой гипотезы Н0 - Рa. |
|
Если гипотеза Н0 истинна, вероятность ошибки первого рода равна 1 - Рa. Достигнутый уровень значимости a' равен вероятности ошибки первого рода при р' = р0. |
|
Если альтернативная гипотеза истинна, вероятность ошибки второго рода равна Рa. |
|
|
|
По таблице 3 определяют: |
|
Ф(и'') = |
|
Результаты вычислений: |
|
Рa = 1 - Ф(и'') = |
|
р' = р0 - a'= Ф(и'') = |
|
р' > р0 - b = 1 - Ф(и'') = |
А.3 Двусторонний критерий для Н0: р = р0
|
Характеристика: |
|
Процедура определения: |
|
Элементы: |
|
Критерий для идентификации целевых элементов: |
|
Примечания: |
|
Заданное значение р0 = |
|
Выбранный уровень значимости a = |
|
Объем выборки п = |
|
Пропорция, для которой рассчитывается вероятность неотклонения гипотезы Н0 - р' = |
|
Если критические значения, соответствующие п и р0 для указанного уровня значимости a, неизвестны, они должны быть вычислены по 8.2 (формы В). |
|
Cl,t = Cu,t = |
|
Определение вероятности неотклонения нулевой гипотезы Н0 - Рa. |
|
Если гипотеза Н0 истинна, вероятность ошибки первого рода равна 1 - Рa. Достигнутый уровень значимости a' равен вероятности ошибки первого рода при р' = р0. |
|
Если альтернативная гипотеза истинна, вероятность ошибки второго рода равна Рa. |
|
|
|
|
|
По таблице 3 определяют: |
|
Ф(и') = |
|
Ф(и'') = |
|
Результаты вычислений: |
|
Рa= Ф(и'') - Ф(и') = |
|
Если р' = р0 - a' = 1 - Ф(и'') + Ф(и') = |
|
Если р' # р0 - b = Ф(и'') - Ф(и') = |
Приложение В (справочное)
Примеры заполненных форм
В.1 Формы А
В.1.1 Пример1 - Форма А-2. Односторонний интервал с нижней доверительной границей для пропорции р
|
Характеристика: Наличие видеомагнитофонов в квартирах. |
|||||
|
Процедура определения: Интервью. |
|||||
|
Элементы: Жилые дома в определенном районе. |
|||||
|
Критерий для идентификации целевых элементов: Наличие, по крайней мере, одного видеомагнитофона. |
|||||
|
Примечания: Нет. |
|||||
|
Выбранный уровень доверия 1 - α = 0,95. |
|||||
|
Объем выборки п = 20 |
|||||
|
Число целевых элементов в выборке х = 14. |
|||||
|
Определение границы доверительного интервала |
|||||
|
а) Процедура для п ≤ 30 S |
|||||
|
1) Случай х = 0 £ |
|||||
|
pl,0 = 0 |
|||||
|
2) Случай х > 0 S |
|||||
|
По таблице 2 для известных значений п, Х = п - х и q = (1 - α) определяют: |
|||||
|
T1-α (n, n - x) = 0,508. |
|||||
|
pl,0 = 1- T1-α (n, n - x) = 0,492. |
|||||
|
b) Процедура для п > 30 £ |
|||||
|
1) Случай х = 0 £ |
|||||
|
pl,0 = 0 |
|||||
|
2) Случай х = п £ |
|||||
|
pl,0 = α1/n = |
|||||
|
3) Случай 0 < х < п £ |
|||||
|
По таблице 3 для q = 1 - α определяют u1-α = |
|||||
|
Значение d, соответствующее выбранному уровню доверия, определяют по следующей таблице. |
|||||
|
|
1 - α |
0,90 |
0,95 |
0,99 |
|
|
|
d |
0,411 |
0,677 |
1,353 |
|
|
|
|||||
|
где р* = х/(n + 1). |
|||||
|
Результат (искомый доверительный интервал): |
|||||
|
р £ pl,0 = 0,492. |
|||||
В.1.2 Пример 2 - Форма А-3. Двусторонний доверительный интервал для пропорции р
|
Характеристика: Наличие видеомагнитофонов в квартирах. |
||||||||||
|
Процедура определения: Интервью. |
||||||||||
|
Элементы: Жилые дома в определенном районе. |
||||||||||
|
Критерий для идентификации целевых элементов: Наличие, по крайней мере, одного видеомагнитофона в здании. |
||||||||||
|
Примечания: Нет. |
||||||||||
|
Выбранный уровень доверия 1 - α = 0,99. |
||||||||||
|
Объем выборки п = 90 |
||||||||||
|
Число целевых элементов в выборке х = 19 |
||||||||||
|
Определение границ доверительного интервала |
||||||||||
|
а) Процедура для п ≤ 30 |
||||||||||
|
1) Определение верхней границы доверительного интервала £ |
||||||||||
|
- Случай х = п £ |
||||||||||
|
pи,t = 1 |
||||||||||
|
- Случай х < п £ |
||||||||||
|
По таблице 2 для известных значений п, Х= п - х и q = (1 – α/2) определяют: |
||||||||||
|
pи,t = T1-α/2 (n, x) = |
||||||||||
|
2) Определение нижней границы доверительного интервала: |
||||||||||
|
- Случай х = 0 £ |
||||||||||
|
- Случай х > 0 £ |
||||||||||
|
По таблице 2 для известных значений п, Х= п - х и q = (1 – α/2) определяют: |
||||||||||
|
T1-α/2 (n, n - x) = |
||||||||||
|
pl,t = 1- T1-α/2 (n, n - x) = |
||||||||||
|
b) Процедура для п > 30 S |
||||||||||
|
1) Определение верхней границы доверительного интервала: |
||||||||||
|
- Случай х = 0 £ |
||||||||||
|
pи,t = 1 - (α/2)1/n = |
||||||||||
|
- Случай х = п £ |
||||||||||
|
pи,t = 1 |
||||||||||
|
- Случай 0 < х < п S |
||||||||||
|
По таблице 3 для q = (1 - α/2) определяют u1- α/2 = 2,576. |
||||||||||
|
Значение d, соответствующее выбранному уровню доверия, определяют по следующей таблице. |
||||||||||
|
|
1 - α |
0,90 |
0,95 |
0,99 |
|
|||||
|
|
d |
0,677 |
0,960 |
1,659 |
|
|||||
|
|
||||||||||
|
где р* = (х + 1)/(n + 1). |
||||||||||
|
2) Определение нижней границы доверительного интервала: |
||||||||||
|
- Случай х = 0 £ |
||||||||||
|
pl,t = 0 |
||||||||||
|
- Случай х = п £ |
||||||||||
|
pl,t = (α/2)1/n = |
||||||||||
|
- Случай 0 < х < п S |
||||||||||
|
По таблице 3 для q = (1 - α/2) определяют u1- α/2 = 2,576. |
||||||||||
|
Значение d, соответствующее выбранному уровню доверия, определяют по следующей таблице. |
||||||||||
|
|
1 - α |
0,90 |
0,95 |
0,99 |
|
|||||
|
|
d |
0,677 |
0,960 |
1,659 |
|
|||||
|
|
||||||||||
|
где р* = х/(n + 1). |
||||||||||
|
Результаты (искомый доверительный интервал): pl, t = 0,111; pu,t = 0,341; pl, t ≤ p ≤ pu,t |
||||||||||
В.2 Формы В
В.2.1 Пример 1 - Форма В-2. Сравнение пропорции р с заданным значением р0 для одностороннего критерия с Н0: р £ р0
|
Характеристика: Наличие видеомагнитофонов в квартирах. Процедура определения: Интервью. Элементы: Жилые дома в определенном районе. Критерий для идентификации целевых элементов: Наличие, по крайней мере, одного видеомагнитофона. Примечания: Нет. |
|
Заданное значение р0 = 0,48 Выбранный уровень значимости a = 0,05 Объем выборки п = 20 Число целевых элементов в выборке х = 14 |
|
Процедура проверки гипотез |
|
I Критические значения известны (см. 7.2.1) Си,0 = Гипотезу Н0 отклоняют, если х > Си,0. В противном случае гипотезу не отклоняют. |
|
II Критические значения неизвестны S |
|
а) Случай х £ р0п £ |
|
Гипотезу Н0 не отклоняют. |
|
b) Случай х > р0п S |
|
1) Процедура для п £ 30 S |
|
По 8.1.2 (форма А-2) определяют одностороннюю нижнюю доверительную границу для п, х и уровня доверия (1 - a) |
|
pl, 0 = 0,492. |
|
Гипотезу Н0 отклоняют, если pl, 0 > р0, в противном случае гипотезу не отклоняют. |
|
2) Процедура для п > 30 £ |
|
- Случай х = п £ |
|
pl, 0 = a1/n = [см. 8.1.2 b) 2)]. |
|
Гипотезу Н0 отклоняют, если pl, 0 > р0, в противном случае гипотезу не отклоняют. |
|
- Случай 0 < х < п £ |
|
По таблице 3 для q = (1 - a) определяют u1- α = |
|
|
|
Гипотезу Н0 отклоняют, если и2 > u1- α, в противном случае гипотезу не отклоняют. |
|
Результат проверки гипотезы: |
|
Гипотеза Н0 отклонена S |
|
Гипотеза Н0 не отклонена £ |
|
Определение критических значений |
|
Си,0 - наибольшее целое число х, для которого процедура проверки гипотез по форме В-2 (II) не ведет к отклонению нулевой гипотезы. Значение Си,0 определяют методом итераций путем повторного применения формы В-2 (II) с различными значениями х, пока не будут найдены такие два значения, которые отличаются друг от друга на 1, и при этом одно из значений приводит к отклонению нулевой гипотезы Н0, а другое значение приводит к неотклонению нулевой гипотезы Н01). Начальное значение хстарт может быть получено следующим образом. |
|
В качестве х*2) принимают значение пр0, округленное до ближайшего целого числа, =10. pu,0|x = x* = 0,699 (pu,0|x = x* определяют по 8.1.1, форма А-1) хстарт = значение npu,0|x = x*, округленное до ближайшего целого числа, и равно 14. |
|
Интерпретация результатов проверки гипотез по форме В-2 (II): |
|
для х £ Си,0 = 13 гипотезу Н0 не отклоняют; |
|
для х ³ Си,0 + 1 = 14 гипотезу Н0 отклоняют. |
|
Результат проверки гипотез: |
|
Си,0 = 13 |
|
1) Критическое значение (или одно из критических значений) может не существовать для некоторых значений р0 и/или для очень маленьких объемов выборок п. |
|
2) х* - вспомогательная величина для нахождения хстарт |
В.2.2 Пример 2 - Форма В-3. Сравнение пропорции р с заданным значением р0 для двустороннего критерия с Н0: р = р0
|
Характеристика: Наличие видеомагнитофонов в квартирах. |
|
Процедура определения: Интервью. |
|
Элементы: Жилые дома в определенном районе. |
|
Критерий для идентификации целевых элементов: Наличие, по крайней мере, одного видеомагнитофона. |
|
Примечания: Нет. |
|
Заданное значение р0 = 0,33 Выбранный уровень значимости a = 0,01. Объем выборки п = 90 Число целевых элементов в выборке х = 19. |
|
Процедура проверки гипотез |
|
I Критические значения известны (см. 7.2.1) £ Cl,t = Cu,t = Гипотезу Н0 отклоняют, если х < Cl,t или х > Cu,t, в противном случае гипотезу не отклоняют. |
|
II Критические значения неизвестны S |
|
а) Процедура для п £ 30 £ |
|
По 8.1.3 (форма А-3) определяют двусторонние доверительные границы для п, х и уровня доверия (1 - a): pl,t = pu,t = Гипотезу Н0 отклоняют, если pl,t > р0 или pu,t < р0, в противном случае гипотезу не отклоняют. |
|
b) Процедура для п > 30 S |
|
1) Случай х = 0 £ pu,t = 1 - (a/2)1/n = Гипотезу Н0 отклоняют, если pu,t < р0, в противном случае гипотезу не отклоняют. |
|
2) Случай х = п £ pl,t = (a/2)1/n = Гипотезу Н0 отклоняют, если pl,t > р0, в противном случае гипотезу не отклоняют. |
|
3) Случай 0 < х < п S По таблице 3 для q = (1 - α/2) определяют u1- α/2 = 2,576
|
|
Гипотезу Н0 отклоняют, если u1 > u1- α/2 или u2 > u1- α/2 в противном случае гипотезу не отклоняют. |
|
Результат проверки гипотез: |
|
Гипотеза Н0 отклонена £ |
|
Гипотеза Н0 не отклонена S |
|
Определение критических значений Cl,t - наименьшее неотрицательное целое число х, а Си,t - наибольшее целое число х, для которого проверка гипотез по форме В-3 (II) не ведет к отклонению Н0. Значения Cl,t и Си,t определяют методом итераций путем повторного применения формы В-3 (II) с различными значениями х до тех пор, пока не будут определены такие две пары значений, у которых значения в каждой паре отличаются друг от друга на 1, и при этом одно из значений приводит к отклонению нулевой гипотезы Н0, а другое значение приводит к неотклонению нулевой гипотезы Н01). Начальное значение хстарт может быть получено следующим образом. |
|
В качестве х*2) определяют значение пр0, округленное до ближайшего целого числа, х* = 30 pi,t|x = x* = 0,210; pu,t|x = x* = 0,473. pi,t|x = x* и pu,t|x = x* определяют по 8.1.3 (форма А-3); хстарт (нижнее) = значение npi,t|x = x*, округленное до ближайшего целого числа, и равно 19. хстарт (верхнее) = значение пpu,t|x = x*, округленное до ближайшего целого числа, и равно 43. |
|
Интерпретация результатов проверки гипотез по форме В-3 (II): для х £ Cl,t - 1 = 18 гипотезу Н0 отклоняют; для х = Cl,t = 19 и х = Си,t = 42 гипотезу Н0 не отклоняют; для х ³ Си t + 1 = 43 гипотезу Н0 отклоняют. |
|
Результаты проверки гипотез: Cl,t = 19; Си,t = 42. |
|
1) Критическое значение (или одно из критических значений) может не существовать для некоторых значений р0 и/или для очень маленьких объемов выборок п. |
|
2) х* - вспомогательная величина для нахождения хстарт |
В.3 Формы С
В.3.1 Пример 1 - Форма С-1. Сравнение двух пропорций для одностороннего критерия Н0: р1 ³ р2
|
Характеристика: Наличие видеомагнитофонов в квартирах. |
|
Процедура определения: Интервью. |
|
Элементы: |
|
1) жилые дома в области А; |
|
2) жилые дома в области В. |
|
Критерий для идентификации целевых элементов: Наличие, по крайней мере, одного видеомагнитофона в зданиях. |
|
Примечания: Нет. |
|
Выбранный уровень значимости a = 0,05. Объем выборки 1: п1 = 10. Объем выборки 2: п2 = 15. Число целевых элементов в выборке 1: х1 = 8. Число целевых элементов в выборке 2: х2 = 13. |
|
Проверка для тривиального случая |
|
|
|
Неравенство является истинным £ |
|
Неравенство не является истинным S |
|
Если неравенство является истинным, нулевую гипотезу не отклоняют и результат проверки гипотез может быть объявлен немедленно. В противном случае проводят следующую процедуру, которая может привести к отклонению или к неотклонению гипотезы Н0. |
|
Процедура проверки гипотез для нетривиальных случаев Если, по крайней мере, одно из четырех значений п1, п2, (х1 + х2), (п1 + п2 - х1 - х2) меньше или равно (п1 + п2)/4, то применяют биномиальную аппроксимацию, приведенную в I настоящей формы; в противном случае применяют нормальную аппроксимацию, приведенную в II настоящей формы. Однако даже если вышеупомянутое условие выполнено, можно применять нормальную аппроксимацию, если выполнены два следующих условия: - при применении биномиальной аппроксимации в таблице 4 F-распределения необходимо использовать интерполяцию; - п1 и п2 или (х1 + х2) и (п1 + п2 - х1 - х2) попарно являются величинами одного порядка. |
|
Решение: |
|
Должна применяться биномиальная аппроксимация (продолжить с I) S |
|
Должна применяться нормальная аппроксимация (продолжить с II) £ |
|
I Биномиальная аппроксимация |
|
Определение величин: К1, К2, h1, h2 |
|
Если [п2 < п1 и п2 < (х1 + х2)] или [(п1 + п2 - х1 - х2) < п1 и (п1 + п2 - х1 - х2) < (х1 + х2)], искомые величины определяют следующим образом: |
|
h1 = п2 = 15; |
|
h2 = п1 = 10; |
|
К1 = п2 - х2 = 2; |
|
К2 = п1 - х1 = 2. |
|
В противном случае: |
|
h1 = п1 = |
|
h2 = п2 = |
|
К1 = х1 = |
|
К2 = х2 = |
|
Вычисление статистики и определение значений по таблице 4 |
|
а) Случай h1 £ К1+ К2 £ |
|
|
|
Числа степеней свободы F-распределения: |
|
f1 = 2(К1 + 1) = |
|
f2 = 2(h1 - К1) = |
|
По таблице 4 для q = (1 - a), f1 и f2 (при необходимости применяют интерполяцию) определяют: |
|
F1 - a( f1, f2) = |
|
b) Случай h1 > К1+ К2 S |
|
|
|
Число степеней свободы F-распределения: |
|
f1 = 2(К1 + 1) = 6; |
|
f2 = 2К2 = 4. |
|
По таблице 4 для q = (1 - a), f1 и f2 (при необходимости применяют интерполяцию) определяют: |
|
F1 - a( f1, f2) = 6,16. |
|
Заключение в нетривиальном случае для биномиальной аппроксимации: |
|
Гипотезу Н0 отклоняют, если F2 ³ F1-a(f1, f2), в противном случае гипотезу Н0 не отклоняют. |
|
II Нормальная аппроксимация |
|
Вычисление статистики и определение значений по таблице 3 |
|
|
|
По таблице 3 для q = (1 - a) определяют u1-a = |
|
Заключение в нетривиальном случае для нормальной аппроксимации: |
|
Гипотезу Н0 отклоняют, если z2 ³ u1-, в противном случае гипотезу Н0 не отклоняют. |
|
Результат проверки гипотез: |
|
Гипотеза Н0 отклонена £ |
|
Гипотеза Н0 не отклонена S |
В.3.2 Пример 2 - Форма С-3. Сравнение двух пропорций для двустороннего критерия Н0: р1 = р2
|
Характеристика: |
|
1) наличие видеомагнитофонов марки А в квартирах; |
|
2) наличие видеомагнитофонов марки В в квартирах. |
|
Процедура определения: Интервью. |
|
Элементы: Жилые дома одной определенной области. |
|
Критерий для идентификации целевых элементов: |
|
1) наличие, по крайней мере, одного видеомагнитофона марки А; |
|
2) наличие, по крайней мере, одного видеомагнитофона марки В. |
|
Примечания: Нет. |
|
Выбранный уровень значимости a = 0,01. |
|
Объем выборки 1: п1 = 95. |
|
Объем выборки 2: п2 = 95. |
|
Число целевых элементов в выборке 1: х1 = 41. |
|
Число целевых элементов в выборке 2: х2 = 21. |
|
Проверка гипотез для тривиального случая |
|
|
|
Неравенство является истинным £ |
|
Неравенство не является истинным S |
|
Если неравенство является истинным, гипотезу не отклоняют и результат проверки гипотезы может быть объявлен немедленно. В противном случае проводят следующую процедуру, которая может привести к отклонению или к неотклонению гипотезы Н0. |
|
Проверка гипотез для нетривиальных случаев |
|
Если, по крайней мере, одно из четырех значений п1, п2, (х1 + х2), (п1 + п2 - х1 - х2) меньше или равно (п1 + п2)/4, то применяют биномиальную аппроксимацию, приведенную в I настоящей формы; в противном случае применяют нормальную аппроксимацию, приведенную в II настоящей формы. Однако даже если вышеупомянутое условие выполнено, можно применять нормальную аппроксимацию, если выполнены два следующих условия: |
|
- при применении биномиальной аппроксимации в таблице 4 F-распределения необходимо использовать интерполяцию; |
|
- п1 и п2 или (х1 + х2) и (п1 + п2 - х1 - х2) попарно являются величинами одного порядка. |
|
Решение: |
|
Должна применяться биномиальная аппроксимация (продолжить I) £ |
|
Должна применяться нормальная аппроксимация (продолжить II) S |
|
I Биномиальная аппроксимация |
|
Определение величин: К1, К2, h1, h2 |
|
Если [п2 < п1 и п2 < (х1 + х2)] или [(п1 + п2 - х1 - х2) < п1 и (п1 + п2 - х1 - х2) < (х1 + х2)], искомые величины определяют следующим образом: |
|
h1 = п2 = |
|
h2 = п1 = |
|
К1 = п2 - х2 = |
|
К2 = п1 - х1 = |
|
В противном случае: |
|
h1 = п1 = |
|
h2 = п2 = |
|
К1 = х1 = |
|
К2 = х2 = |
|
Вычисление статистики и определение значений по таблице 4 |
|
а) Случай h1 £ К1 + К2 £ |
|
1) Случай |
|
Значения F1, f1 и f2 определяют по 8.3.2 (форма С-2) |
|
|
|
Числа степеней свободы F-распределения: |
|
f1 = 2(h1 - К1 + 1) = |
|
f2 = 2К1 = |
|
По таблице 4 для q = (1 - a/2), f1 и f2 (при необходимости применяют интерполяцию) определяют: |
|
F1-a/2(f1, f2) = |
|
2)
Случай |
|
Значения F2, f1 и f2 определяют по 8.3.1 (форма С-1) |
|
|
|
Числа степеней свободы F-распределения: |
|
f1 = 2(К1 + 1) = |
|
f2 = 2(h1 - К1) = |
|
По таблице 4 для q = (1 - a), f1 и f2 (при необходимости применяют интерполяцию) определяют: |
|
F1 - a( f1, f2) = |
|
b) Случай h1 > К1 + К2 £ |
|
1) Случай |
|
Значения F1, f1 и f2 определяют по 8.3.2 (форма С-2) |
|
|
|
Число степеней свободы F-распределения: |
|
f1 = 2(К1 + 1) = |
|
f2 = 2К2 = |
|
По таблице 4 для q = (1 - a/2), f1 и f2 (при необходимости применяют интерполяцию) определяют: |
|
F1-a/2(f1, f2) = |
|
2) Случай |
|
Значения F2, f1 и f2 определяют по 8.3.1 (форма С-1). |
|
|
|
Число степеней свободы F-распределения: |
|
f1 = 2(К1 + 1) = |
|
f2 = 2К2 = |
|
По таблице 4 для q = (1 - a/2), f1 и f2 (при необходимости применяют интерполяцию) определяют: |
|
F1-a/2(f1, f2) = |
|
Заключение в нетривиальном случае для биномиальной аппроксимации |
|
Гипотезу Н0 отклоняют, если: |
|
F1 ³
F1-a/2(f1, f2) в случае |
|
или |
|
F2
³
F1-a/2(f1, f2) в
случае |
|
в противном случае гипотезу Н0 не отклоняют. |
|
II Нормальная аппроксимация Вычисление статистики и определение значений по таблице 3 |
|
а) Случай |
|
Значение z1 определяют по 8.3.2 (форма С-2) |
|
|
|
По таблице 3 для q = (1 - a/2) определяют |
|
u1-a/2 = 2,576. |
|
b) Случай |
|
Значение z2 определяют по 8.3.1 (форма С-1) |
|
|
|
По таблице 3 для q = (1 - a/2) определяют |
|
u1-a/2 = |
|
Заключение в нетривиальном случае для нормальной аппроксимации Гипотезу Н0 отклоняют, если: |
|
z1 ³
u1-a/2 в случае |
|
или |
|
z2 ³ u1-a/2 в случае |
|
в противном случае гипотезу Н0 не отклоняют. |
|
Результат проверки гипотез: |
|
Гипотеза Н0 отклонена S |
|
Гипотеза Н0 не отклонена £ |
Приложение С (справочное)
Сведения о соответствии межгосударственных стандартов ссылочным международным стандартам
|
Обозначение ссылочного международного стандарта |
Обозначение и наименование соответствующего межгосударственного стандарта |
|
ИСО 3534-1 : 1993 |
* |
|
* Соответствующий межгосударственный стандарт отсутствует. На территории Российской Федерации действует ГОСТ Р 50779.10-2000 (ИСО 3534-1-93). |
|
Приложение D (справочное)
Библиография
[1] WALTERS, D.E., In defense of the arc sine approximation. The Statistical. 28, 1979, pp. 219-222
[2] HASEMAN, J.K., Exact sample sizes for use with the Fisher-Irwin test for 2 x 2 tables. Biometrics, 34 (1978), pp. 106-109
Ключевые слова: статистика, статистический анализ, статистическая проверка гипотез, критерий проверки гипотез, статистический доверительный интервал, доверительные границы
